ABEJAでResearcherしている白川です。

今回ご紹介するのは、Poincaré Embeddings [1]という手法です。その内容に驚愕し、個人的に調べたり実装したり勉強会でお話したりしていたところ、最近運良く自分の実装をredditで取り上げてもらえたので、これを機にその驚愕の内容を共有できればと思います。正直、自分の中ではまだ煮詰まりきっていない技術なので、現況の共有はしますが、ところどころ私の憶測や展望、期待が入り混じっていることをご容赦ください。

Poincaré Embeddingsは大雑把に言えばword2vecを異空間で実現する技術で、双曲空間（Hyperbolic Space）という、おなじみのEuclide空間（2点$x,y$の間の距離を$\sqrt{(x_1 - y_1)^2 + (x_2 - y_2)^2 + ... + (x_d - y_d)^2}$で測るいつもの空間）とは異なる空間でデータを表現します。それにより、従来手法（word2vecのようにEuclide空間へ埋め込む手法）では200次元くらいのベクター表現を要していたケースで、なんと5次元で遥かに高い精度を達成することに成功しています。

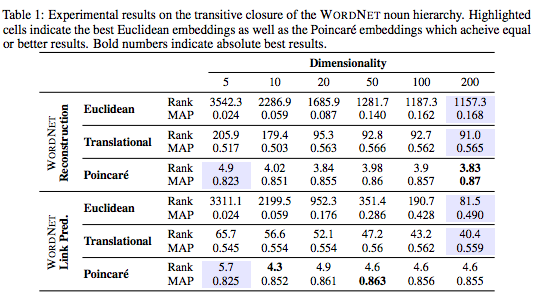f:id:daynap1204:20170827142406p:plain Poincaré Embeddingsによる埋め込み精度の向上（[1]から引用）

Poincaré空間に埋め込むことによるメリットを列挙しておきます。

Euclide空間への埋め込みに比べて、空間をexponentialに効率よく利用できる
それにより、十分精度の埋め込みを低次元で実現できる
データのもつ階層構造を自動的に抽出できる
実装が簡単（ちょっとした補正をするだけです）
アイデアがわかりやすい
リーマン多様体上での機械学習の取っ掛かりとしてよい

この手法、アイデアは簡単ですがとても可能性を感じます（リーマン多様体上の機械学習とかは昔からちょいちょいあるので、やっと実用段階に来たかという感が強いですが）。論文を読むと数学的なバックグラウンドが一見必要に見えますが、やってることは単純ですので、本記事でその雰囲気を噛み砕いてお伝えできればと思います。

なお、私はグラフ構造をDeep Learningで表現したり、グラフ構造を使って課題を解決することに興味を持っているのですが、本手法をそういったケースにうまく使えないか模索しています。とにかく、シンプルなアイデアなのでいろいろ想像が膨らんで楽しいです！

以下、勉強会で使ったslideもあるので、合わせてご参照ください。本稿で説明しきれていない内容もちょいちょい盛り込んであります。

Poincare embeddings for Learning Hierarchical Representations from Tatsuya Shirakawa

www.slideshare.net

また、私の実装は下記にあります。本稿で紹介する実験の一部も再現できるので、ご興味あればお試しください。IssueやPRも大歓迎です。

github.com

まずはword2vecから復習していきましょう。

word2vecの復習

word2vecやskipgramをよくご存じの方は本節は飛ばしても大丈夫です。

word2vec[2]はテキスト中の単語の表現ベクターを求めるツールで、skipgramとcbow[3,4]という2つのモデルが実装されています。

もともと、Yoshua Bengioらにより、Deep Neural Networksを使って単語の表現ベクター（分散表現）を求めるという論文[5]が2001年(!)に出されていたのですが、この論文では、単語の表現ベクターをDeep Neural Networksを用いて求めるという仕組みになっていました。

Tomas Mikolovによるskipgram/cbowの発見の貢献は、Deep Neural Networksのような複雑でパワフルなモデルを使わなくとも、単語の「表現ベクター表」を直接最適化していけば良いことを実証したことにあります（冷静に考えれば表の最適化だけでよいことはわかります）。

さらにTomas Mikolovらは、Negative Samplingという仕組みを導入し、圧倒的な計算効率の向上も実現しています[6]。ここにおいて、NLP界隈でのword2vec祭が始まりました。よいモデルとよい実装がちゃんと公開されるというのは素晴らしいことですね！ちなみに私はシンプルで強力なword2vecが大好きです。

さて、word2vecですが、ここではNegative Samplingつきのskipgram（SGNS）の方だけ説明します（cbowもちょっとモデルが違いますがノリは一緒です）。 SGNSは、非常に単純なモデルで、単語の表現ベクター表を用意しておいて

文中に近接して出て来る単語対（positive samples）の表現ベクターは内積が大きい
乱択された単語対（negative samples）の表現ベクターは内積が小さい

となるように最適化を行います。具体的には、単語 $i$ の表現ベクターを $v_i$ とするとき $V={\{v_i\}}_{i \in I}$ が表現ベクター表ですね）、下記の目的関数を最大化します。

$\text{maximize}_{ \{v_i \}_i } \ \ \mathbb{E}_{(i,j) \sim P(i,j)} \Bigl[ \log \sigma ( \langle v_i, v_j \rangle ) \Bigr] + k \ \mathbb{E}_{(i,j) \sim P(i)P(j)} \Bigl[ \log 1-\sigma (\langle v_i, v_j \rangle) \Bigr]$

ここで、$\langle v_i, v_j \rangle$は単語$i,j$の表現ベクターの内積です。$P(i,j)$は単語対$(i,j)$が近接して現れる確率分布（下図の場合、注目している語onの左右に2単語以内に現れる単語を近接語としています）を表し、$P(i)$は単語$i$単独の頻度分布（unigram分布）です。また、$k$はpotive samplesとnegative samplesのバランスをコントロールする非負定数で（理論的には$k=1$が理想ですが、$k=5,10,20$などの値が実用上用いられます）、関数$\sigma(x)=1/(1+\exp(-x))$はシグモイド関数です（$P(i)$を3/4乗したりという細かいチューニングが本当はあるのですが、本質的でないので無視しています）。

難しいことを抜きにしたら、positive samplesの出現確率を増加させ、negative samplesの出現確率を低下させるように単語の表現ベクターを求めていることになります。

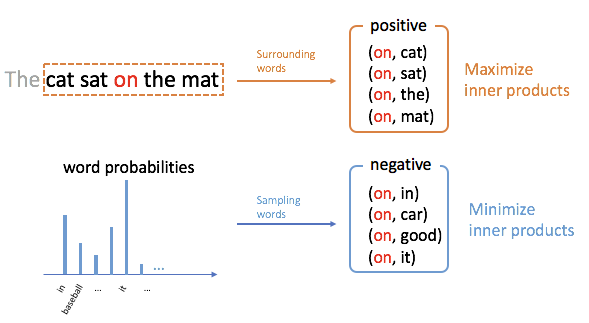f:id:daynap1204:20170827155338p:plain SkipGram with Negative Sampling (SGNS)

なお、SGNSはpointwise mutual information（PMI）を要素値にとる行列の分解になることが知られています（GANsのオリジナル論文のdiscriminatorの収束証明と同様の議論で容易に示せます）。

$$ \langle v_i, v_j \rangle = PMI(i,j) = log \frac{P(i,j)}{P(i)P(j)} $$

SGNSの素晴らしい点は、その計算効率です。テキストデータの上に窓（上図の左上の点線窓）を滑らせていきながら注目語（上図ならon）と周辺語（同cat, sat, the, mat）を取得していき（positive samples）、その一方で単語の頻度分布から単語をサンプリング（negative samples）してくれば、あとは確率的勾配降下法により容易に最適化できます。さらに、これにより得られる単語の表現ベクターは、よく知られているような正則性をもつことが実験的に知られています（linguistic regularity）。king-man = queen-womanというやつですね。

f:id:daynap1204:20170827161023p:plain

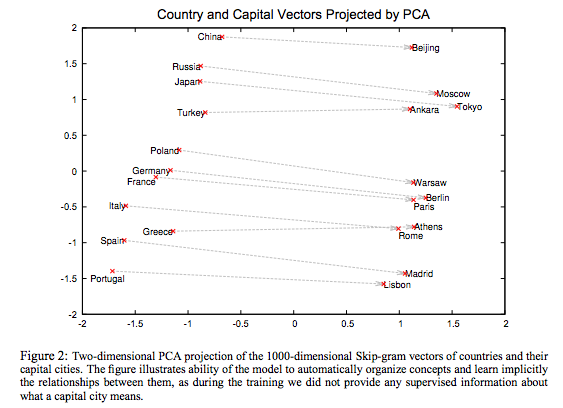
[6]より引用

SGNSですが、適用先はテキストデータだけにとどまりません。ここではグラフ構造への適用例として、LINE（Large-scale Information Network Embedding）[7]という手法を紹介します。なお、ここでグラフへの適用を紹介するのは、私の趣味もありますが、本題のpoincaré embeddingもグラフ構造（実際は木構造）に関係するからというのもあります。word2vecはグラフ構造へ何も考えずそのまま適用できるのになかなか日の目を見ないという状況を改善したいという気持ちもあります（もちろん常識的に適用している方もたくさんおられると思います）。

LINE - グラフへのSGNSの適用

LINEはグラフへSGNSを適用する手法です。具体的には、下記の対応関係にあります。

対象	LINE	SGNS
埋め込まれるもの	ノード	単語
P(i)	ノードの次数に比例	単語の出現頻度に比例
P(i,j)	グラフのエッジからの一様分布	窓から一様サンプリング

すなわち、下記のような学習になります。

グラフからエッジを一様サンプリングして単語対を生成（positve samples）
ノードを次数に比例する確率で2つサンプリングすることでノード対を生成（negative samples）

最適化するのもSGNSと同じ目的関数です。

$ \text{maximize}_{ \{v_i \}_i } \ \ \mathbb{E}_{(i,j) \sim P(i,j)} \Bigl[ \log \sigma (\langle v_i, v_j \rangle ) \Bigr] + k \ \mathbb{E}_{(i,j) \sim P(i)P(j)} \Bigl[ \log 1-\sigma (\langle v_i, v_j \rangle ) \Bigr]$

グラフにもそのまま適用できたのは、SGNSのシンプルさのおかげですね。

Poincaré Embeddings

ここからが本題です。SGNSはシンプルで素晴らしい。計算効率も非常に良い。これ以上言うことはないのではないかと思っていましたが、Poincaré Embeddingsはそこに待ったをかけました。

その埋め込み、最良ですか？

SGNSでは、二つの単語$i,j$の表現ベクター$v_i, v_j$をとり、その内積

$$ \langle v_i, v_j \rangle $$

でそれらの単語の共起の度合いを測りました（これが大きい方が共起しやすい）。

でもそれより良い測り方はないのでしょうか？

Poincaré Embeddings[1]では、Euclide空間よりも空間効率の良い双曲空間という歪んだ空間へデータ（ノードや単語）を埋め込み、その空間でそれらのデータ間の距離を測ることで、はるかに効率的な表現ベクターを獲得することに成功しました。

内積$\langle u,v \rangle$は $$ \langle u,v \rangle = ({\Vert u + v \Vert}^2 - {\Vert u \Vert}^2 + {\Vert v \Vert}^2)/2 $$ を満たすので、本質的にEulide空間における距離の測り方に依存しています。したがって、SGNSはEuclide空間への埋め込みモデルと考えることができます。 Deep Learningで扱われるたいていのモデルはEuclide空間で構成されていると考えて差し支えないと思います（もちろん例外はあります）。

Poincaré Embeddingsの場合、Euclide空間ではなく、双曲空間（Hyperbolic Space）で埋め込みを構成します。双曲空間ではEuclide空間と同様、各点はベクターとして表現されますが、Euclide空間とは異なり空間に歪みがあり、2点間の距離の測られ方が異なります。そのため、この歪みを利用することでEuclide空間よりも効率的で個性的な埋め込みが可能になります（要はEuclide空間はフラットすぎたんですね）。

双曲空間についてさらっておきます。

双曲空間（hyperbolic space）

双曲空間は数学的には非常に由緒正しい空間です。深掘りすると議論が尽きないので、ここでは美味しいところだけつまみ食いしましょう。詳細については、wikipedia[8]や論文[9]を参照してください。書籍であれば、以下の本が非常にわかりやすく書かれています。

双曲幾何 (現代数学への入門)

作者: 深谷賢治
出版社/メーカー: 岩波書店
発売日: 2004/09/07
メディア: 単行本
クリック: 6回
この商品を含むブログ (2件) を見る

私は読んでいないですが、書店でちら見した感じでは、最近出た下記の本にも双曲空間が易しく解説されていました。

曲がった空間の幾何学現代の科学を支える非ユークリッド幾何とは (ブルーバックス)

作者: 宮岡礼子
出版社/メーカー: 講談社
発売日: 2017/07/19
メディア: 新書
この商品を含むブログ (1件) を見る

双曲空間にはいくつかの構成方法（モデル）がありますが、ここでは、オリジナル論文に従ってPoincaré Ball (Poincaré Disk) モデルを採用します。Poincaré Ballモデルでは、データは$d$次元の単位球$\mathbf{B}^d = \{x \in \mathbb{R}^d | \Vert x \Vert < 1 \}$ 内に表現されます。Poincaré Ballモデルの場合、この単位球$\mathbf{B}^d$の周縁部（$\Vert x \Vert = 1$）に近づくに従って解像度が加速度的に高くなるようになっていて（外側に行くほど空間が爆発的に広がっているイメージです）、これが表現の効率性を生み出しています。

双曲空間については、エッシャーによる描画があります。

f:id:daynap1204:20170827165827j:plain

M.C. Escher, Circle Limit III, 1959

外側に行くほど空間が密に詰まっているのがわかると思います（逆に見れば、外側ほど空間が拡がっています）。

数学的にはこの空間の拡がり方の増加は、下記のように表されます。

$$ g_x = \Biggl(\frac{2}{1-{\Vert x \Vert }^2 } \Biggr)^2 g^E $$

この式の意味ですが、$g_x$がPoincaré Disc上での物差し（metric）、$g^E$がEuclide空間の物差しを表します。Poincaré Ball上の点$x$における空間の拡がり方は、同じ点のEuclide空間における拡がり方に比べて、$2/(1-{\Vert x \Vert}^2)$倍であることを表します。$\Vert x \Vert$が1に近づけば近づくほどこの倍数は大きくなっていくので、Poincaré Ballの周縁部へ行くほど空間が拡大されていくことになります。

では、Poincaré Ballの2点$x,y$の間の距離はどのようになるのでしょうか？数学的には、このような歪んだ空間における2点間の距離は、測地線（geodesic）という2点を結ぶ最短経路の長さで定義されます。Euclide空間における2点間の距離はその2点を結ぶ直線の長さで定義されましたが、測地線はEuclide空間における距離の概念を歪んだ空間（多様体）へ拡張したものです。

Poincaré Ballでは場所ごとに物差しの長さ異なるため、点$x$から点$y$へ至る道それぞれの途上で物差しは変化し続けることになります。そのため、それらの道のうちの最短のもの（測地線）がどんなものでその長さがいくらかを特定したり計算したりするのは難しそうな気がしますが、幸いなことにPoincaré Ballの場合、

2点$x,y$を結ぶ測地線は常にその2点を通り、単位球に直行する円弧になる
測地線の長さは明示的に計算可能で$d(x,y) = arccosh \Bigl(1 + 2 \frac{{\Vert x - y \Vert}^2}{(1-{\Vert x \Vert}^2)(1-{\Vert y \Vert}^2)} \Bigr)$

となることが知られています。ここで、$arccosh(\gamma)=\log \bigl(\gamma + \sqrt{\gamma-1}\sqrt{\gamma+1} \bigr)$は逆双曲線余弦関数と呼ばれる関数です。

f:id:daynap1204:20170827231134p:plain

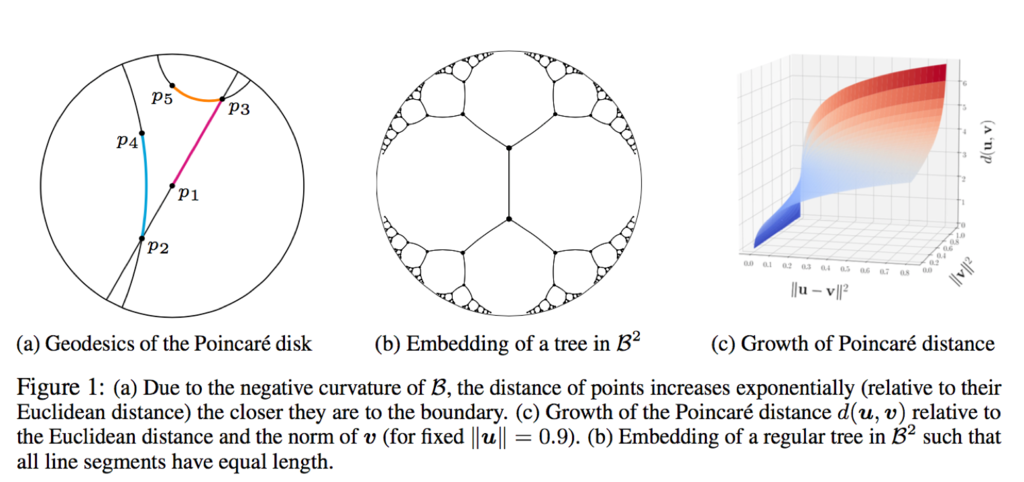
[1]より引用

これだけでも嬉しいのですが、それだけでは終わりません。双曲空間には木構造を自然な形で埋め込むことができるという特殊な性質が知られており、木構造を構成するノード間の距離（家系図で言うところの1親等、2親等というやつです）を保つように、適当な次元の双極空間へ埋め込むことができます[9]。雰囲気だけ理解することにすれば、この埋め込みは木のルートに近いノードをPoincaré Ballの中心近くに、リーフに近いノードをPoincaré Ballの周縁部の近くに配置します（上図の(b)）。

この性質により、Poncaré Ballへ埋め込んだときに中心近くに配置されるデータはより抽象度が高く、周縁部に配置されるデータは具象度が高くなることが期待されます（あとで見るように、実際にそうなるところが驚愕すべき点です）。

勢いで書いてしまったので整理します。

双曲空間は数学的に由緒正しい空間
双曲空間はPoincaré Ballモデルを採用することで、単位球内に表現することができる

さらに、Poincaré Ballモデルは

単位球の原点から周縁部に行くにつれ、空間が加速度的に拡がっていき、空間効率よくデータを埋め込むことができる
2点間の距離は明示的に計算できる
階層構造が末端ほど周縁部に配置されるように自然に埋め込まれることが知られている。

という素晴らしい性質を持ちます。

Poincaré Embeddingsの構成

Poincaré EmbeddingsはPoincaré Ballへデータを埋め込む手法です。skipgramではデータ対$(i,j)$の間の類似度を内積$\langle v_i, v_j \rangle$で表していましたが、Poincaré Embeddingsのオリジナル論文では、これを2点間の距離の符号を反転したもの$-d(v_i,v_j)$で表します。内積で表していたものを距離で表すことにしたので、厳密にはskipgramとPoincaré Embeddingは対応が崩れていますが、ここでは目を瞑っておきます（あとで触れるように、双曲空間で内積相当のものを定義して利用している論文も出ています[10]）。

Poincaré Embeddingsをskipgramと同様に学習する場合、

共起するデータ対（positive samples）に対しては距離を小さく
乱択されたデータ対（negative samples）に対しては距離を大きく

という具合に最適化を行います。ただし、距離関数が非負値な関係上、距離$d(v_i,v_j)$をそのまま使わずに、負値もとれるように $$ \frac{d(v_i, v_j) - r}{t}$$ というような補正を入れます（$r,t$はハイパーパラメータです）。ちょっと歯がゆい感じですが、致し方なし。より良い類似度/非類似度関数の定義はfuture worksを待ちましょう。

最適化はRiemannian SGDという歪んだ空間で実行可能なSGD（確率的勾配降下法）により行いますが、こちらの説明は下記のスライド1枚にかえさせていただきます。要点は簡単で、勾配降下する際に、物差しの長さ分の補正をするだけです。

f:id:daynap1204:20170828013331p:plain

オリジナル論文[1]における実験結果

お待ちかねの実験結果です。2種類の実験をしています。

WordNet の名詞の階層構造の埋め込み
グラフのリンク予測

それぞれ見ていきましょう。細かい詳細は割愛していますので、必要であればオリジナル論文[1]を参照してください。

WordNet の名詞の階層構造の埋め込み

こちらは最初に挙げた私の実装でも再現できるようにしてあります。実行方法の詳細はREADMEをご覧ください。

WordNet[10]は英語の概念辞書です。オリジナル論文では、ここから名詞のみを抽出し、その概念上の上位・下位関係を列挙したものをデータセットとしています（例えば犬は哺乳類なので、上位概念が哺乳類、下位概念が犬という具合です）。具体的には

下位語	上位語
apple_jelly.n.01	confiture.n.01
telephone_system.n.01	physical_entity.n.01
organizer.n.02	causal_agent.n.01
utmost.n.01	extent.n.02
tael.n.01	abstraction.n.06
financial_institution.n.01	organization.n.01
uruguayan.n.01	whole.n.02
holocentrus_ascensionis.n.01	vertebrate.n.01
bell_metal.n.01	substance.n.01
takeoff.n.02	happening.n.01
...	...

という感じのデータになると想像されます（論文に書いてなかったので私は実験結果の数値をもとに、想像しながら合わせ込みました…）。このデータは名詞対の並びになっていて、左側に下位の語が、右側に上位の語が来るようにしてあります。".n"はその語が名詞であることを表し、".01"や".02"といった数字は、同じ綴りでも意味が異なる語を区別するために付けられています。

この1行を1 positive sampleとし、negative samplesはこのデータ中の単語の出現頻度に比例した確率で2単語乱択することにより生成します。

上記データに対して、下記のような関数の最大化を行います。

$$ \mathcal{L}(\Theta) = \sum_{(i, j)\in \mathcal{D}} \log \frac{ \exp(-d(v_i, v_j))}{\sum_{j' \in \mathcal{N}(i)} \exp(-d(v_i, v_{j'}))}$$

ここで、$\Theta$はこのモデルのパラメータ全体を表し、$\mathcal{N}(i)$は、データ$i$に対して生成された$j$のnegative samplesで、基本的には出現頻度に比例した乱択で生成されますが、$(i, j')$がデータセット$\mathcal{D}$に存在している場合はそれを除外して再生成します。上記関数の最大化は、positive sampleとnegative samplesが混ぜこぜに与えられたときに、どれがpositive sampleかを当てる確率を最大化することに相当します。

結果は最初にお見せしたとおり、Euclide空間での埋め込みとは段違いの精度を叩き出しています。

f:id:daynap1204:20170828015724p:plain

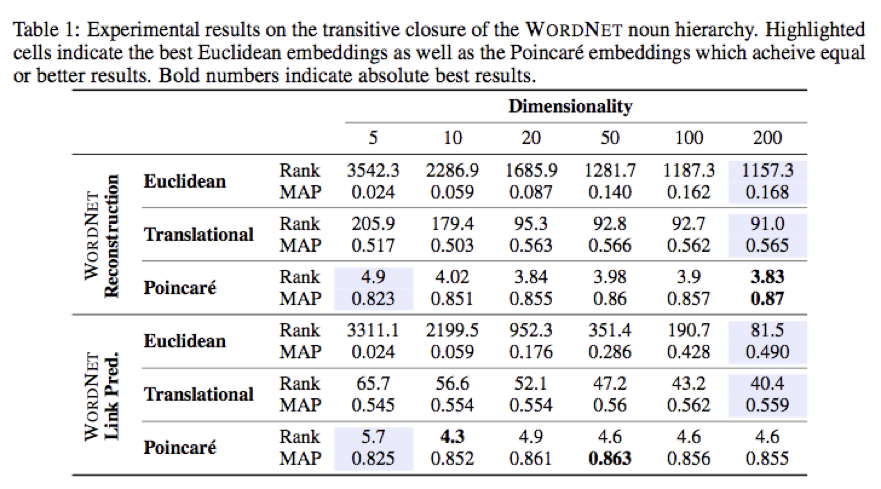
精度向上もすごいですが、個人的にとても興味深く感じるのは、その埋め込まれ方です。下記もオリジナル論文からの引用ですが、上位語ほど中心近くに配置されていることがわかると思います。正しく階層構造が抽出されていますね（もっともデータセットを作るところで作為的に（下位語、上位語）とならべているので、ちょっとズルいですが…）

f:id:daynap1204:20170828015924p:plain

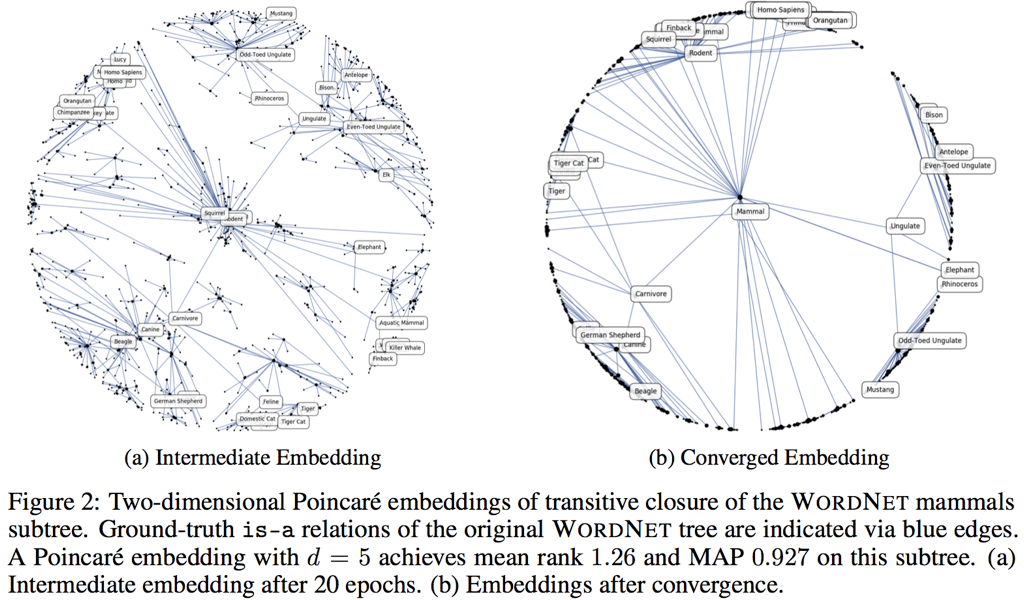
自前のコードでも同様の埋め込みを再現できたので載せておきます（私のコードを実行していただければ再現可能です）。見やすさのため、データの距離関係を保つ変換（等長変換）を施して、哺乳類（mammal）を中心に配置しています。

f:id:daynap1204:20170828020209p:plain

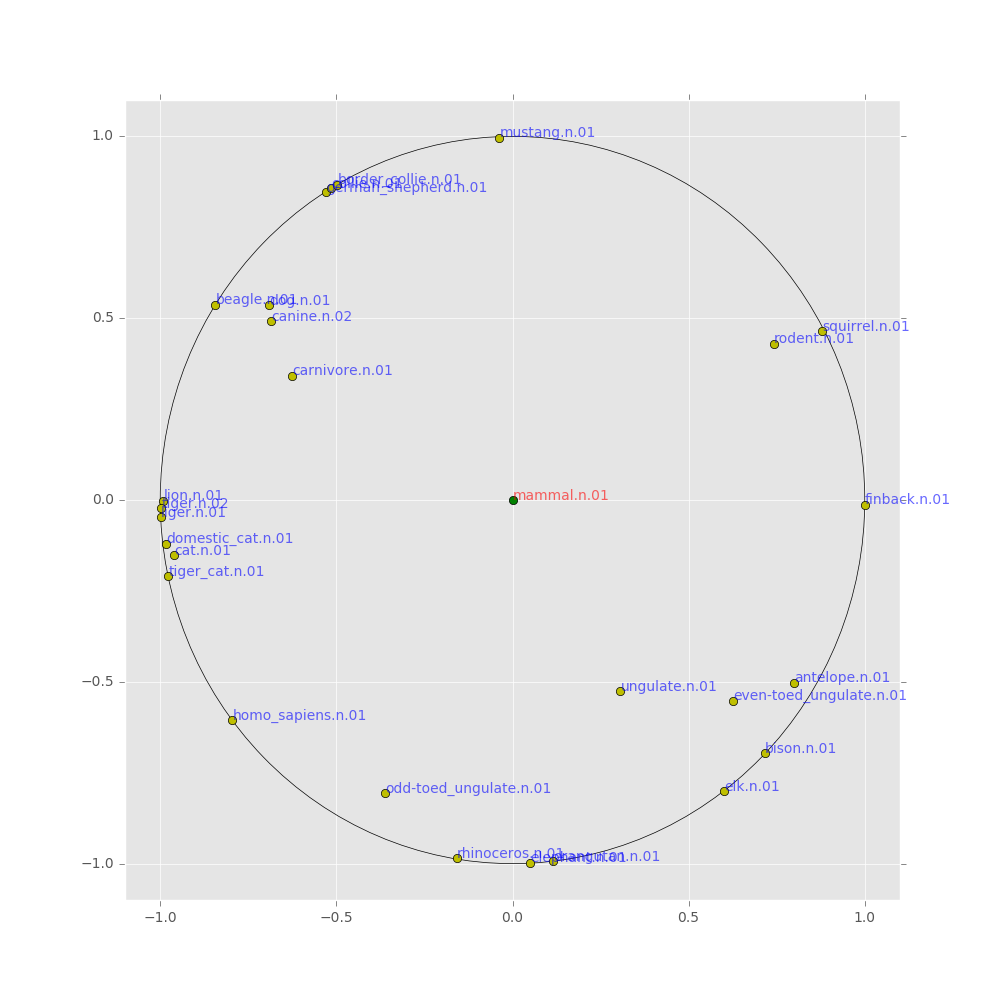
グラフのリンク予測

これは、与えられた2ノードの間にエッジが存在するかを予測するタスクです。このタスクの場合、下記の確率モデルのクロスエントロピー最大化を行います。

$$ P(e(i,j)=1; \Theta) = \frac{1}{1 + \exp((d(i,j)-r)/t)} $$

ここで、$i,j$はグラフのノードで$e(i,j)$は、それらの間にエッジが存在しているとき$e(i,j)=1$、エッジが存在していないとき$e(i,j)=0$となる関数です。$\Theta$は同様にモデルのパラメータで、$d(i,j)-r)/t$は先に説明した負値をとれるように補正済みの距離関数です。この確率モデルを最大化することにより、互いにエッジが貼られているノードほど近くに配置されるようになります。

この場合でもやはり、Euclide空間での埋め込みを上回る精度を達成しています。

f:id:daynap1204:20170828021136p:plain

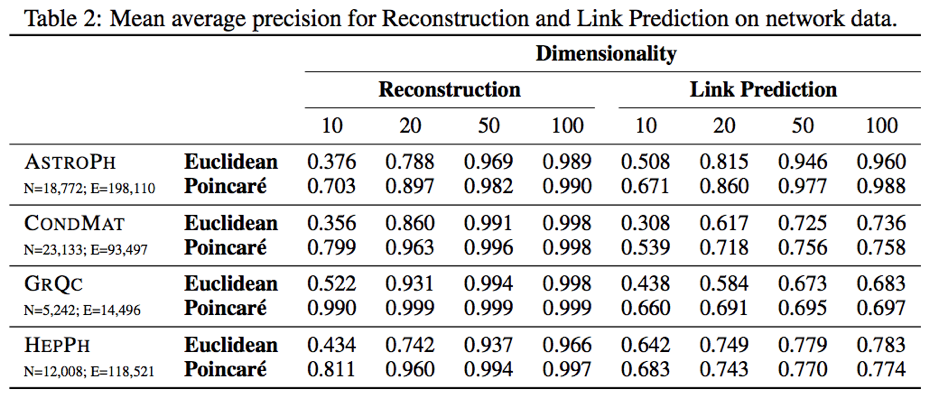
余談: Poincaré Ballにおける"内積"

内積ではなくあえて"内積”としたのは、Poincaré Ballにおける理想的な内積の定義はとても難しいと感じているからです。

Poincaré Embeddingsの論文[1]が出て間もなく、Poincaré Ballにおいて"内積"を定義し、Poincaré Embeddingsで$-d(v_i, v_i)$と表されていた類似度関数をその"内積"で置き換えた論文[11]が登場しました（この頃、何か双曲空間での埋め込みを助長するようなトリガーがあったのでしょうか？）。先日開催されたKDD2017のworkshopで発表されたようです。

www.mlgworkshop.org

この論文ではPoincaré Ballにおける"内積"を以下のように定義しています。 2点$u,v$のPoincaré Ballにおける"内積"をEuclide空間の内積$\langle u, v \rangle$と区別するために$\langle \langle u, v \rangle \rangle$と表したとき

$$ \langle\langle u,v \rangle \rangle = d(o,u) \ d(o,v) \ cos \theta .$$

がその"内積"です。ここで、$o$はPoincaré Ballの原点であり、$\theta$は2点u,vが原点oを中心に為す角の角度です。Poincaré Ballにおいて、原点ともう一点の間の測地線はその2点間を結ぶ直線になることが知られているので、$\theta$は$o$と$u$とを結ぶ測地線と$o$と$v$とを結ぶ測地線とがなす角と思うことができます。この観点から、この"内積"は、Euclide空間における内積の概念をPoincaré Ballへ拡張したものとみなすことができます。

実は私も$-d(v_i, v_j)$の代わりになる関数を探していて、同じような"内積"に思い至ったのですが、最近、以下の対応関係から、Poincaré Ballにおける"内積"の定義はPoincaré Ballの空間としての豊かさを有効活用できていないことに気づきました。

$$ \langle \langle u,v \rangle \rangle = <u', v'>, \ \ u' = \frac{d(o,u)}{\Vert u \Vert} u, \ \ v' = \frac{d(o,v)}{\Vert v \Vert} v $$

対応$u \rightarrow u',\ v \rightarrow v'$により、Poincaré BallとEuclide空間との間に1対1の対応関係ができてしまい、しかもこの対応関係は"内積"の値を保ちます。なので、せっかくPoincaré Ballで考えていたのに、Euclide空間で考えるのと同じ表現能力しか獲得できていません。

双曲空間に適切な類似度/非類似度を定義するのは今後の課題になりそうです。

おわりに

いかがだったでしょうか。Poincaré Embeddingsの可能性を少しでもお伝えできていれば幸いです。データをよりリッチな空間で表現するという方向性は従来からありましたが（kernel法もimplicitにそういうことをしていますね）、Poincaré Ballでの表現は実用上の最適解の一つかもしれません。

以前Graph Convlutionをご紹介したことがありますが[12]、Graph Convolutionがうまくいくのはグラフに局所性や再帰性、フラクタル性、階層構造があるからだと思います。これらの性質を考えるにつけ、Poincaré Embeddingsとの親和性を感じずにはいられません。双曲空間でDeep Learningが展開される将来に胸をときめかせつつ、本稿を終わりにしたいと思います。