機は熟した！グラフ構造に対するDeep Learning、Graph Convolutionのご紹介

はじめまして。ABEJAでResearcherをやらせていただいている白川です。

先日、化合物の物性推定をDeep Learningをつかって従来手法より300,000倍高速に処理するという論文がでました（[1], [2]）。この論文の手法は、Graph Convolutionというグラフ上に定義されたConvolution演算がベースとなっています。物性推定に限らず、グラフ解析全般を Deep Learning で上手にこなせるようになれば、Deep Learningのアプリケーションの幅がぐっと拡がり、さらなるイノベーションが起きそうな予感がします。 ICMLやNIPSなどの機械学習系の主要国際会議でも数年前からGraph Convolutionについての論文がちらほら出現しはじめており、とくに最近その勢いが増してきている印象があります。個人的にも最近（前から？）にわかにグラフづいていたので、この機会にグラフ上のDeep Learning、とくにGraph Convolutionについて整理して、このEmerging Technologyを盛り上げていければと思います！

グラフとして表現されるデータ

ここでいうグラフとは棒グラフとか円グラフとかのグラフではなくて、何かと何かがつながっている様を表すネットワーク構造のことを表します。 ネットワークと言うとニューラルネットワークのネットワークや通信ネットワークなどと混同しがちなので、ここではグラフ/Graphと呼ぶことにします（もっとも、ニューラルネットワーク、通信ネットワークもグラフ／ネットワークであることは間違いないですね）。 グラフはノードがエッジでむすばれることにより構成されます。エッジに向きがついているとき有向グラフといい、そうでないとき無向グラフといいます。同一ノードを結ぶエッジ（ループ）を考えたり、同じノード間に複数のエッジ（多重エッジ）が張られた状況を考える場合もあります。

グラフの典型的な例としては、ソーシャルネットワークがあります。

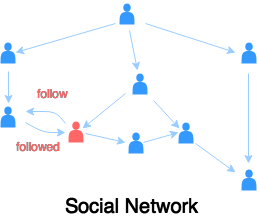
皆さんの身近にもグラフの例は無数にあります。それこそ「つながり」が存在するものすべてはグラフといえるかもしれません。 グラフやグラフ上でのアクティビティなどすぐに思いつくだけでも

• Internet
• Web
• 電力供給網
• 交通網
• 購買データ（誰が何を買ったか）
• 動画や音楽の視聴履歴
• Webアクセス履歴
• 論文の共著関係
• メールのやりとり
• サプライチェーン
• 化合物の分子構造
• タンパク質
• センサーネットワーク
• 感染症の伝播経路
• 進化系統樹
• 神経系
• 脳内の各部位の関係性ネットワーク
• 3Dオブジェクトのポリゴン表現
• プログラムのクラス図

などなど。 こちらのWebサイトでは様々なデータをグラフとして描画していて眼に楽しいです。

www.visualcomplexity.com

この他にも画像やテキストもグラフとして捉えることができます。

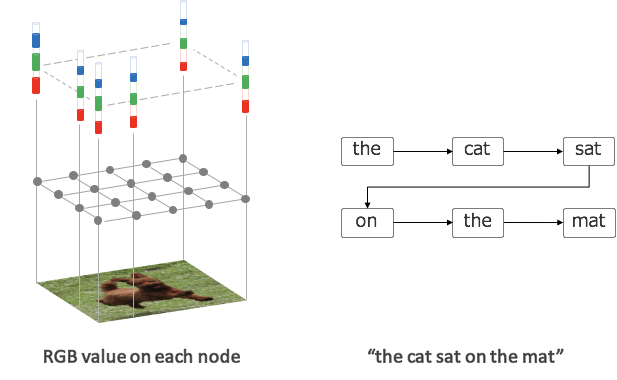
画像の場合、グラフのノード=ピクセルにはRGBの色情報が載っています。テキストの場合は単語を出現順に結んだグラフ（上の遷移）となります。 テキストについては、係り受け関係でグラフをつくってもよいかもしれません。 このように画像やテキストなどの従来からDeep Learningで取り扱われてきた対象も、その上部構造としてグラフ構造を想定することができます。

後々のため、グラフに対する要件を整理しておきましょう。

• エッジには向きがついている場合（有向）とそうでない場合（無向）がある
• ふたつのノードの間に複数種のエッジが張られている場合がある
• ループ（同一ノードを結ぶエッジ）がありえる
• ノードには属性が紐付いていることがある（画像のRGBなど）
• エッジには属性が紐付いていることがある
• エッジには重みが紐付いていることがある、等々

Graph Convolution

グラフ上でDeep Learningを展開する技術、なかでもGraph Convolutionと呼ばれる技術が最近のトレンドになってきていると感じています。 以下では、Graph Convolutionの実現方法について、いくつかの論文を引き合いに出しながらご説明したいと思います。

どこがむずかしいのか

実は最近までGraph上のDeep Learningは一部の研究者を除くと、それほど注目されていなかったように感じます。個人的にはそれは技術的な理由によるところが大きいと考えています。 というのも、最近のDeep Learningのキーとなる構成要素はConvolutionという操作なのですが、これをGraph上に適切に定義するのが一筋縄ではいかないのです （発展途上の技術のため、Deep Learningのフレームワークのサポートが十全ではないのも理由かもしれません）。

まずは画像の場合のConvolutionを考えてみます。 Convolutionは画像の各ピクセルに対してその周辺のピクセルの値を重み付けして足し合わせる操作のことを指します。 この際、「周辺のピクセル」としては3x3とか5x5といった、注目しているピクセル中心の正方形領域（フィルターと言います）を考えることが多いです。 またConvolutionの重みは、いずれのピクセルを中心に考えるときにも同じ重みを使います。たとえば下図（[3]）の場合、青色の7x7の画像上を3x3のフィルターが走査することで5x5の出力が得られますが、このフィルターの3x3の各マス目には固有の重みが紐付いていて、各出力はその重みで配下の画像のピクセル値を重み付け和することで計算されます。

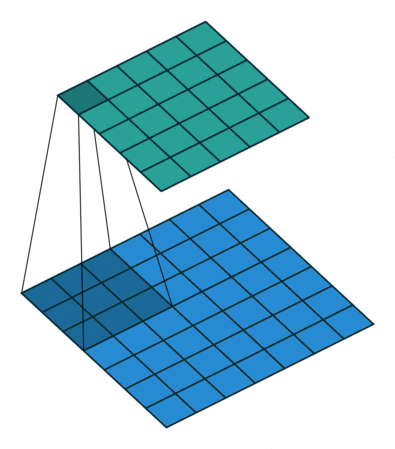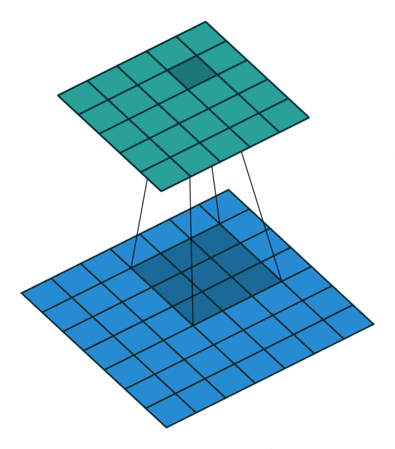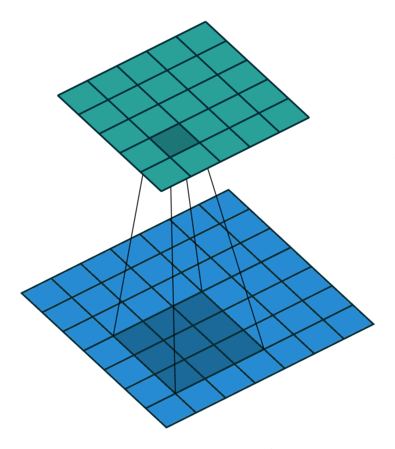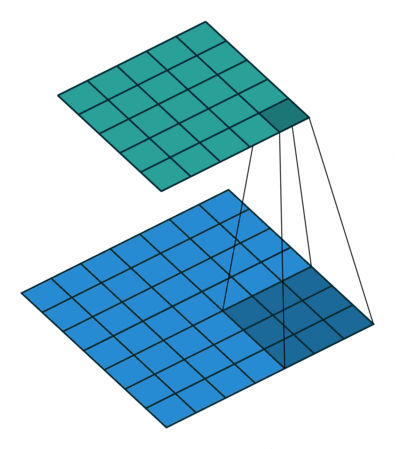
Graphについても画像と同様にConvolutionを定義したいのですが、画像の場合と異なり決定的な難点が立ち現れます。それはグラフの注目ノードの周りの周辺ノードの接続関係が注目ノードごとに不定形であるかもれしれないという点です。

この難点をヒューリスティックもしくは理論的なアプローチにより解決したのが今回ご紹介するGraph Convolutionになります。

Graph Convolution の構成

Graph Convolutionの構成方法を思い切って分類すると、下記の2タイプになります。

1. Graph Fourier変換を利用した構成
2. より直接的な構成

それぞれご説明します。

Graph Fourier 変換を利用した Graph Convolution の構成

といいつつ以下の議論は少し技術的になってしまうので、読み飛ばせるように先に結論だけまとめておきます。

• ループや多重エッジをもたない重み付き無向グラフに対しては、理論由来のわりと正統的な方法で Graph Convolution が定義できる

もうちょっと詳細（技術的）には、

1. ループや多重エッジを持たない重み付き無向グラフに対しては Graph Fourier 変換という、通常の意味での Fourier 変換のアナロジーを定義することができる
2. Graph Fourier変換に対してConvolution Theoremを適用することでGraph Convolutionを定義することができる
3. うまくパラメータ付けすることで、ノードの隣接関係を考慮したGraph Convolutionも定義できる([6])

という具合になります。Graph Fourier変換とは、グラフ上の信号（ノードに対して付与されたベクター値）に対して定義される、Fourier変換に似た操作です。 Fourier変換は波形信号を周波数成分ごとに成分分解する変換ですが、Graph Fourier変換はグラフ上で定義された信号を「ゆるやかな信号」や「急峻な信号」へ成分分解する変換となります。

もし仮にGraph Fourier変換が定義できたとすると（構成方法はあとで説明します）、ConvolutionはFourier Domainにおける要素積に相当するという定理（Convolution Theorem)

$$\displaystyle \widehat{f * g} = \widehat{f} \odot \widehat{g} \ \ \ \ ( \widehat{f}はfのFourier変換、*, \odotはそれぞれConvolution, 要素積を表す) $$

を適用することで

1. グラフ上の信号（= 各ノードに割り振られた特徴ベクター）に対してGraph Fourier変換を施す
2. 変換された信号に対して、何かと要素積をとる
3. 要素積の結果に対して逆Graph Fourier変換を施す

というようにして間接的にグラフに対してConvolutionを定義することができます。 ここで2の「何か」はFourier領域において表現されたConvolutionです。

Graph Fourier 変換

以下の議論はだいぶ技術的になります。詳細については[5]を参照してください。 ループや多重エッジをもたない、重み付き無向グラフ $ \mathcal{G}=(\mathcal{V}, \mathcal{E}, \mathcal{W}) $を考えます。$ \mathcal{V}, \mathcal{E} $はそれぞれグラフ$ \mathcal{G}$のノード、エッジの集合です。$ \mathcal{W}$は $(i,j)$ 成分 $W_{i,j} \geq 0$ がエッジ $(i,j)$ の重みを表す対称行列です。$N=|\mathcal{V}|$をグラフ$\mathcal{G}$のノード数とします。

Graph Fourier変換はグラフ $\mathcal{G}$ 上の信号に対するある種の信号変換として定義されます。ここでグラフ上の信号とは、グラフの各ノードに対する $d$ 次元ベクターの割り当てのことを指します。以下の図（[5]より引用）は、$d=1$ のケースの信号です。$d>1$ の場合、こういった1次元信号が $d$ 個あると思ってください。

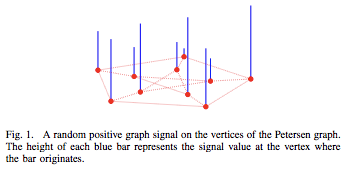
Graph Fourier変換のしたいことは、与えられた信号を「なだらかな信号」や「急峻な信号」など、信号の緩急に応じた成分へ分解することです。 $\mathbf{x} \in \mathbb{R}^{N}$ を1次元信号とするとき、信号のなだらかさや急峻さを下記で定義します。

$$ \displaystyle \sum_{i, j} {W_{i, j} ( x_i - x_j )^2} \tag{1}. $$

上式を最小化する（つまりもっともなだらかな）信号は定数信号です。そのうちから二乗ノルムが 1 のものをとって、これを $\mathbf{u}_0$ と表すことにします。 $i=0,1,2,...,N-2$に対して帰納的に

$$ \displaystyle \mathbf{u}_{i+1} = \mathop{\arg \min}\limits_{\mathbf{x} \in \mathbb{R}^{N}, | \mathbf{x} | = 1, \mathbf{x} \perp { \mathbf{u}_0, ... , \mathbf{u}_i } } \sum_{i, j} W_{i, j}(x_i - x_j) ^ 2 $$

と定めると、${ \mathbf{u}_0, ..., \mathbf{u}_{N-1} }$ は $\mathbb{R}^N$ の正規直行系になります。

なお、(1)式はGraph Laplacian $L$を用いて簡易に表現することができます。 Graph Laplacianは、Graphの次数行列(Degree Matrix)、隣接行列(Adjacency Matrix)を用いて下図（[4]）のように定義される行列です。 次数行列は、対角成分に各ノードの次数=接続エッジ数を並べたもの、隣接行列は $(i,j)$ 成分に $i$ 番目のノードと $j$ 番目のノードにエッジが張られている場合に1を、そうでない場合に0を並べた行列です。

このGraph Laplacianを用いると(1)式は $$\displaystyle \sum_{i, j} {W_{i, j} ( x_i - x_j )^2} = 2 x^T L x $$ と表現されることが知られています。さらに${ \mathbf{u}_0, ..., \mathbf{u}_{N-1} }$は$L$の固有ベクターとなることもわかります（これらは簡単な計算で確かめられます）。${ \mathbf{u}_0, ..., \mathbf{u}_{N-1} }$はたとえば下記のような具合になります([5])。

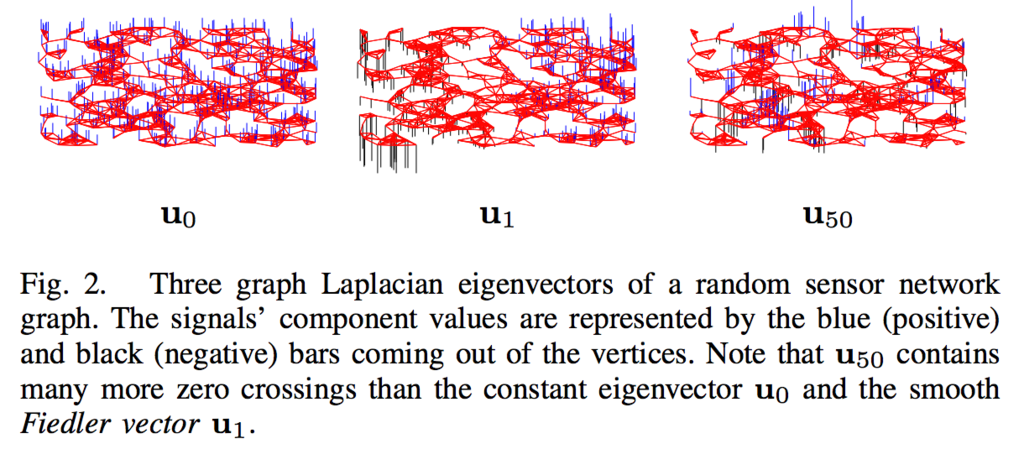
さて本題のGraph Fourier変換ですが、これは $\mathbf{x}$ の基底 ${ \mathbf{u}_0, ..., \mathbf{u}_{N-1} }$ に関する直行変換

$$ \displaystyle \mathbf{x} = \sum_k \alpha_k \mathbf{u}_k, \ \ \ \ \ $$

における係数ベクターへの対応 $\mathbf{x} \rightarrow \widehat{\mathbf{x}} = \mathbf{\alpha} = (\alpha_0, \alpha_1, ..., \alpha_{N-1})$ として定義されます（ここで $\alpha_k = \langle \mathbf{x}, \mathbf{u}_k \rangle$ は$\mathbf{x}$と$\mathbf{u}_k$の内積です）。$U=(\mathbf{u}_0, ..., \mathbf{u}_{N-1} )$ととれば、Graph Fourier変換は$\widehat{\mathbf{x}} = U^T \mathbf{x}$と簡潔に表現できます。逆Graph Fourier変換を、$\widehat{\mathbf{x}} \rightarrow \widehat{\widehat{\mathbf{x}}} = U \widehat{\mathbf{x}}$として定義します。

Graph Fourier変換、逆Graph Fourier変換が定義できたので、Graph Convolutionを定義することができます。Convolution TheoremによるとConvolutionはFourier変換後には要素積として表現されるので、 乗じる係数ベクターを$\mathbf{\theta}=(\theta_0, ..., \theta_{N-1})$とすると、Graph Convolutionは

1. グラフ上の信号（=各ノードの特徴ベクター）に対してGraph Fourier変換を施す: $\mathbf{x} \rightarrow \widehat{\mathbf{x}} = U^T \mathbf{x}$
2. 変換された信号に対して、$\mathbf{\theta}$と要素積をとる: $\widehat{\mathbf{x}} \rightarrow \mathbf{\theta} \odot \widehat{\mathbf{x}}$
3. 要素積の結果に対して逆Graph Fourier変換を施す: $ \mathbf{\theta} \odot \widehat{\mathbf{x}} \rightarrow U (\mathbf{\theta} \odot \widehat{\mathbf{x})}$

となります。合わせるとGraph Fourier変換により定義されるGraph Convolutionは $$ \displaystyle \mathbf{x} \rightarrow U (\mathbf{\theta} \odot (U^T {\mathbf{x}))} \tag{2} $$ という対応になります。いまは1次元信号を考えましたが、$d$次元信号($d \ge 1$)を考える場合は、各次元ごとにconvolutionをした結果を総和します。

なお、上記は比較的一般的な構成でしたが、$L$の$(\mathbf{u}_0, \mathbf{u}_1, ..., \mathbf{u}_{N-1})$に対応する固有値を$\mathbf{\lambda} = (\lambda_0, \lambda_1, ..., \lambda_{N-1})$として、それらを対角にならべた行列を$\Lambda = diag(\lambda_0, \lambda_1, ..., \lambda_{N-1})$とすると、実対称行列の固有分解により$L=U \Lambda U^T$ですので、$\mathbf{\theta}=\mathbf{\lambda}$ととったとき(2)式は $$ \displaystyle \mathbf{x} \rightarrow U (\mathbf{\theta} \odot (U^T {\mathbf{x}))} = U \Lambda U^T \mathbf{x} = L\mathbf{x} $$ と簡単に表されます。この特殊な場合のGraph Convolutionは各ノードごとにそのノードの隣接ノードのみに依存します。同様に$L^2 \mathbf{x}, L^3 \mathbf{x}, ...$は各ノードから2エッジ、3エッジ、…離れたノードにのみ依存します（局所性）。論文[6]では$L$のかわりに$L$の$K$次多項式 $g(L) = \sum_{k = 0}^K \alpha_k L^k$ ($\alpha_k$ はパラメータ)を作用させることで局所性を考慮したGraph Convolutionを提案しています。 また、論文[7]では$g(L)$の次数を一次($K=1$)までに限定したGraph Convolutionをノードの半教師あり分類問題に適用する手法を提案しています。 これらの手法については、下記の記事も参考になります。

www.inference.vc

より直接的なGraph Convolutionの構成

Graph Fourier変換由来の定義の場合、技術的な理由から、ループや多重エッジをもたない、重み付き無向グラフに限定する必要があります。 ですが、そもそもGraph Fourier変換を介してGraph Convolutionを定義する必然性はあるのでしょうか？ グラフの接続関係は既知なので、これだけを使って定義する事はできないのでしょうか？（そもそもGraph Laplacian自体、接続関係のみから定義されるような代物でした）

そのような観点にたつと、より直接的なGraph Convolutionの定義をしたくなります。例によってこちらも技術的になるので先に結論を述べておきます。

• ノードやエッジの接続関係のみから、より直接的にGraph Convolutionを定義することができる（理論由来ではない）
• こうして定義されたGraph Convolutionには有向グラフや多重エッジ、ループなどのより複雑な構造も自然に導入できる

なお、冒頭に上げたGoogleによる化合物の物性推定へGraph Convolutionを適用した際のGraph Convolutionはこちらの直接的な定義にもとづいています。 ほかにもKnowledge Baseの解析にも適応されたりしています[8]。

どう定義するか

考え方の基本は簡単です。多種データの取り扱いに困ったときは、ひとまず線形和にしてNeural Networkに入力。これだけです。非常にDeep Learning的な考え方です。

具体的なケースで考えやすいように、[8]にしたがってKnowledge Baseを例にとって考えてみます。ここではKnowledge Baseを「AはBである(A, is-a, B)」とか「AはBを持っている(A, has-a, B)]のような3つ組が羅列された集合とします。このときKnowledge Baseは下図([8]より引用)のように、A, Bをノードとしてis-aやhas-aなどの関係性をAからBへの有向エッジとする多重有向グラフとして表現されます

このグラフの場合、下記を考慮する必要があります。

• エッジは有向
• ノードに属性がある

目標は、各ノード$v$にそのノードの何らかの属性を表す信号$\mathbf{x}_v \in \mathbb{R}^d$が乗っているものとして、他のノードとの接続関係をもとに Graph Convolution を定義して、それを適用することで信号を更新していくことです。最終的にそうして更新されていった信号からノードの属性予測や未知の関係性の予測を行います。先にあげたKnowledge Baseの図で言えば、赤いノード、エッジが予測により補完されるべきノードの属性、関係性になります。

[8]ではこれらを下記のように構築します。

この図の意味するところを説明します。まず、各ノード$v$ごとにその隣接ノードを接続のされ方に応じて分類します。具体的には、

• ノード$v$に入力されたエッジか出力されたエッジか
• そのエッジの表す関係性は何か

の2種の情報の組み合わせとして接続のされ方を区別します。これらの接続のされ方ごとにノード$v$の近傍が変わるものと考えます。 ついで、それぞれの接続のされ方に応じた近傍ごとに、近傍ノードの信号の総和（もしくは平均）をとった後、接続のされ方に応じた線形変換を施し足しこんでいきます。これにより、エッジの向きやエッジの関係性を加味した足し込みがなされますが、この足し込まれた表現をこのケースでのGraph Convolution操作として定義します。[8]で提示されている式を示しておきます（ノード $i$ の信号の更新式になっています。Graph Convolution後に非線形変換$\sigma$を施しています）。

$$ \displaystyle h^{(l+1)}_i = \sigma \left( \sum_{r \in \mathcal{R}} \sum_{j \in \mathcal{N}^r_i} \frac{1}{c_{i, r}} W^{(l)}_r h^{(l)}_j + W^{(l)}_0 h^{(l)}_i \right). $$

コンセプトが非常にわかりやすい論文なので、[8]はオススメです。考え方が素直なので、グラフがより複雑になっても素直に拡張できそうですね。

冒頭でご紹介したGoogleの化合物物性予測の論文([1],[2])は、既存のGraph Convolutionの実現法を

1. message (近傍からどんな情報を取得するか)
2. update (messageからどのように信号を更新するか)
3. readout (グラフの信号から「グラフ自体」の特徴をどう読み取るか）

に機能整理した上でフレームワーク化しています（MPNN, Message Passing Neural Networks framework）。 既存研究の整理としては非常にわかりやすい論文です。 具体的なモデルや実装の詳細があまり明らかになっていないのですが、物性予測のための手法としては、今後、こういったGraph Convolution由来の 手法がベンチマークとなっていくのではないでしょうか。

おわりに

お付き合い頂きありがとうございます。 Graph Convolutionはまだまだ発展途上の技術ですが、最近になってようやく機が熟してきた感があります。 静的なグラフの解析だけでなく、RNN/LSTMと組み合わせることで動的なグラフの解析を可能にする手法([9],[10])や、テキストの係り受け関係を捉えるのにGraph Convolutionを適用した論文([11])など、Graph Convolutionはすでに要素技術として確立してきています。 本記事執筆中に開催されている、Deep Learning周辺の先端的な話題を取り扱う国際的なworkshop会議ICLR2017にも、Graph Convolution関連の論文が数本採択されていたりと、これから間違いなく来る技術と信じていますので、これからも継続的に研究していきたいと思います。

宣伝

ABEJAでは最先端技術にピピっとくる、イケててヤバいエンジニアを募集しています。 一緒にGraph Convolutionを盛り上げていきたい方、その他Emerging Technologyを開拓していきたい方等々、是非お待ちしております！

ABEJAが発信する最新テクノロジーに興味がある方は、是非ともブログの読者に！

ABEJAという会社に興味が湧いてきた方はWantedlyで会社、事業、人の情報を発信しているので、是非ともフォローを！！ www.wantedly.com

ABEJAの中の人と話ししたい！オフィス見学してみたいも随時受け付けておりますので、気軽にポチッとどうぞ↓↓

参考文献

[1] J. Gilmer et al., "Neural Message Passing for Quantum Chemistry", arXiv preprint arXiv:1704.01212, 2017

[2] https://research.googleblog.com/2017/04/predicting-properties-of-molecules-with.html

[3] https://github.com/vdumoulin/conv_arithmetic

[4] https://en.wikipedia.org/wiki/Laplacian_matrix

[5] D. I. Shuman et al., "The Emerging Field of Signal Processing on Graphs: Extending High-Dimensional Data Analysis to Networks and Other Irregular Domains", IEEE Signal Processing Magazine, 30(3):83–98, 2013

[6] B. Defferrard et al., "Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering", NIPS2016

[7] T. N. Kipf et al., "Semi-Supervised Classification with Graph Convolutional Networks", ICLR2017

[8] M. Schlichtkrull et al., "Modeling Relational Data with Graph Convolutional Networks", arXiv preprint arXiv:1703.06103, 2017

[9] Y. Seo et al., "Structured Sequence Modeling with Graph Convolutional Recurrent Networks", ICLR2017

[10] F. Manessi et al., "Dynamic Graph Convolutional Networks", arXiv preprint arXiv:1704.06199, 2017

[11] D. Marcheggiani et al., "Encoding Sentences with Graph Convolutional Networks for Semantic Role Labeling", arXiv preprint arXiv:1703.04826, 2017