双曲空間でのMachine Learningの最近の進展

ABEJAでReseacherをしている白川です。

以前、Poincaré Embeddingsという双曲空間への埋め込み手法をご紹介しました。当時、木構造データを5次元の空間に精度良く埋め込めるということで話題になったのですが、その後双曲空間での機械学習手法が多数研究・提案され、双曲空間での機械学習についての理解をバージョンアップする必要があるなと感じたので、最近の研究の進展を中心に理論背景含めてご紹介したいと思います。

tech-blog.abeja.asia

Tl;dr

本記事で伝えたいのは、論文の各論というより、各種論文で共通/独自に主張されている下記のような内容です。

• 木なら2次元で十分
• 双曲空間では指数写像/対数写像が明示的に計算され空間全体に拡張されるので取扱が容易
• Gyrovector space: 双曲空間における線形代数のような代数構造
• Riemann幾何とGyrovector spaceの整合
• 双曲空間とガウス分布のFisher情報幾何の対応

Poincaré Embeddingsのおさらい

(https://github.com/facebookresearch/poincare-embeddings から引用)

以下は以前のブログ記事の一節です。

Poincaré Embeddingsは大雑把に言えばword2vecを異空間で実現する技術で、双曲空間（Hyperbolic Space）という、おなじみのEuclide空間（2点$x,y$の間の距離を$\sqrt{(x_1 - y_1)^2 + (x_2 - y_2)^2 + ... + (x_d - y_d)^2}$で測るいつもの空間）とは異なる空間でデータを表現します。それにより、従来手法（word2vecのようにEuclide空間へ埋め込む手法）では200次元くらいのベクトル表現を要していたケースで、なんと5次元で遥かに高い精度を達成することに成功しています。

100次元とか200次元とかの埋め込みがふつうであったところを、双曲空間への埋め込みを行うことでたった5次元で高精度に埋め込んだというのが当時は衝撃的でした。

双曲空間はユークリッド空間とは異なり、曲がった空間（多様体）です。数学的には（断面）曲率という空間の曲がり具合を測る尺度があって、これがいたるところ定数の（連結な）空間は下記の3種類に分類されることが知られています。

• 曲率 = 0 → ユークリッド空間
• 曲率 > 0 → 超球面
• 曲率 < 0 → 双曲空間

ユークリッド空間はのっぺりと広がった空間ですが、超球面はいたるところ収縮してくるんと丸まった空間です。一方で双曲空間はいたるところ外へ向かって拡散しており、これにより双曲空間はユークリッド空間に比べても圧倒的に広い空間になります。たとえば$n$次元ユークリッド空間では球の体積は半径$r$にたいして $r^n$ に比例するかたちで増えていきますが、双曲空間の場合には球の体積は $\exp(r)$ に比例しますので、その空間の広がり方は圧倒的です。

簡単な木構造である二分木（各ノードが２つの子をもつ木）でさえも、ルートノードの$d$個下の子ノードの総数は $2^d=\exp(d \log2)$ 個になるので、指数関数的にノードが増えていきます。この子ノード、孫ノード、…の個数の増え方のせいで、ユークリッド空間は木構造を埋め込むには狭すぎる空間となります。

Poincaré Embeddingsの詳細についてご興味ある方は冒頭にあげた以前の記事をご参照ください。

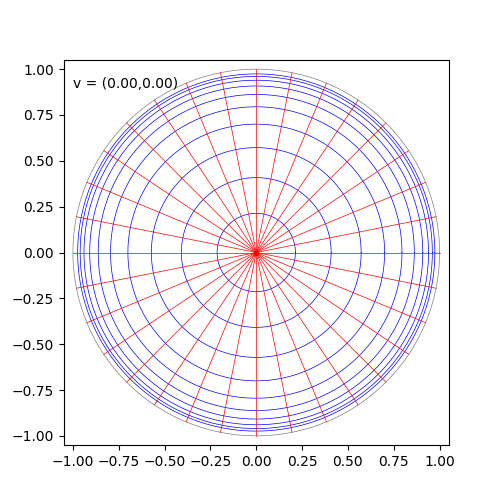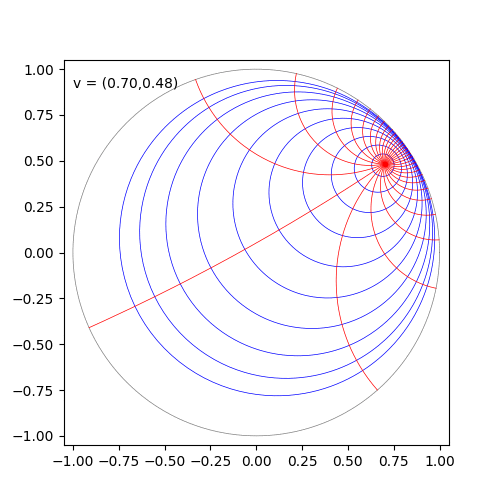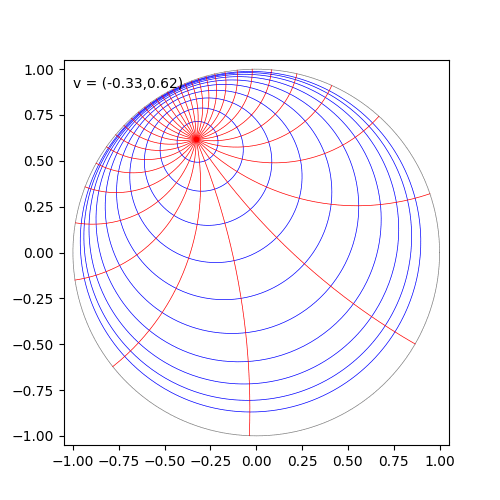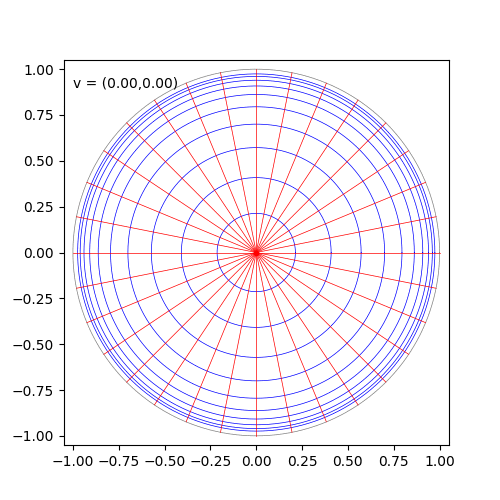
Poincaré disk/ball モデル（モデルというのは双曲空間の異なる座標表示方法のことです）については、下記の記事で公開されている可視化が理解に役立ちます。 nunuki.hatenablog.com

hyperbolic maze

このgifアニメーションはPoincaré diskの境界方向へ進んでも空間が爆発的に拡がっていることを示しています。双曲空間の場合、このアニメーションのように無限分岐するツリーが表現可能ですが、ユークリッド空間では分岐を重ねていくとそのうちどん詰まりになってしまうはずです。

geodesics

このアニメーションは双曲空間における2点間の最短曲線（測地線、geodesic）を表しています。空間がゆがんでいるため、最短曲線はユークリッド空間のような直線にはならず、円盤の縁に直交的に交わる円弧か中心を通る直線（半径無限大の円弧）になります。

双曲空間での機械学習の最近の進展

ここ1-2年の双曲空間での機械学習の進展は目をみはるものがあります。下記は最近の双曲空間での主な機械学習手法をまとめたものです（応用系の研究は省いています）。発表年はarXivへの投稿日を基準にしています。

Machine Learning Methods in Hyperbolic Space

発表年	論文名	著者	内容
2017/5	Poincaré Embeddings for Learning Hierarchical Representations	M. Nickel+	Poincaré ballへの埋め込み(Poincaré Embeddings)を提案し、木構造データを低次元で精度良く埋め込めることを示した。
2018/1	Learning Continuous Hierarchies in the Lorentz Model of Hyperbolic Geometry	M. Nickel+	Poincaré ballではなくLorentz model (Hyperboloid model)という別の双曲空間のモデルで埋め込みを構成し、Poincaré Embeddingsより安定的に最適化可能なことを示した 。
2018/4	Representation Tradeoffs for Hyperbolic Embeddings	C. D. Sa+	Sarkar's Constructionという木構造をPoincaré disk（2次元双曲空間）へ任意精度で埋め込む既存手法をn次元のPoincaré Ballへ拡張し、木構造データに対し2次元でPoincaré Embeddingsを超えるほぼ完全な精度の埋め込みを実現。双曲空間に埋め込む際、Ballの周辺を表現し分けるには浮動小数点の精度を大きくとる必要があることも示した。さらにユークリッド空間でのPCAをリーマン多様体に拡張したPGA（Principal Geodesic Analysis）を適用することで、点の間の距離情報のみから完全な埋め込みを復元するh-MDS（Hyperbolic Multidimensional Scaling）を提案。
2018/4	Hyperbolic Entailment Cones for Learning Hierarchical Embeddings	O-E. Ganea+	Poincaré Ballに点として埋め込むのではなく、Coneとして埋め込むことで埋め込み間の包含関係のより明確な表現を実現。
2018/5	Hyperbolic Neural Networks	O-E. Ganea+	双曲空間のRiemann幾何学とMöbius gyrovector spaceの関係性を示すことで、双曲空間でのNeural Networksの構成の一例を示した。
2018/5	Hyperbolic Attention Networks	C. Gulcehre+	gyrovector spaceにおける中点の概念を延長することで、双曲空間におけるattentionの構成方法の一例を示した。また、Hyperboloid modelの点のパラメータ付を与えることで、ユークリッド空間での表現と双曲空間での表現の間の移行方法の一例を示した。
2018/10	Poincaré Glove: Hyperbolic Word Embeddings	A. Tifrea+	Gloveを双曲空間で再構成した。ガウス分布間のフィッシャー情報距離とガウス分布の平均、分散の間の双曲空間（上半平面モデル）での距離との対応関係（既存研究）を考えることで、双曲空間での埋込における意味的な親子関係/包含関係の解釈を与えた。

Poincaré Embeddingsが出た当時と比べて、Riemann幾何やgyrovector space（ユークリッド空間におけるvector spaceの理論の対応物）のような双曲空間の幾何学的・代数的特性をフルに使った研究が続々と出てきています。Poincaré Embeddings 以外の手法について下記で概観します（図は各論文から引用しています）。

…が、非常に長くなってしまうので、気になる論文があればつまみぐいしていただいて結論へ飛んでいただくのがいいかもしれません。

Learning Continuous Hierarchies in the Lorentz Model of Hyperbolic Geometry

Poincaré Embeddings ではPoincaré disk/ball modelという双曲空間のモデルを採用していましたが、この論文ではLorentz model (hyperboloid model)という別の双曲空間のモデルを採用しています。

双曲空間のモデルというのは，双曲空間の異なる座標表示の仕方に対応しています（曲がった空間なので、座標表示の仕方に工夫が必要です）。よく知られたモデルとしては例えば下記のようなものがあります（各モデルの図はリンク先のwikipediaのページから引用しています）。それぞれのモデルは一瞬違って見えますが、お互いに距離を保つような写像（等長写像）によって移り合うので、その意味で等価なモデルですが、本来曲がっている空間の点を無理に座標表示するため、それぞれ表現方法には一長一短があります。詳細は英語版のwikipediaなどを参照してください。

en.wikipedia.org

Poincaré disk/ball model

半径1の球（2次元なら円盤）のとして表現されます。測地線（二点間の最短線）は中心を通る直線か球の境界と直行して交わる円弧になります。また、ユークリッド空間と共形（conformal, リーマン計量がユークリッド空間の計量の関数倍）なので、Poincaré disk/ball modelで測った角度はユークリッドで測った角度と一致します（一般にはこうなりません）。球内に表現され、測地線も簡単なので可視化に優れています。

geodesics

上半平面モデル

n次元ユークリッド空間の上半空間として表現されます。測地線は上半平面の境界に直行する円弧か鉛直線（半径無限の円弧に対応）になります。Poincaré disk/ball modelと同様、ユークリッド空間と共形なので、上半平面モデルで測ったときの角度はユークリッド空間で測ったときの角度に一致します。

Beltrami-Klein model

Poincaré disk/ball modelと同様半径1の球内にデータが表現されますが、Poincaré disk/ball modelとは異なり、測地線は直線になります。

Beltrami-Klein model

Lorentz model / Hyperboloid model

双曲空間の親玉のようなモデルで他の各種のモデルはこのモデルを適当に射影して得られたりします。また、実装上は一番扱いやすいモデルかもしれません。というのも、二点間の距離が$d(\mathbf{x}, \mathbf{y}) = \cosh^{-1}(x_0 y_0 - x_1 y_1 - ... - x_n y_n)$という比較的簡単な形で書けるからです。

Red circular arc is geodesic in Poincaré disk model; it projects to the brown geodesic on the green hyperboloid.

---

Lorentz modelでの埋め込みに戻ります。この論文では、Lorentz modelへの埋め込みをすることで、Poincaré Ballへ埋め込むPoincaré Embeddingsに比べてより容易に精度良く埋め込めたと報告されています。個人的にはPoincaré Embeddingでの最適化の場合、空間の計量を近似的にしか考慮していなかったので（正確なRiemannian SGDではなかった）、Lorentz modelでより正確なRiemannian SGDを行ったことなどが精度向上につながったのではと思います。

Representation Tradeoffs for Hyperbolic Embeddings

個人的には一押しの論文です。この論文では

• Sarkar's Constructionという木をPoincaré disk（2次元の双曲空間）へ任意精度で距離を保って埋め込む既存方法をn次元へ拡張
• その埋め込み方法とそれを実行するのに必要な浮動小数点精度の評価を行った
• 任意の2点の間の距離だけ与えられた場合に双曲空間への最適な埋め込みを求める手法（h-MDS）を提案

という盛りだくさんな内容ですが、いずれも理論背景がカッチリしていて、その割に読みやすいのでおすすめです。

本論文で紹介されているSarkar's Constructionは下記の論文で提案された木をPoincaré diskへ組み合わせ的に埋め込む方法です。

• R. Sarkar. "Low distortion Delaunay embedding of trees in hyperbolic plane", GD2011

Sarkar's Construction

やり方は単純で、注目しているノードの子を、

1. 注目しているノードがPoincaré diskの中心にくるように変換（メビウス変換）
2. 変換後の親ノードと同じ半径の円周上に子を親+子が等角度に並ぶように配置
3. 1の変換でもとにもどす

を繰り返すだけです。1の変換は、冒頭にあげた下記アニメーションでいうと、分岐点まで進むことに相当します。

hyperbolic maze

この構成を2の円周の半径rを大きく取ることで任意精度で木の距離（1親等、2親等など）をたもったまま埋め込むことができることが示せます。 本論文では、このSarkar's Constructionをn次元の双曲空間に拡張するのですが、アイデアは全く一緒で、

変換後の親ノードと同じ半径の円周上に子を親+子が等角度に並ぶように配置

というのを

変換後の親ノードと同じ半径の球面上に子を親+子が等間隔になるべく間をあけてに並ぶように配置

に変えるだけです。この配置自体、spherical codingという最適に解くのは難しい問題なので、超球面ではなく超立方体へ配置してから超球面に射影することで近似的に解決するそうです。

そもそも2次元（Poincaré Disk）でも任意精度で木を埋め込めてしまうので$n$次元にする必要性がどこにあるかという疑問が生じますが、本論文によると、必要な精度$\epsilon$を担保するためには$O(\frac{1}{\epsilon}\frac{l}{n} \log \deg_{max})$ ($l$は木に含まれるノード間の最長距離、$\deg_{max}$は木のノードの最大次数)以上の浮動小数点精度が必要になるので、次元を上げたほうが必要な浮動小数点精度を下げれるという利点があります。

上記だけでも興味深いですが、本論文では、h-MDS（hyperbolic multidimentional scaling）というユークリッド空間におけるMDSの拡張を提案しています。h-MDSはMDSと同様、点の間の距離データ（距離マトリックス）のみがあたえられた状況で最適な埋込を求める手法です。MDSの場合、これは主成分分析（PCA）で解かれるのですが、h-MDSの場合、PCAに相当するPGA（Principal Geodesic Analysis）を用いて解くことが出来ます。PCAではデータの分散がもっともひろがって見えるような直交軸を求めていきますが、h-MDSは、データの分散がもっともひろがって見えるような互いに直行する測地線を求めていきます。

双曲空間の場合、これは指数写像/対数写像（exponential map / logarithm map）という空間における測地線と接空間の直線を対応させるマッピングを考えることにより実現されます。

実際、双曲空間においては、指数写像/対数写像は双曲空間/接空間の全域に延長できるので、

1. 対数写像により接空間へ移行
2. 接空間でPCAを行う
3. 指数写像により双曲空間に戻す

という操作を行う事ができますが、これが双曲空間におけるPGAになります（なお、指数写像/対数写像は双曲空間の場合、closed formで計算できます！）。 本論文では、HyperboloidモデルでPGAを行い、（おそらく可視化のため）等長写像によってPoincaré ballへ写像しています。

これらの手法の結果は印象的で、下記のようにPoincaré Embeddingsよりも遥かに正確に木を埋め込めていることがわかります（FB=Poincaré Embeddings、Combinatorial=Sarkar's construction）。

Hyperbolic Entailment Cones for Learning Hierarchical Embeddings

本論文では、双曲空間への点として埋め込む代わりにcone（錐）として埋め込む方法を提唱しています。

coneとして埋め込むことのメリットは、

1. coneの包含関係 $\longleftrightarrow$ 親子関係
2. coneの重なり $\longleftrightarrow$ 共通因子の存在

という理解ができることです。これにより木ではなくDAG（Directed Acyclic Graph, 有向で巡回のないグラフ）のような子ノードでの合流を許すような構造の埋め込みも可能になります。

既存研究として、Order Embeddingsという手法があり、これはユークリッド空間において

$x = (x_1, x_2, \cdots, x_n) \leftrightarrow \{y \in \mathbb{R}^n | x_i \leq y_i, \forall i = 1, 2, \cdots n \}$

という半空間（これもcone）を考えることで、論理的な包含関係などを表現するというものです。本研究ではこれを

1. 双曲空間で錐を構成
2. 錐が満たすべき性質から錐の角度導出

と延長したものになります。詳細は論文に譲りますが、錐が満たすべき性質というのは

1. 軸に対する対称性
2. 軸に対する回転対称性
3. 距離にたいして錐の角度が連続的に変化
4. 推移則（coneの1点を先端としたconeは前者のconeに包含される）

のことです。最適化はOrder Embeddingsと同様におこわなれます（ただしRiemannian SGDです）。

下記は本提案手法の結果ですが、Poincaré EmbeddingsやOrder Embeddingsよりも高精度な埋め込みが達成されています。ただし、事前学習をPoincaré Embeddingsでガッツリ行っていたりして議論の余地はあるかもしれません…。

Hyperbolic Neural Networks

ここまでの論文は、双曲空間への点/錐としての埋め込みを扱っていましたが、本論文では双曲空間上でのNeural Networksの構成を試みています。 これができれば、双曲空間を出口として使うだけでなく双曲空間を起点として解析/学習ができるようになるので、応用が格段に広がります。

さて、その構成方法ですが、Möbius gyrovector spaceという、ちょっと聞き慣れない代数構造を用います。本気で解説しだすと本1冊とかになってしまう話題なので、詳細が気になる方は例えば下記の書籍などを参照してください（私はこの書籍で知識を仕入れました）。公理からはじめる代数的/抽象的な理論構成がちょっととっつきづらいかもしれないですが、線形代数と同じノリで読むことはできると思います。

A Gyrovector Space Approach to Hyperbolic Geometry (Synthesis Lectures on Mathematics and Statistics)

Wikipediaの記事もありますが、いきなり読むと面食らうかもしれません。

ja.wikipedia.org

あるいは相対論的なモチベーションのほうがしっくり来る方にはこの論文なども読みやすいと思います（特殊相対論では光速度を超えられないので速度の安直な足し算はNGですが、この背景には双曲空間があり、その足し算の代数構造がgyrovectorになっているそうです）。

arxiv.org

Gyrovector spaceはAbraham A. Ungarという方が中心に構築された理論で、Ungarさんを中心に調べていくと文献に当たれると思います。 本記事では、公理から始めず比較的理解しやすいPoincaré ball modelにおけるgyrovector space（Möbius gyrovector space）について、 必要そうなところだけ概念的に解説してみようと思います。

Möbius gyrovector space

Poincaré disk model（2次元）において、等長変換（isometry, 距離をたもつ変換）は鏡映変換とMöbius変換の合成で表せることが知られています。 Möbius変換というのは、Poincaré diskを複素数空間における半径1の円板$\{z \in \mathbb{C} | \vert z \vert < 1\}$と見立てた場合に下記のように定義されるマッピングです。

$$f_{a, b, c, d}: z \mapsto \frac{az + b}{cz + d},\ \ (a, b, c, d \in \mathbb{C}, ad-bc \neq 0)$$

これと行列

$$ \left( \begin{array}{ll} a & b \\ c & d \end{array} \right) \in GL(2, \mathbb{C}) $$

とは、関数の合成が行列積に対応するという事実から代数構造としては同一視出来ます:

$$ f_{a,b,c,d} \circ f_{p, q, r, s} \longleftrightarrow \left( \begin{array}{ll} a & b \\ c & d \end{array} \right) \left( \begin{array}{ll} p & q \\ r & s \end{array} \right) $$

複素単位円板を複素単位円板に1:1にマッピングするMöbius変換は、下記の形（極分解）で表せることが知られています。

$$ f_{\theta, w} : z \mapsto e^{i\theta} \phi_w(z),\ \ \phi_w(z) = \frac{z + w}{\bar{w}z + 1}, (\vert w \vert < 1) $$

この表示において、回転（$e^{i\theta}$）を無視した単位円板を単位円板に移すMöbius変換$\phi_w(z) \ (\vert w \vert < 1)$のパラメータ自身も単位円板中の点でパラメータ付けされますが、$\phi_w(0) = w$なのでそのパラメータは原点が移動した点に一致します。

ところでユークリッド空間における基本的な等長変換は平行移動ですが、これも原点がどの点に映るかで完全に特定され、変換はvectorの和$z \mapsto w + z$で記述されます。

この事実に基づき、以下のようなアナロジーを考えます。

ユークリッド空間	Poincaré Disk
平行移動	変換$\phi_w(z) \ (\vert w \vert < 1)$
vectorの足し算$w + z$	gyrovectorの足し算$w\oplus z$

すなわち、

$$ w \oplus z := \phi_w(z) = \phi_w \circ \phi_z(0) $$

と定義します。演算$\oplus$はMöbius変換$\phi_w(z)$の適用で、これの逆変換は$\phi_{-w}(z)$で与えられるので、$(-w) \oplus w \oplus z = z$などのvector演算と同様な計算などが成り立ちます。$\oplus$は関数適用で定義されているので、一般に非可換（$w \oplus z \neq z \oplus w$）な演算です。

ちょっと計算すると

$$ w \oplus z = \phi_w(z) = \frac{z + w}{\bar{w}z + 1} = ... = \frac{ (1 + 2\mathbf{w} \cdot \mathbf{z} + \Vert \mathbf{z} \Vert^2) \mathbf{w} + (1 - \Vert \mathbf{w}^2) \mathbf{z} }{ 1 + 2 \mathbf{w} \cdot \mathbf{z} + \Vert \mathbf{w} \Vert^2 \Vert \mathbf{z} \Vert^2} $$

と変形できるので（複素数$z=x + iy$と2次元vector $(x, y)$を同一視しました）、この最右辺の式でもって、n次元のMöbius gyrobector spaceにおける和を定義することが出来ます。

$$ \mathbf{w} \oplus \mathbf{z} := \frac{ (1 + 2\mathbf{w} \cdot \mathbf{z} + \Vert \mathbf{z} \Vert^2) \mathbf{w} + (1 - \Vert \mathbf{w}\Vert^2) \mathbf{z} }{ 1 + 2 \mathbf{w} \cdot \mathbf{z} + \Vert \mathbf{w} \Vert^2 \Vert \mathbf{z} \Vert^2}, \ \ (\mathbf{w}, \mathbf{z} \in \mathbb{H}^n) $$

さらに$(\ominus \mathbf{a} = \mathbf{0}\oplus (-\mathbf{a}) = -\mathbf{a})$によりマイナス倍を定義します。

ここで$\mathbb{H}^n$はn次元Poincaré ballです。

vector space においてはもう一つ演算があってそれはスカラー倍$\mathbf{x} \rightarrow r\mathbf{x} \ (r\in\mathbb{R})$ですが、gyrovector spaceにも同様にスカラー倍を定義することが出来ます。具体的には、スカラー倍の前に自然数倍$n \otimes \mathbf{x} := \mathbf{x} \oplus \mathbf{x} \oplus \cdots \oplus \mathbf{x} \ (n \in \mathbb{N})$を考えてみると、これは実は下記のように計算できることがわかります。

$$ n \otimes \mathbf{x} = \frac{ (1 + \Vert \mathbf{x} \Vert)^n - (1 - \Vert \mathbf{x} \Vert)^n }{ (1 + \Vert \mathbf{x} \Vert)^n + (1 - \Vert \mathbf{x} \Vert)^n } \frac{\mathbf{x}}{\Vert \mathbf{x} \Vert} $$

この式で$n \in \mathbb{N}$を形式的に$r \in \mathbb{R}$に置き換えることでスカラー倍が定義されます。

$$ r \otimes \mathbf{x} = \frac{ (1 + \Vert \mathbf{x} \Vert)^r - (1 - \Vert \mathbf{x} \Vert)^r }{ (1 + \Vert \mathbf{x} \Vert)^r + (1 - \Vert \mathbf{x} \Vert)^r } \frac{\mathbf{x}}{\Vert \mathbf{x} \Vert} $$

双曲線関数/逆双曲線関数を使うとスカラー倍は実は

$$ r \otimes \mathbf{x} = \tanh \left( r \tanh^{-1} \left(\Vert \mathbf{x} \Vert \right) \right) \frac{\mathbf{x}}{\Vert \mathbf{x} \Vert} $$

と書くことも出来ます。この異様なほどの単純さは本論文中で、

$$ r \otimes \mathbf{x} = \exp_0 (r \log_0 (\mathbf{x})) $$

という事実を証明することで説明されます。これによりMöbius gyrovector spaceと双曲空間のRiemann幾何学が見事に関係しました！！

他にもgyrovector spaceにおいては$n$点の中点を定めることが出来たり（後述のHyperbolic Attention Networksはこの事実に依拠してHyperbolic Attentionを構成します）、gyrovector spaceにおける$\mathbf{a}$と$\mathbf{b}$を結ぶ直線$\mathbf{\mathbf{a}}\oplus(\ominus(\mathbf{a})\oplus\mathbf{b})\otimes t \ (0 \leq 0 \leq 1)$は$\mathbf{a}$と$\mathbf{b}$ を結ぶ測地線（最短曲線）に一致したりというような美しい整合性があり、双曲空間の幾何学的な性質を見事に代数的に翻訳していることがわかります。

本記事ではMöbius gyrovector spaceを説明しましたが、Einstein gyrovector spaceなども構成でき（これはBeltrami-Klein modelにおけるgyrovectorの構成になります）、こちらは特殊相対論の代数的構造に対応するそうです。

Hyperbolic Neural Networksの構成

だいぶ横道にそれましたが、Hyperbolic Neural Networksの構成に戻ります。本論文では、下記のNNsのコンポーネントの双曲空間における対応物の構成を行います（演算に$c$というのがついていたりしますが、スケールを表しているだけなので、ここでは無視しても差し支えありません）。

1. softmax / multinomial logistic regression (MLR)
2. スカラー倍
3. 行列倍、activation関数、要素積
4. concat + 行列倍

softmax / multinomial logistic regression (MLR)

Neural Networksの最後に $softmax(\mathbf{A} \mathbf{x} - \mathbf{b})$とする部分の双曲化です（説明の都合でバイアスを引いた形にしています）。 識別したいクラスのインデックスを$k$とすると、各クラス$k$ごとに

$$p(y=y_k | x) \propto \exp( \mathbf{a}_k \cdot x - b_k)$$

というモデル化をすることに対応します。この双曲化にあたっては、下記の論文の手法に従います。

• G. Labenon+, "Hyperplane margin classifiers on the multinomial manifold", ICML2014

この論文にならい、下記のように式変形を行います。$b_k = \mathbf{a}_k \cdot \mathbf{p}_k$とかける場合、

\begin{align} p(y=y_k | x) &\propto \exp( \mathbf{a}_k \cdot x + b_k) \\ &= \exp( \Vert \mathbf{a}_k \Vert sign( \mathbf{a}_k \cdot (- \mathbf{p}_k + \mathbf{x})) d \left(\mathbf{x}, {\mathbf{y} | \mathbf{a}_k \cdot (\mathbf{y} - \mathbf{p}_k) = 0 }\right) \end{align}

上記を双曲化するには、下記のようにvector演算をgyrovector演算に置き換えます（ついでにノルム$\Vert \mathbf{a}_k \Vert$も計量に合わせます）。

\begin{align} p(y=y_k | x) &\propto \exp( \mathbf{a}_k \cdot x + b_k) \\ &= \exp( \sqrt{ g_{\mathbf{p}_k}(\mathbf{a}_k, \mathbf{a}_k)} sign( \mathbf{a}_k \cdot (-\mathbf{p}_k \oplus \mathbf{x} )) d \left(\mathbf{x}, {\mathbf{y} | \mathbf{a}_k \cdot (\mathbf{y} \ominus \mathbf{p}_k) = 0 }\right) \end{align}

これもちょっといかめしい式ですが、上記の論文に従って定式化した後、演算をgyrovectorのものに翻訳しただけです。

スカラー倍

これはgyrovector演算に従って$r \otimes \mathbf{x}$で定義します。先に言及したとおり、本論文の貢献の一つですが、gyrovectorにおけるスカラー倍はPoincaré ballにおいて$\log_0$で中心$0$における接空間に持ってきたあとにスカラー倍をし、最後に$\exp_0$で双曲空間に戻すことと等価になります。

行列倍、activation関数、要素積

線形変換、activation関数は、スカラー倍が接空間でのスカラー倍に対応する事実を真似て、

1. $\log_0$で中心$0$での接空間へ移行 $\mathbf{x} \mapsto \mathbf{y} = \log_0 (\mathbf{x})$
2. 接空間で行列倍 $\mathbf{y} \mapsto \mathbf{z} = \mathbf{A} \mathbf{y}$, $\mathbf{y} \mapsto \mathbf{z} = \mathbf \phi({\mathbf{y}}$)
3. $\exp_0$で双曲空間にもどす$\mathbf{z} \mapsto \exp_0(\mathbf{y})$

とすることで定義します。あとでRNN/GRUを定義するときに必要になりますが要素積などもこの流儀で定義します。 この行列倍、アクティベーション関数適用を$\mathbf{A}\otimes \mathbf{x}, \phi^{\otimes}(\mathbf{x})$と表します。

concat + 行列倍

concatのみをすることはあまりなく、 $$ \begin{array}{ll}(\mathbf{M}_1, \mathbf{M}_2) \end{array} \left( \begin{array}{l} \mathbf{x}_1 \ \mathbf{x}_2 \end{array} \right) = \mathbf{M}_1 \mathbf{x}_1 + \mathbf{M}_2 \mathbf{x}_2 $$ というようにほぼ常に行列演算と組み合わせて扱われるので、こちらの双曲化を行いますが、これもgyrovector演算に置き換えて

$$\mathbf{M}_1 \otimes \mathbf{x}_1 \oplus \mathbf{M}_2 \otimes \mathbf{x}_2 $$

とします。

---

上記の構成により、多くのFeed Forward Neural Networksは双曲化することが出来ます。本論文ではその他、RNN/GRUも下記のように双曲化しています。

Naïve RNN:

GRU:

本論文ではSNLIという二文間の含意推定タスク（"little kids A. and B. are playing soccer" => "two children are playing outdoors"が真かなど）とToyタスクに適用して本構成がユークリッド空間での構成に比べてアドバンテージがあるかを調べています。圧倒的に優位というわけではないですが、ほぼ同様かときには優位な結果を得ています。

個人的にはgyrovector spaceと双曲空間のRiemann幾何の関係性を示したところ（ほかにもLevi-Civitaに関しても両理論の対合を示しています）がハイライトでした。双曲空間におけるNNsの構成はこの構成が唯一ではなく、もっと他の構成もありそうです。

Hyperbolic Attention Networks

本論文もgyrovector spaceの理論に依拠した構成をしています。 本論文が提案するのは、attention $$ \sum_i \frac{\alpha_j}{\sum_j \alpha_{ij}} \mathbf{v}_{ij} $$ の双曲化です。上記をそのままgyro演算にして $$ \oplus_i \frac{\alpha_j}{\sum_j \alpha_{ij}} \otimes \mathbf{v}_{ij} $$ としてもよいのですが（$\oplus_i$は$i$に渡るgyrovector和です）、この場合、どういう意味で重み付き平均をとっているのかの解釈が問題になります。

そのため、本論文ではEinstein gyrovector spaceにおける中点（Einstein midponit）のとり方をならうことで、より筋の通った双曲化を試みています。

Einstein gyrovectorにおけるvector $\mathbf{x}_1, \mathbf{x}_2, \cdots, \mathbf{x}_n$ の中点は、 $$ \sum_{i=1}^n \frac{\gamma(\mathbf{x}_i)}{\sum_j \gamma(\mathbf{x}_j)} \mathbf{x}_i $$ と定義されます（$\gamma(\mathbf{x})=1/\sqrt{1 - \Vert x \Vert^2}$は点$\mathbf{x}$に関するLorentzファクターと呼ばれる定数です）。

一応理論的な背景を説明しておくと、二点$\mathbf{a}$と$\mathbf{b}$の中点は、$\mathbf{a}$から$\mathbf{b}$へ向かう線分の 中点$\mathbf{m}_{\mathbf{a}, \mathbf{b}} = \mathbf{a}\oplus(\ominus\mathbf{a}\oplus\mathbf{b})\otimes\frac{1}{2}$として定義されます。これは明示的に

$$\mathbf{m}_{\mathbf{a}, \mathbf{b}} = \frac{\gamma(\mathbf{a}) \mathbf{a} + \gamma(\mathbf{b}) \mathbf{b}}{\gamma(\mathbf{a}) + \gamma(\mathbf{b})} $$

と計算されます。この式からも明らかですが$\mathbf{m}_{\mathbf{a}, \mathbf{b}} = \mathbf{m}_{\mathbf{b}, \mathbf{a}}$となるので、中点は二点の順番によらずに定義される概念です。これを延長して$n$点$\mathbf{a}, \mathbf{b}, \cdots, \mathbf{c}$の中点を

$$\mathbf{m}_{\mathbf{a}, \mathbf{b}, \cdots \mathbf{c}} = \frac{\gamma(\mathbf{a}) \mathbf{a} + \gamma(\mathbf{b}) \mathbf{b} + \cdots + \gamma(\mathbf{c}) \mathbf{c}}{\gamma(\mathbf{a}) + \gamma(\mathbf{b}) + \cdots \gamma(\mathbf{c})} $$

とします。本論文で提案されたattentionはこれを敷衍したものです。 なお、Einstein gyrovector spaceは双曲空間のBeltrami-Klein modelに対応するgyrovector spaceなので、双曲空間の他のモデルで扱いたい場合には、それらのモデル間の等長写像を用いて変換をおこいます。

本論文ではこのhyperbolic attentionの構成に加えて、Hyperboloid modelにおける点を

$$ (\mathbf{d}, r) \in \mathbb{R}^{n+1} \mapsto (\sinh(r)\mathbf{d}, \cosh(r))$$

という具合にパラメータ付けることにより、ユークリッド空間とHyperboloid modelの間の移行を提案しています。これにより、必要な部分だけhyperbolic attentionを行い、他の部分は通常の（Euclideanな）NNsとして処理することが可能になります。

本論文では、こうして定義されたhyperbolic attentionをQuestion AnsweringやMachine Translationなどのタスクに適用して通常のattentionに比べた優位性を確認しています。

attentionの定義の仕方はgyro的にも自然ですし、ユークリッドとHyperboloid modelの間の移行も簡単で実用的だと感じました。

Poincaré Glove: Hyperbolic Word Embeddings

本論文はユークリッド空間における埋込手法であるGloveを双曲空間に拡張定義しています。Gloveでは

$$ J = \sum_{i,j} f(X_{i,j})\left(\mathbf{u}_i \cdot \mathbf{v}_j + b_i + c_j - \log X_{ij} \right)^2$$

という形の目的関数の最小化を行いますが、上記を下記のように変形します。

$$ J = \sum_{i,j} f(X_{i,j})\left( -\frac{1}{2} \Vert \mathbf{u}_i - \mathbf{v}_j \Vert^2 + b'_i + c'_j - \log X_{ij} \right)^2$$

ここで、$b'_i = b_i + \Vert \mathbf{u}_i \Vert^2, c'_j = c_j+ \Vert \mathbf{v}_j \Vert^2$です。これの双曲化は

$$ J = \sum_{i,j} f(X_{i,j})\left( -\frac{1}{2} d(\mathbf{u}_i, \mathbf{v}_j)^2 + b'_i + c'_j - \log X_{ij} \right)^2$$

とします。ユークリッド距離を双曲空間における距離に置き換えただけです。本論文ではこれをやや修正して、ユーザー定義（ハイパーパラメータ）の関数$h(\cdot)$を導入して

$$ J = \sum_{i,j} f(X_{i,j})\left( -h( d(\mathbf{u}_i, \mathbf{v}_j)) + b'_i + c'_j - \log X_{ij} \right)^2$$

を提案しています。

本論文で言及されていて個人的に興味深かったのは、2つのガウス分布のあいだのフィッシャー情報距離が、それらの平均、分散を座標する2点間の上半空間モデルにおける距離に対応することです（既存研究）。2次元のときは下記のような対応です。

n次元のときは下記のとおりです。

この対応を考えると、双曲空間への埋め込みはガウス分布としての埋め込みとも思うことが出来ます。

分布間の包含（というか重なり合い）関係が双曲空間の木的な構造と関係しているというのは非常に印象的です。

まとめと感想

全体的にちょっと重たい解説になってしまいましたが、それくらい最近の双曲空間での機械学習が熱いことが伝われば幸いです。

双曲空間は、Riemann幾何とgyrovector spaceのような代数構造とが整合し、さらには情報幾何とも関係するきれいで実用的な空間です。

Riemann幾何的には座標不変な（座標のとり方に依存しない）性質を取り扱うのが本質的なので、原点（中心０）での接空間を考えたりするのは筋悪という考え方もあるかもしれません。Möbius gyrovector spaceもMöbius変換による原点0の写像を考えていることになるため、原点を意識した理論です。

このあたり、理論と実用がどう折り合って解釈されていくのか、これからも動向を探っていきたいです（原点を考えるのは座標不変性を考えると奇妙かもしれませんが、逆にどこでも中心と考えてよいのであれば原点を中心に据えてしまうのは悪くないのかもしれません）。

双曲空間におけるNeural Networksの構成もまだ開拓中な感が強いため、よりうまい構成を考えられれば、双曲空間はDeep Learningにおける非常に強力な武器になるかもしれません。

また、今回は説明しなかったですが、gyrovector spaceには通常の和$\oplus$の他にcoaddition $\boxplus$という演算もあります。$\boxplus$は$\oplus$と双対な関係にある演算で、実はMöbius gyrovector spaceやEinstein gyrovector spaceのようなgyro可換という性質をもつgyrovector spaceは、$\boxplus$が可換（$\mathbf{a} \boxplus \mathbf{b} = \mathbf{b} \boxplus \mathbf{a}$）になるという非常によい性質があります。$\boxplus$を使ったHyperbolic NNsの構成もありえそうなので考えてみたいと思います。

宣伝

きたる2019年3月4日、3月5日の2日間、東京品川駅「グランドプリンスホテル新高輪 国際館パミール」で2Days' AIカンファレンス「ABEJA SIX 2019」を開催します。 six.abejainc.com

私も「Deep Learningの都市伝説と現実」というタイトル（ちょっと大げさですが）でDeep Learning Lifeの振り返り・整理的な話をさせていただきます。

製造業やインフラ、流通小売業など様々な業種で、AI・機械学習をどのように活用しているか、実事例やそのためのノウハウを多数ご紹介する2DAYSカンファレンスです。 Day1はディベロッパーデイ。ぜひ技術者の皆様にお越しいただきたい日です。Day2はビジネスデイ。代表 岡田による基調講演に始まり、多くの実事例が公開されます。 ぜひご来場ください。

毎度ながら、ABEJAではイケててヤバい人材を探しています。

ABEJAが発信する最新テクノロジーに興味がある方は、是非ともブログの読者に！

ABEJAという会社に興味が湧いてきた方はWantedlyで会社、事業、人の情報を発信しているので、是非ともフォローを！！ www.wantedly.com

ABEJAの中の人と話ししたい！オフィス見学してみたいも随時受け付けておりますので、気軽にポチッとどうぞ↓↓