ABEJA Tech Blog

中の人の興味のある情報を発信していきます

トップ > 欠損, 非同期, 不規則な時系列データのモデリング - Neural CDEs の理論の導入部と実装

欠損, 非同期, 不規則な時系列データのモデリング - Neural CDEs の理論の導入部と実装

こんにちは！ABEJAでデータサイエンティストをしている藤原です。今年の4月に新卒で入社しました！

個人的な趣味で、少し前から「Neural Differential Equations」という分野の勉強を少しずつしているのですが、その中で「Neural Controlled Differential Equations」という研究が面白いなと感じました。そこで、理論の勉強だけじゃなく実際に動かしてみよう！と思い、今回は「Neural Controlled Differential Equations」について、前半では理論の導入部を、後半では具体的な実装と併せて紹介します。

今回の説明や実験で使っている実装の一式は GitHub - flatton/using_NeuralCDE_with_diffrax にて公開しています。

目次

はじめに

理論については Patrick Kidger 氏の博士論文 On Neural Differential Equations [1] を読みながら勉強しており、本記事においても主にその論文を参考にお話しします。また、実装については同氏が開発されたライブラリ Diffrax や Equinox など主に使用しています。*1

あらかじめ補足しておくと、この記事では Neural Differential Equations のソルバーや自動微分、誤差逆伝播については詳しく触れません。Neural Differential Equations の導入的な話と、 Neural Controlled Differential Equations というモデルの理論の導入部と実装方法について紹介します。*2

前提知識の補足：微分方程式（Differential Equations）

Neural Differential Equations の論文を読み始めた時に、そもそも微分方程式の知識や英語の用語が分からずに困った部分もあったため、同じような方の役に立てばと思いこのセクションを書いていますが、詳しい方にはこの部分の説明は不要かと思います。むしろ、私の理解が間違っている可能性があるため、その際はご指摘ください。

前提として、微分方程式（Differential Equations）について、後段の説明で出てくる数式や用語などを簡単に整理しておきます。

まずは微分方程式の例ですが、例えばこういうものです。

\displaystyle \frac{\mathrm{d}y}{\mathrm{d}t}(t) = f(t, y(t))

（ f：ベクトル場）

この形式の微分方程式は常微分方程式（Ordinary Differential Equations）と呼ばれるもので、Neural DEs の研究としておそらく最も有名な論文 Neural Ordinary Differential Equations [2] でベースになっている微分方程式です。

次に、初期値問題についてですが、微分形式と積分形式の表現方法があります。論文ではどちらの形式も登場するので、同じものであることさえ把握しておけば良いかと思います。 y(0) = y_0 は初期条件と呼ばれます。

初期値問題

次は、微分方程式の数値解法（ソルバー; solver）についてです。最も基本的な数値解法であるオイラー陽解法（explicit Euler method）について、簡単に触れておきます。

微分方程式を数値的に解くということは、初期値 x_0 から始めて、 x_1 = x_0 + h, x_2 = x_1 + h, ... における y(x) の値を順次求めていくことに対応します。このときの h を刻み幅と呼びます．[4]

オイラー陽解法では、次式によって解を計算していきます。

\displaystyle y_{j+1} = y_j + h f(t_j, y_j)

詳しく見てみると、 y_{j+1} が現在のステップの解で、それを得るために一個前のステップの解と y_j とステップ間での変化量（＝「刻み幅（ステップサイズ; step size） h」 \times 「傾き \frac{\mathrm{d}y}{\mathrm{d}t}(t) = f(t, y(t))」 ）を加算しています。 h を十分小さくすると精度は高くなりますが、計算時間が増えるなどの問題が発生します。*3

ひとまず、最低限の用語や背景知識としては以上です。

Neural Differential Equations; Neural DEs

Neural DEs とは？

次は、Neural DEs とは何か？ですが、「ニューラルネットワークを使ってベクトル場をパラメータ化した微分方程式」という解釈で良いと考えています。これだけだと分かりにくいかと思うので、微分方程式として記述してみます。 まず、通常の微分方程式はこうでした。

\displaystyle \frac{\mathrm{d}y}{\mathrm{d}t}(t) = f(t, y(t))

次に、Neural DEs ではこのように表記されます。

\displaystyle \frac{\mathrm{d}y}{\mathrm{d}t}(t) = f_\theta(t, y(t))

Neural DEs の式は、右辺のベクトル場 f に添え字がついています。つまり、ベクトル場 f をパラメータ化し、学習データによって最適化することで f を近似するのが Neural DEs ということになります。

また、ベクトル場をパラメータ化する方法ですが、大きく分けると次の2つのパターンに分けられます。

  1. ベクトル場をニューラルネットワークでパラメータ化して、学習によって最適化することでベクトル場本体を近似する。
  2. 元の微分方程式にニューラルネットワークでパラメータ化した補正項を追加し、理論値と実測値の誤差を小さくする。

（解釈が間違っているかもしれませんが、）正確な解を得るための計算量が膨大な微分方程式の場合は1、比較的少ない計算量である程度正確な解が得られる微分方程式の場合は2の方法でモデル化する、といった使い分けが存在していると思われます。

微分方程式とニューラルネットワークの関係

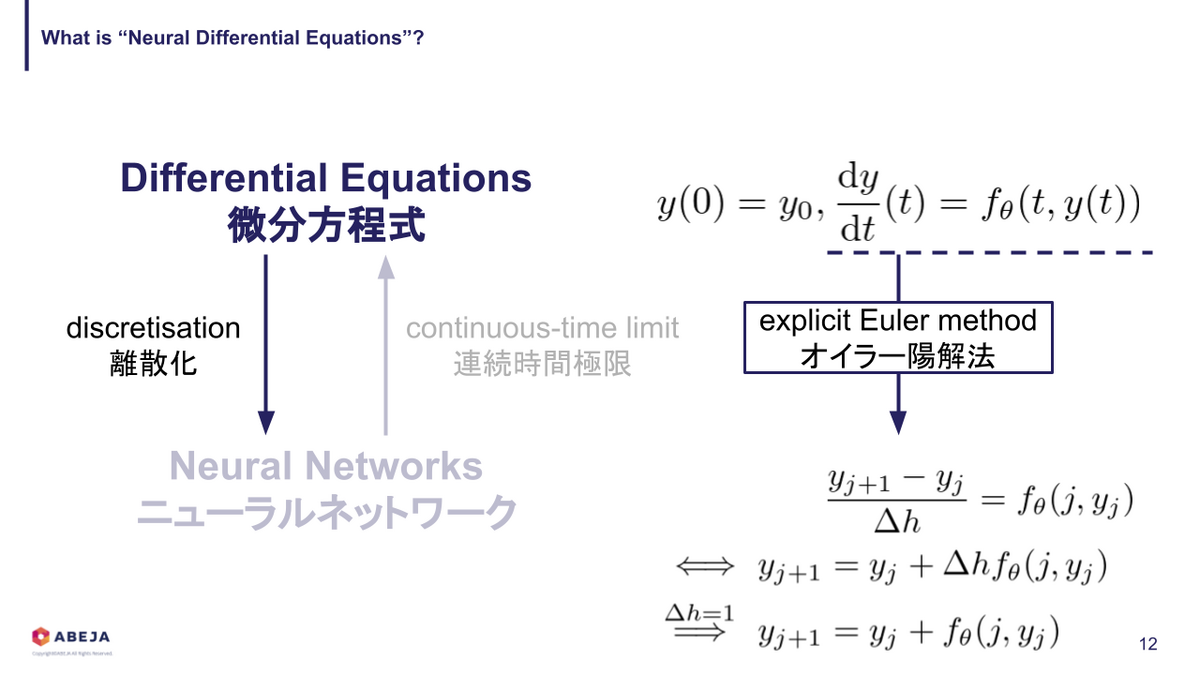
次に、なぜ微分方程式をベースにモデル化するか？という観点の話に触れておきます。この問いに対する最初の回答は「大成功している深層学習モデルは適切な微分方程式を離散化した形になっている」 [1] から、というのが一番魅力的な回答だと個人的には思っています。微分方程式を離散化したらニューラルネットワークになるとはどういうことか、先ほどの Neural ODEs を例に説明していきます。

おさらいすると、 Neural ODEs はこのように表現されます。

微分方程式の離散化 - 1

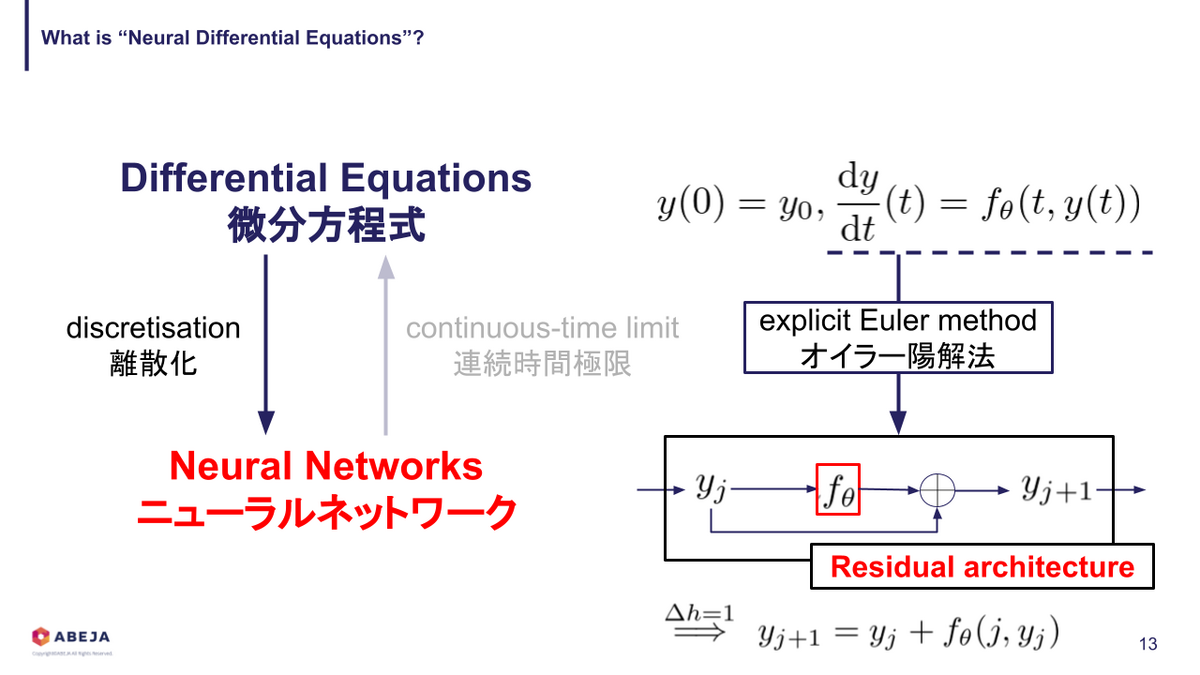
これをオイラー陽解法（explicit Euler method）で離散化 [4] すると、このように書けます。

微分方程式の離散化 - 2

すると、一番最後の方程式は残差構造の式になっていることが分かります。

微分方程式の離散化 - 3

このように、微分方程式とニューラルネットワークを互いに対応付けて考えることができます。

Neural DEs のメリット・デメリット

主なメリットとしては、次の二つがあるようです。

古典的な微分方程式の文献と比較すれば Neural DEs は全く前例のないモデリング能力を持つし、現代の深層学習の文献と比較するれば Neural DEs は「何が良いモデルを作るのか」についての理論を提供してくれる。 [1]

前者は、前述の通り計算コスト削減や実測値と理論値の差を埋めるといった点でメリットがあるということです。後者は、「良いモデルのどの要素が良いモデルたらしめているか？」を理論的に解釈できるという点でメリットがあるということです。私自身は後者に関心を持ち Neural DEs を勉強しています。

一方で、デメリットについても少し触れておきます。メリットの部分で「現代の深層学習モデルよりも精度・速度で優っている」といった記述がない点とも対応しますが、現状の Neural DEs のモデルは基本的に、（それを離散化した同系統の）ニューラルネットワークと比べて速度・精度の総合評価で勝るのは難しいものと思われます。後半に記載する実験では、学習時のメモリ使用量・処理時間、最終的な精度を比較していますが、どの項目でもニューラルネットワークの方が優れているという結果になりました。*4*5

ということで、あくまでモデルを開発する時に「条件に適した理論的に良いモデルとは何か？」という一つの視点として Neural DEs は貢献してくれます。もちろん、一部のケースではニューラルネットワークよりも良い性能を達成していますし、今後研究が進むことで処理時間やメモリ使用量の問題は改善される可能性があるため、実応用については今後の研究に期待しましょう！

Neural Controlled Differential Equations; Neural CDEs

ここからがメイントピックの Neural CDEs の話です。初めは理論的な部分を簡単に紹介し、後半はJAXベースの実装と併せてその仕組みを見ていきます。

Neural CDEs とは？ 〜Neural ODEs との違い〜

Neural CDEs とは時系列モデルのRNNの連続時間極限となっています。RNNと対応するモデルなので、時系列データを扱うためのモデルになっています。とはいえ、前述した Neural ODEs にも時刻を表すような変数 t が入っており、なぜ Neural ODEs ではダメなのか？という話にもなるかもしれません。そこで、まずは Neural ODEs と Neural CDEs を比較して、なぜ Neural CDEs か？を簡単に説明できればと思います。

まずは、 Neural ODEs の式をもう一度見てみましょう。

Neural ODEs について

少し用語の補足も入れていますが、 Neural ODEs はこのような式で表されていました。式を読み解くと、 t = 0 の時の入力 y_0 = y(0) が与えられると、任意のステップ t の 状態 y(t) が決定することが分かります。そのため、現在の構造では時系列のデータを扱える形式になっていません。

そこで、時系列のデータを扱える構造にするために、Ordinary Differential Equations ではなく Controlled Differential Equations をベースに再度 Neural DEs を構成します。

Neural ODEs と Neural CDEs の比較 - 1

Neural ODEs と Neural CDEs の違いは赤い丸で囲んでいる部分で、 Neural CDEs は x によって駆動される Controlled Differential Equations をパラメータ化したものです。時系列を受け入れられる構造になっているかどうかは、Neural ODEs と Neural CDEs の離散化した式を比較する方が分かりやすいかと思います。

Neural ODEs と Neural CDEs の比較 - 2

つまり、 Neural ODEs は x(0) が与えられると任意のステップの y(t) が決定しますが、 Neural CDEs では任意のステップの y(t) を決定するにはそのステップまでの入力 x(t) が必要な構造になっています。

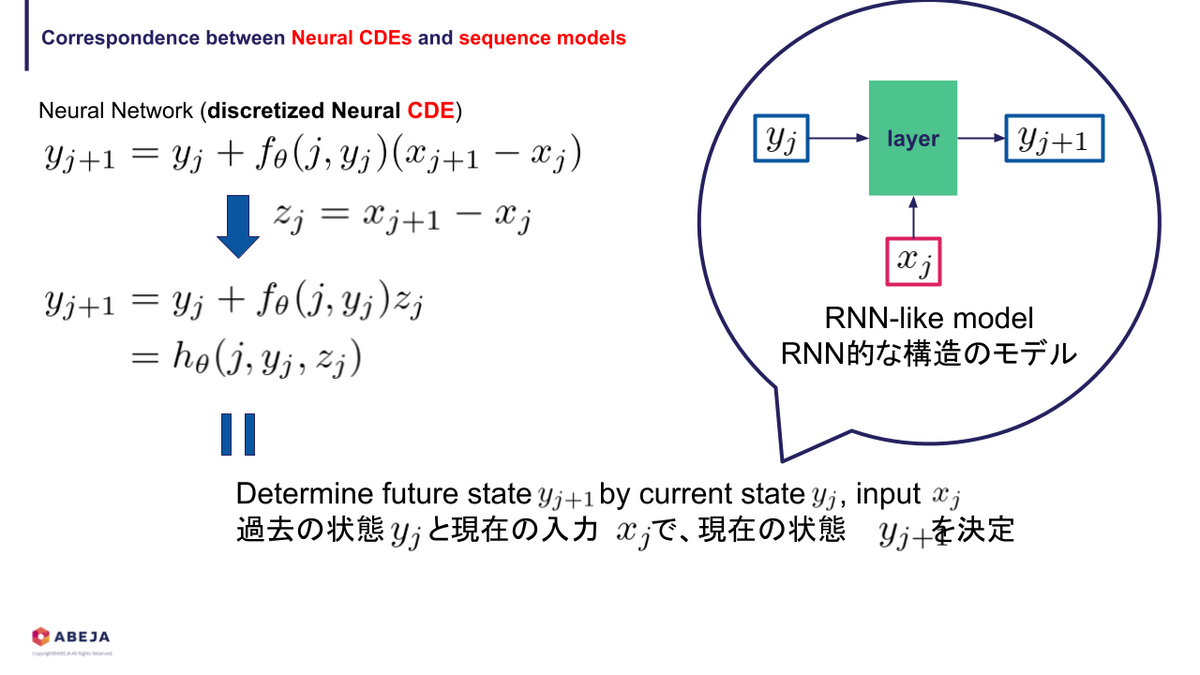
そして、この Neural CDEs は RNN ライクな構造を表現しています。

RNNとの関係

Neural CDEs と RNN の関係をもう少し掘り下げてみます。まずは、次のように式変形することで、RNNライクな構造のニューラルネットワークを構成できることがわかります。

Neural CDEs と RNNs の関係 - 1

今度は、離散化して得られた方程式の連続時間極限を取って、再度 Neural CDEs に戻してみましょう。

Neural CDEs と RNNs の関係 - 2

これで、RNN系統のモデルと Neural CDEs の関係性がイメージしやすくなったかと思います。なぜ連続時間極限をとってわざわざ Neural CDEs に戻したのか？は、次に書く Neural CDEs の特徴に関係しています。

Neural CDEs の特徴

まずは、 Neural CDEs の良い点からお話しします。一気に3つ書いていますが、まとめるとタイトルにあるように欠損値がある、チャネル間でサンプリリングレートが異なる（非同期）、サンプリングレートが一定でない（不規則）な時系列データを規則的なデータと同様に扱うことができます。

Neural CDEs の特徴 - 1

なぜ不規則なデータと規則的なデータが同様に扱うことができるか？ですが、これはそもそも Neural CDEs が連続的な入力を要求するところに関係します。実世界で計測されるデータは必ず離散的なものになりますが、 Neural CDEs では連続的なデータが必要になります。どうするかというと、補間（Interpolation）を行うことで連続的なデータ（パス; path）に変換します。

この補間処理の影響で、欠損値があったり、サンプリングレートが不規則であったりしても、 Neural CDEs へ入力される前に同じように連続的なパスに変換されます。また、チャネル間で非同期であっても、十分長い時間 T を取ってチャネル毎に連続的なパスに変換すれば、どのチャネルも任意の時刻 t \in [0, T) で値を持つ連続的なパスに変換することができます。そのため、 Neural CDEs では規則的なデータも不規則なデータも同じように処理することが可能となっています。

今度は、 Neural CDEs の欠点についてお話しします。Neural DEs に共通のデメリットは前半でお話ししているので、ここでは Neural CDEs 特有のデメリットのみお話しします。

一つ手前のセクションで、 RNNライクなモデル構造の方程式から連続時間極限を取ることで Neural CDEs を再構成していました。その時に得られた Neural CDEs の方程式を微分形式に変換します。

Neural CDEs の特徴 - 2

すると、 -y(t) という項が出てきました。これは GRU や LSTM でも同じような項が現れます。ここに注目すると、これは指数関数になっており、そしてこれは RNN 系統のモデルで隠れ状態の情報が指数関数的に減衰し、長期的な依存関係を学習できないことに対応しているようです。[1]

デメリットのお話しではありましたが、このようにニューラルネットワークの構造的利点・問題点を理論的に解釈できるのは Neural DEs の面白いところだと思います。ちなみに、この指数関数的減衰は長い系列の時に問題になるわけですが、これを克服するための手法 [5] もすでに研究されています。*6

実装を交えた説明

ここまでは理論的な話が続いていたので、ここからは実装と合わせてどのような仕組みになっているか見ていきます。

補間（Interpolation）

まずは、 Neural CDEs で重要な要素の一つである補間からお話ししていきます。 微分方程式で記述される通り、Neural CDEs では連続的な入力データを要求します。しかしながら、実際に観測されるデータは常に離散的なデータになっています。補間することで離散的なデータ ( \mathbf{x} = (x_0, \dots, x_n) ) を 連続的なパス ( x_\mathbf{x}: [0, T] \rightarrow \mathbb{R}^{d_x} ) に変換し、 Neural CDEs に入力できるようにします。

補間の手法もいくつか存在しており、シンプルな方法だと線形補間を使用する方法があります。線形補間では、サンプル点間を直線で補間するためサンプル点の位置で不連続なパスになります。（同時にベクトル場もサンプル点の位置で不連続になります。）不連続な点が含まれていると、数値積分が少し難しくなってしまうため、大域的に滑らかなパスが得られる補間が望ましいケースも多く存在します。

論文 [6] では、補間手法の比較をしており、詳しくはそちら（と論文 [1]） をご参照いただければと思いますが、論文 [1] の著者曰く、

できる限り「後方差分エルミート3次スプライン（Hermite cubic splines with backward differences）」*7を使うべきで、リアルタイム処理などの一部の場合では線形補間を利用すると良い。 [1]

という使い分けになっているようです。実装と合わせて見ていきましょう。

diffrax を用いて実装する場合、後方差分エルミート3次スプラインの補間を得るには主に次のクラス・メソッドを使用します。

  1. diffrax.CubicInterpolation
  2. diffrax.backward_hermite_coefficients

1 の diffrax.CubicInterpolation が補間クラスになっており、

\displaystyle d[i * (t - ts[i]) ** 3 + c[i] * (t - ts[i]) ** 2 + b[i] * (t - ts[i]) + a[i] ]

という式で、時刻 ts[i] から ts[i + 1] の補間を計算します。そのため、補間を得るためにはタイムスタンプの系列 ts と各時刻における係数 coeffs = (d, c, b, a) を事前に計算しておく必要があります。この係数を算出するために後方差分エルミートの係数算出メソッド diffrax.backward_hermite_coefficients を使用します。

具体的な使い方は下記のようになります。 ys は時系列データで (データ数, 各データの系列長, チャネル数) という形状のデータです。以下のコードでは、（系列長のバラバラな）一個一個の時系列データに対して diffrax.backward_hermite_coefficients を適用して係数 _coeffs を求め、最終的に coeffs = (d, c, b, a) という形状の係数データが得られるように整形しています。

func_interpolation = diffrax.backward_hermite_coefficients

coeffs = [[], [], [], []]
dim_ys = ys[0].shape[-1]
for _ts, _ys in zip(ts, ys):
    _coeffs = func_interpolation(_ts, _ys, fill_forward_nans_at_end=True, replace_nans_at_start=jnp.zeros(dim_ys))
    for i in jnp.arange(4):
        coeffs[i].append(_coeffs[i])
    coeffs = tuple(coeffs)

得られた係数を用いて、補間 diffrax.CubicInterpolation を用いてタイムスタンプの時刻の値を算出すると、元の観測された値と概ね等しい値が得られるはずです。実際に確認した結果がこちらのノートブック 04_ununiformed_sequence_dataloader.ipynb になります。以下に一部を抜粋します。

i = 0

sample_ys = ys[i] # 観測された時系列データ
sample_ts = ts[i] # 時系列データのタイムスタンプ
sample_coeffs = (coeffs[0][i], coeffs[1][i], coeffs[2][i], coeffs[3][i]) # `diffrax.backward_hermite_coefficients` で算出した係数

interpolation = diffrax.CubicInterpolation(sample_ts, sample_coeffs)
values = jax.vmap(interpolation.evaluate)(sample_ts) # 補間

for t, y, v_interp in zip(sample_ts, sample_ys, values):
    print(f"{t}: {y} --> {v_interp}")

# タイムスタンプ: 観測値 --> 補間データ
0.014212670736014843: [ 0.01421267 11.          9.        ] --> [0. 0. 0.]
0.015212670899927616: [ 0.01521267 12.                 nan] --> [ 0.01521267 12.          2.6666675 ]
0.016212670132517815: [ 0.01621267 13.                 nan] --> [ 0.01621267 12.999999    5.3333325 ]
0.017212670296430588: [ 0.01721267 13.          8.        ] --> [ 0.01721267 13.          8.        ]
0.01821267046034336: [ 0.01821267 14.          8.        ] --> [ 0.01821267 14.          8.        ]

このデータは、(タイムスタンプ, x座標, y座標)の時系列データという形式になっており、上記の数値列の左端の列がタイムスタンプになっています。見比べてみると、補間から得られたデータでは、初期値が全て0になっていたり、欠損値が埋まっていたり違いがありますが、観測値に値がある部分はその値が保持されており、補間されたデータになっていることが確認できます。初期値が0になってしまっているのは、Diffrax のバグでこのIssueで既に指摘されており、修正PRもすでに作成されています。しかしながら、別のエラーが原因でまだマージされていないため、今回はバグを含んだまま実験を行っています。ご了承ください。

Neural CDEs

序盤で「 Neural DEs はニューラルネットワークを使ってベクトル場をパラメータ化した微分方程式」と説明していました。そのため、一見するとNeural CDEs に含まれているニューラルネットワークはベクトル場をパラメータ化した部分のみのようですが、実際には主に3つのニューラルネットワークブロック（MLP/全結合層）が内部に含まれています。 コードはこちら：tools/_model/neural_cde.py

初期値を生成するMLP

MLP自体はシンプルで、 Equinox の nn.MLP を使って下記のような形でモデルを定義しています。

initial = eqx.nn.MLP(in_size, out_size, width_size, depth, key=key)

in_size は入力層のノード数、out_size は出力層のノード数、width_sizeは隠れ層のノード数、depthは隠れ層の層数（出力層を含めてカウント）となっています。 key はJAXの仕様で乱数生成に使用されるキーです。JAXでは最初に jax.random.PRNGKey(seed) で生成したキーを jax.random.split で分割し、そのキーを使って乱数生成する必要があり、そのため key が必須の引数として設定されています。

この initial には何が入って何が出力されるのかというと、このように使用されます。

interpolation = diffrax.CubicInterpolation(ts, coeffs)
x0 = interpolation.evaluate(ts[0])
y0 = initial(x0)

つまり、パス x の初期時刻 0 における値を入力として、隠れ状態の初期値 y(0) を得るために使います。この y(0) は序盤で登場した初期値問題における初期条件に対応しています。*8

ベクトル場をパラメータ化したMLP

ここがメインの「ベクトル場をパラメータ化したニューラルネットワーク」のブロックです。早速、実装を見てみましょう。

class Func(eqx.Module):
    """Define vector fields.
    ベクトル場を定義.
    """
    mlp: eqx.nn.MLP
    in_size: int
    hidden_size: int

    def __init__(self, in_size: int, hidden_size: int, width_size: int, depth: int, *, key: PRNGKeyArray, **kwargs):
        super().__init__(**kwargs)
        self.in_size = in_size
        self.hidden_size = hidden_size
        self.mlp = eqx.nn.MLP(
            in_size=hidden_size,
            out_size=hidden_size * in_size,
            width_size=width_size,
            depth=depth,
            activation=jnn.softplus,
            # Note the use of a tanh final activation function. This is important to
            # stop the model blowing up. (Just like how GRUs and LSTMs constrain the
            # rate of change of their hidden states.)
            final_activation=jnn.tanh,
            key=key,
        )

    def __call__(self, t: Optional[Float[Array, ""]], y: Float[Array, "in_size"], args: Optional[Array] = None):
        """Calcurate the vector fields $$f_\theta(y_i)$$.
        ベクトル場の行列を算出.

        **Arguments:**
        - t: タイムスタンプ $$t_i$$
        - y: 隠れ状態 $$y_i$$
        
        **Returns:**
        - ベクトル場 $$f_\theta(y_i)$$
        """
        return self.mlp(y).reshape(self.hidden_size, self.in_size)

中身も至ってシンプルで、前述の equinox.nn.MLP を使ってMLPを定義しています。インスタンス化した Func オブジェクトを呼び出すと __call__ 内の処理が実行され、MLPを通じて次のステップの隠れ状態が計算されると共に、reshape によってデータの形状が変形されます。データの形状を変形する理由は、簡単な理解としては積分系の Neural CDEs をイメージすると良いです。

\displaystyle y(t) = y(0) + \int_{0}^{t} f(y(s)) \mathrm{d}x(s)

これを見ると、少なくとも y(0) と足し合わせるために積分の項の結果は隠れ状態の次元数のベクトルになっている必要があります。さらに、 \mathrm{d}x(s) の部分は入力パスの次元数のベクトルになるため、 f(y(s)) の部分は (隠れ状態の次元数のベクトル, 入力パスの次元数) という形状の行列である必要があります。そのため、reshape によってデータの形状を変形しています。*9より具体的な視点は、少し後の Neural CDEs 離散化したニューラルネットワークの実装でお話しします。

隠れ状態から出力値を生成するための全結合層

最後のニューラルネットワークブロックは、隠れ状態から出力値を生成するための全結合層で、これは通常のニューラルネットワークと同様の構造です。実装としても、最終ステップ T における隠れ状態 y(T) を、線形層 eqx.nn.Linear と、Cross Entropy Loss 用の出力層の活性化関数 jax.nn.log_softmax を通すだけです。

linear = eqx.nn.Linear(hidden_size, out_size, key=lkey) # 出力層のモデルを初期化
activation_output = jnn.sigmoid if out_size == 1 else jnn.log_softmax

probs = activation_output(linear(solution.ys[-1]))

solution.ys が各タイムステップにおける隠れ状態の系列になっているので、その終端の値を取って線形層と活性化関数に通している形です。

Neural CDEs 全体の実装について

あまり詳しく話すとキリがないので、記事には記載しませんが、 Diffrax で微分方程式を解く部分の実装については 01_controlled_differential_equations.ipynb や tools/_model/neural_cde.py を参考にしていただければと思います。

前述で作成した3つのニューラルネットワークブロックと、微分方程式＆ソルバーのブロックをまとめて Neural CDEs モジュールとして定義すれば、通常のニューラルネットワークのように学習・推論させることができます。そのほか、ソルバー・補間の選び方など、手法に選択肢がある場合は大抵 Diffrax のドキュメント・コメントに参考になる情報が書かれているため、困ったときは Diffrax の中で検索してみてください。

Neural CDEs をオイラー陽解法で離散化した RNNライクなニューラルネットワーク

今度は、Neural CDEs をオイラー陽解法で離散化した RNNライクなニューラルネットワーク（以下、離散化 Neural CDEs）について、実装をみていきます。（tools/_model/discrete_cde.py）といっても、基本的な構成は Neural CDEs と同様で、3つのMLP/全結合層のブロックが含まれており、処理のフローとしても基本的に同じです。実装もできる限り Neural CDEs と見比べやすいように、ある程度体裁を揃えています。

大きく違う部分は、（当然ですが）オイラー陽解法で離散化することで得られたRNNライクな構造の部分です。ここについて細かく見てみましょう。

RNNライクな構造のニューラルネットワークブロック

まず、Neural CDEs と同じくベクトル場 Func が使用されています。ベクトル場が使用されているのは DiscreteCDECell の中で、この DiscreteCDECell は y_{j+1} = y_j + f(y_i) (x_{j+1} - x_j) という計算をするモジュールになっています。 Neural CDEs の部分で、なぜベクトル場の出力を reshape しているか簡単に触れましたが、 yi1 = yi0 + h_f @ (xi1 - xi0) を見ると、より具体的にその理由が理解できるかと思います。

class DiscreteCDECell(eqx.Module, strict=True):
    mlp: Func

    def __init__(self, input_size: int, hidden_size: int, width_size: int, depth: int, use_bias: bool = True, dtype=None, *, key: PRNGKeyArray, **kwargs):
        super().__init__(**kwargs)
        self.mlp = Func(input_size, hidden_size, width_size, depth, key=key)

    def __call__(self, xi: Float[Array, "* input_size"], yi0: Float[Array, "hidden_size"], *, key: Optional[PRNGKeyArray] = None) -> Float[Array, "hidden_size"]:
        xi0, xi1 = xi
        h_f = self.mlp(None, yi0)
        yi1 = yi0 + h_f @ (xi1 - xi0)
        return yi1

ということで、 DiscreteCDECell のモジュールで、 Neural CDEs の離散化で得られる構造が実装できているので、残りは大した処理はありません。残りの DiscreteCDELayer はどちらかというと、JAXのための実装という節もあります。

class DiscreteCDELayer(eqx.Module):
    cell: DiscreteCDECell

    def __init__(self, input_size: int, hidden_size: int, width_size: int, depth: int, *, key: PRNGKeyArray, **kwargs):
        super().__init__(**kwargs)
        self.cell = DiscreteCDECell(input_size, hidden_size, width_size, depth, key=key)

    def __call__(self, y0: Float[Array, "*sequence_length hidden_size"], xs1: Float[Array, "*sequence_length input_size"], *, key: Optional[PRNGKeyArray] = None) -> Tuple[Float[Array, "hidden_size"], Float[Array, "*sequence_length hidden_size"]]:
        def _f(carry, xs):
            carry = self.cell(xs, carry)
            return carry, carry
        xs1 = jnp.expand_dims(xs1, axis=1)
        xs0 = jnp.zeros_like(xs1)
        xs0 = xs0.at[1:, :, :].set(xs1[:-1, :, :])
        xs = jnp.concatenate([xs0, xs1], axis=1)
        yT, ys = lax.scan(_f, y0, xs)
        return yT, ys

このモジュールで行っている処理は

  1. 変化量 x_{j+1} - x_j の算出のために、xs1, xs0 を作成

  2. ループ処理の高速化のために lax.scan を使用し、隠れ状態の計算を実行

となっています。このモジュールへの実行時の入力は初期の隠れ状態 y0 と、入力パス xs1 で、出力は終端の隠れ状態 yT と各タイムステップでの隠れ状態の系列 ys です。ということで、これで 離散化 Neural CDEs の完成です。

では最後に、これらを実際に動かして Neural CDEs と離散化 Neural CDEs を比較してみます。

実験

実験概要

Neural CDEs と離散化 Neural CDEs を学習/推論時のメモリ使用量・実行時間、評価データに対する正解率で比較します。メモリ使用量は memrayを使用して測定しており、ピークメモリ使用量で比較を行います。

前置き

以下の内容について、ご承知ください。

実験環境について

  • ノートPC上の Jupyter Lab で実験を行っており、メモリ消費量や処理時間の測定において不安定な結果になっている可能性があります。

実験条件について

  • 学習はエポック数を固定しており、今回の実験条件では Loss が完全に収束していない可能性があります。
  • 実験は各条件について1回の試行しか実施しておりません。
  • Neural CDEs とその離散化となるニューラルネットワークを正確に比較するには、使用する数値解法（ソルバー）に合わせてニューラルネットワークの構造を変化させる必要があるかと思いますが、本実験ではその部分の整合性は取っておりません。数値解法は利用したライブラリのノートブックで使用されている、かつ、推奨されているものを使用しました。*10

その他

  • diffrax のバグがあり、一部の処理が正常ではありません。（修正PRはすでに作成されているのですが、別の何らかのエラーが原因でまだマージされていないため、今回はバグが残った状態で実験を実施していることをご了承ください。）

実験データ

今回は、手書き数字データセット MNIST の画像を解析して作成された、ピクセルの位置からなる書き順の系列データを使用します。[7]*11このデータセットには、書き順の表現方法がいくつかあるのですが、今回はシンプルな二次元のピクセルの位置 (x, y) の系列で表現された書き順データを使用します。

また、Neural CDEs の特徴として、「サンプリングレートが一定でない、欠損値がある、チャネル間で非同期でも良い」というのがあるので、この特徴を評価できるようにデータを加工します。まずは、「サンプリングレートが一定でない」の部分ですが、この書き順データには元よりタイムスタンプなどないので、ペンの移動時間が前のピクセルから現在のピクセルへの移動距離に比例すると仮定して、一定でないがある程度自然な（気がする）タイムスタンプを作成しています。詳しくは MNISTStrokeDataset._make_timestamp を参照ください。残りの「欠損値がある、チャネル間で非同期でも良い」の部分は、ピクセルの位置の系列データにランダムなマスクを施すことで作成しています。同時に、非同期なデータを再現するために、x座標の系列とy座標の系列に同じ1次元系列のマスクを適用するのではなく、(x座標, y座標)の系列に2次元系列のランダムなマスクを適用しています。こちらも詳しくは MNISTStrokeDataset._random_mask_nan を参照ください。

その他の実験条件

実験は主にノートブック 10_mnist_experiment.ipynb を使用して実施します。

  • データ量
    • 学習データ：60,000
    • 評価データ：10,000
  • Optimizer：Adam
  • lr：1e-3
  • Batchsize：32
  • Iteration：10,000 （固定）
  • モデルサイズ
    • out_size：10
    • hidden_size：16
    • width_size1：28

実験結果

実験結果を表にまとめるとこうなりました。

NeuralCDE 離散化NeuralCDE
0% drop 50% drop 0% drop 50% drop
Training Processing Time [sec. / iter.] 1.07 2.03 0.02 0.15
Peak Memory Usage 5.8 GiB 5.7 GiB 4.1 GiB 4.6 GiB
Inference Processing Time [sec. / sample] 0.0086 0.0083 0.0029 0.0028
Peak Memory Usage 2.6 GiB 2.75 GiB 1.5 GiB 2.3 GiB
Scores Accuracy [%] 93.0 83.6 95.9 87.9
Cross Entropy Loss 0.232 0.549 0.135 0.412

0% drop, 50% drop はデータの欠損率で、各時系列データに対してランダムにマスクした値の割合を示しています。*12見比べてみると、今回の比較方法だといずれの項目でも 離散化NeuralCDE（RNN）の方が Neural CDEs よりも軽くて早くて性能も良いという結果になっています。ただし、正解率については、イテレーション数や学習率を調整すると Neural CDEs の方が高くなる可能性はあります。学習にかなり時間がかかるので、実用的にみると現状は気軽に使えるモデルではないというのも事実かと思います。データの欠損率が高いと処理時間やメモリ使用量が増えるのは、補間処理の影響があると考えられます。

まとめ

今回は、Neural DEs について導入的な話をするとともに、Neural CDEs というモデルの理論の導入部と実装方法について紹介しました。また、実際に Neural CDEs とその離散化にあたるニューラルネットワークを比較し、実用上の課題について実際に動かして把握することができました。冒頭で述べた通り、 Neural DEs はニューラルネットワークの構造の理論的な理解に役立つものなので、今後も少しずつ勉強していく予定です！

We Are Hiring!

ABEJAは、テクノロジーの社会実装に取り組んでいます。 技術はもちろん、技術をどのようにして社会やビジネスに組み込んでいくかを考えるのが好きな方は、下記採用ページからエントリーください！ （新卒の方のエントリーもお待ちしております）

careers.abejainc.com

参考文献

[1] Kidger, Patrick. "On neural differential equations." arXiv preprint arXiv:2202.02435 (2022).

[2] Chen, Ricky TQ, et al. "Neural ordinary differential equations." Advances in neural information processing systems 31 (2018).

[3] Kidger, Patrick, et al. "Neural controlled differential equations for irregular time series." Advances in Neural Information Processing Systems 33 (2020): 6696-6707.

[4] 微分方程式の数値解法 - 東京大学工学部 精密工学科 プログラミング応用 I・ II

[5] Morrill, James, et al. "Neural rough differential equations for long time series." International Conference on Machine Learning. PMLR, 2021.

[6] Morrill, James, et al. "Neural controlled differential equations for online prediction tasks." arXiv preprint arXiv:2106.11028 (2021).

[7] Edwin D. de Jong, "MNIST sequence data", https://edwin-de-jong.github.io/blog/mnist-sequence-data/

*1:JAXでニューラルネットワークを実装するのに Equinox は良いライブラリだと思います。

*2:余談ですが、はじめに Neural DEs の勉強をしようと思った時に論文・記事を検索してみると、"Neural Ordinary Differential Equations"の論文やたくさんの解説記事が出てきました。ただ、それらの解説記事を読んでもよく分からず、もっと基礎から勉強しようと思った結果、Patrick Kidger 氏の博士論文 [1] を読み始めたという経緯があります。そして、Neural CDEs まで読み進めてようやく Neural ODEs についてもモヤモヤしていた部分が解消されました。そのため、本記事では Neural CDEs についてお話しすることで、ある程度充実している Neural ODEs の解説記事と併せて、Neural DEs全体への理解を深めるのに役立てていただけると幸いです。

*3:また、オイラー法では一階微分の値までしか使用していないため近似の精度が十分ではなく、より近似の精度が高い様々なソルバーが存在しています。ソルバーの選び方についても Diffrax にドキュメントがあるため、気になる方はご参照ください。

*4:ノートPCなど不安定な環境ではなくサーバ上などで実験する、開発データへの精度が収束するまで学習させるなど実験条件が公平にする、数回の実験を行い平均する、などを行えば結果が変わるところも出てくるかもしれません。また、実験データが複雑になれば Neural DEs のモデルの方が優れた結果が得られるかもしれません。

*5:メモリ使用量については比較する微分方程式/ニューラルネットワーク次第で変化する部分があります。論文[2]で述べられているように、Neural ODEsと一般的な残差ネットワークで比較すればNeural ODEsの方がメモリ消費量を抑えることができます。何を揃えて比較するか、という実験条件次第だと思われます。

*6:キーワードは Neural Rough Differential Equations, log-ODE method, Rough path theory, Signatures, Logsignatures あたりです。私自身 Neural RDEs の方も Appendix に書かれている理論を読みましたが、そもそもラフパス理論やシグネチャをよく知らないので全然ピンときませんでした。「CDEをテイラー展開し、その際に出てくるシグネチャからいくつかの理論的なテクニックで入力データの冗長性を排除する」みたいなイメージで理解していますが、よく理解できていません。ただし、いくつか限界もあると論文に書いてありました。

*7:（適切な訳・解釈ができていないかもしれませんが、）区分3次エルミート補間（Piecewise Cubic Hermite Interpolating Polynomial; PCHIP）を指していると思われます。

*8:ただし、補間のところで少し触れた通り、バグのせいで補間後の初期値は全て0になっており、毎回同じy0が得られてしまうため、今回の実装だと上手く機能していません。

*9:ただし、これはCDEをODEに帰着させた時の解法であり、それができるのはパスが連続で微分可能な場合です。

*10:ソルバーの選び方の参考: https://docs.kidger.site/diffrax/usage/how-to-choose-a-solver/#how-to-choose-a-solver

*11:論文[3] では、アルファベットの書き順データセットが使用されています。

*12:50%より大きい値に設定すると、適応的に数値積分のステップサイズが調整されるアルゴリズムになっている関係で、ステップサイズが足りなくなり(?)エラーになる。詳細は原因不明。

Page Top
  • Copyright © ABEJA, Inc. All rights reserved.