ABEJA Tech Blog

中の人の興味のある情報を発信していきます

トップ > コンペで使える！？LightGBMで実装する３つの弱教師あり学習

コンペで使える！？LightGBMで実装する３つの弱教師あり学習

ABEJAでデータサイエンティストをしている小林です。 今回は、もしかしたらいつか業務や機械学習コンペに役立つかもしれない情報、LightGBMで弱教師あり学習を行う方法についてお話します。

コードはこちらで公開しております。

目次

はじめに

機械学習を行うためには、一般的に、大量の入力データと、それら一つ一つに対応した正確なラベルが必要です。 例えば、犬と猫の画像分類を行う場合には、それぞれの画像一つ一つに犬か猫のラベルがついていてほしいですね。

一方で場合によっては、一つ一つのデータに対しては正確なラベルが手に入らない場面もあるかもしれません。

例として、Kaggleのコンペ"Human Protein Atlas - Single Cell Classification"を見てみましょう。 このコンペのタスクは、人の細胞の画像を入力として、細胞の種類を分類することでした。

www.kaggle.com

このコンペの特徴的な点は、ラベルの与えられ方でした。 通常「一つ一つの細胞の分類」を行う設定では、それぞれの細胞一つ一つが何の細胞であるか？のラベルが与えられていることが多いですね。 これは教師あり学習と呼ばれる設定です。 一方このコンペでは、一つ一つの細胞に対するラベルの代わりに、複数の細胞が写った画像に対して「何の種類の細胞が含まれているか？」のラベルのみ与えられていました。 そのため参加者は、この複数の細胞に対するラベルの集合から工夫を凝らして、一つ一つの細胞を分類する必要がありました。*1

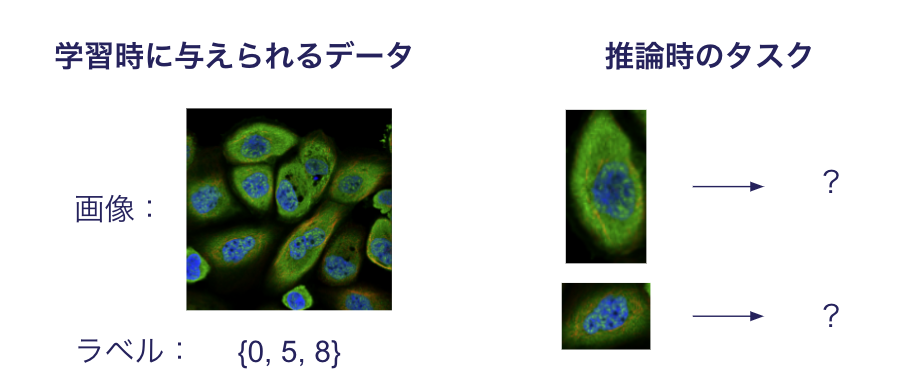
複数のラベルを含む画像を学習データとし、各細胞のラベル１つずつを予測するコンペ

このように限られた情報から分類問題を行う分野は、弱教師あり学習（Weakly Supervised Learning）と呼ばれています。

弱教師あり学習の例（マルチインスタンス学習）

弱教師あり学習とは一般的に、限られた情報から分類を行う手法のことを指し、さまざまな設定が含まれます。

例えば、マルチインスタンス学習（Multiple Instance Learning）と呼ばれる二値分類の設定では、一つ一つのデータ（インスタンス）の集合であるバッグに対して、 「バッグの中に１つでも正例が含まれるかどうか？」のラベルがついています。

マルチインスタンス学習については、以下の記事が分かりやすいです。 こちらの記事では特に、深層学習モデルを用いてマルチインスタンス学習を行う、Attention MIL*2と呼ばれる手法を紹介しています。

tech.preferred.jp

LightGBMで弱教師あり学習がしたい！

最近、大規模な汎用モデルが画像・自然言語・音声などの分野で次々と登場してますね。 一方で、データがそれぞれ違った意味を持つことの多いテーブルデータにおいては、画像・自然言語・音声とは異なり、このような汎用モデルは存在しません。 そのためテーブルデータでは、アノテーション過程を含む学習データの準備を経て、自前の機械学習モデルを（決定木モデルなどを用いて）作成する必要があることが多いです。

このような状況を鑑みると、なんだかテーブルデータにこそ弱教師あり学習が必要な気がしてきますね？ 特に、テーブルデータのデファクト・スタンダードである、決定木モデルを用いて弱教師あり学習を行ってみたいですよね？

決定木モデルで弱教師あり学習を行う際に気をつけたい点として、 決定木モデルに適用可能なのは勾配を用いた学習法であり、特定のモデル構造や特徴量学習などの学習法を適用できないということです。 例えば上記の記事で紹介されている、"Attention MIL"のようにモデルの構造に依存する手法は、LightGBMなどの決定木モデルには適用できません。

LightGBMに適用可能な手法

そこで本日は、LightGBMにも適用可能な「勾配を用いた学習」を行う手法、特に教師あり学習の損失を変形して用いる手法を、いくつかの弱教師あり学習の設定とともに紹介していきます。

PU分類

問題設定

ここでは、迷惑メールの分類を考えてみましょう。

この分類を行うにあたって、それぞれのメールが迷惑メールかどうか？の情報が必要ですね。 迷惑メールかどうか？のラベルを自動作成するに当たって、今回はユーザーの報告を用いることにします。

いま、ユーザーが迷惑メールと報告したものについては、それが迷惑メールであると断定できます。 一方で報告されなかったメールについては、もしかしたらユーザーが報告しなかっただけかもしれませんから、迷惑メールかもしれませんし、通常のメールかもしれません。

ユーザーの報告を元に取得されるデータセット

改めて状況を整理してみます。 迷惑メールを正例、普通のメールを負例としましょう。 このとき、入手できたデータセットは２種類あり、正例（ユーザーに報告された迷惑メール）と正例と負例（ユーザーに配信されたメールの全て）と言うことができます。

このように、手元のデータが正例データ（Positive）とラベルなしデータ（Unlabeled）から二値分類を行う設定をPU分類と言います。

解き方

ここでは、教師あり学習の損失式を変形する手法を紹介します。*3 変形の目的は教師あり学習の損失を、「正例データ」と「正例と負例（ラベルなし）データ」の2種類のデータセットから推定できるように分解することです。


\begin{align}
R(f) &= \int_{x} \sum_{y} p(x, y) \ell(f(x), y) dx \\
&= \int_{x} p(x, y=+1) \ell(f(x), +1) + p(x, y=-1) \ell(f(x), -1) dx \\
&= \int_{x} p(x, y=+1) \ell(f(x), +1) + (p(x) - p(x, y=+1)) \ell(f(x), -1) dx \\
&= \int_{x} p(x, y=+1) (\ell(f(x), +1) - \ell(f(x), -1)) + p(x) \ell(f(x), -1)  dx \\
&= p(y=+1) \int_{x} p(x| y=+1) (\ell(f(x), +1) - \ell(f(x), -1)) dx + \int_{x} p(x) \ell(f(x), -1)  dx \\
&=(\text{正例データの割合}) \times (\text{正例データを正例とみなした損失}) \\
&- (\text{正例データの割合}) \times (\text{正例データを負例とみなした損失})) \\
&+ (\text{ラベルなしデータを負例とみなした損失})
\end{align}

頑張って式変形することで、教師あり学習の損失を「正例データ」と「ラベルなしデータ」から推定できる損失の和に変形できました！ 中身を見てみると、次の3種類の損失を推定して、重みづけた和を取っていることが分かります。

  • 正例データを正例とみなした損失
  • 正例データを負例とみなした損失
  • ラベルなしデータを負例とみなした損失

「正例データを負例とみなした損失」を計算するって、なんだか不思議ですよね。

式だけでは本当に学習ができるか、実感がわきませんね。実装・実験を行ってみましょう！

LightGBMの実装

上の式では、各正例・ラベルなしデータセットに対して期待値を取っていますが、LightGBMでは「１つの入力に対して１つの出力」を計算する必要があります。

では、この損失をLightGBMで実装してみましょう。

１つの入力に対する損失を取り出してみると、次のように書くことができますね。

（正例の場合）


(\text{正例データの割合}) \times ((\text{正例データを正例とみなした損失}) -(\text{正例データを負例とみなした損失}))

（ラベルなしデータの場合）


(\text{ラベルなしデータを負例とみなした損失})

これを、LightGBMのカスタム損失で実装してみましょう！ LightGBMのカスタム損失では、各入力に対して勾配（gradient）と二階微分（hessian）を計算して出力する必要があります。 ここではpu_lossで損失を計算し、pu_loss_objectiveでscipyの数値微分を用いて勾配と二階微分を計算します。 詳しい実装はgithubをご参照ください。

def pu_loss(x: np.ndarray, t: np.ndarray, positive_ratio: float):
    """
    Args:
        x (np.array): モデルの出力配列
        t (np.array): ラベルの配列
        positive_ratio (float): 正例データの割合

    Returns:
        np.array
    """
    # sigmoid関数
    p = 1 / (1 + np.exp(-x))
    #
    loss_positive = (
        positive_ratio
        * (logloss(p) - logloss(1 - p))
        * (t == 1)
        / (t == 1).sum()  # 平均を取る
    )
    loss_unlabeled = logloss(1 - p) * (t == -1) / (t == -1).sum()  # 平均を取る
    return loss_positive + loss_unlabeled


def pu_loss_objective(y_pred:np.ndarray, trn_data:lgb.Dataset):
    """PU分類の損失の勾配を計算"""
    y_true = trn_data._pu_label
    partial_fl = lambda x: pu_loss(x, y_true, positive_ratio=0.5)
    grad = derivative(partial_fl, y_pred, n=1, dx=1e-6)
    hess = derivative(partial_fl, y_pred, n=2, dx=1e-6)
    return grad, hess

実験

設定

実験では、PCAで次元圧縮したMNISTデータセットを用いました。奇数を正例、偶数を負例として扱います。 正例の割合は0.5を既知として与え、正例のみからなる1000枚のデータセットと、そのほか正例と負例を含むデータセットを準備しました。

PU分類の実験設定

結果

検証用データに対する正解率曲線は以下のグラフのとおりです。 教師あり学習ほどではありませんが、ランダムな性能が50%程度であることを考えると、ある程度の性能で学習できていることが分かります。

正解率曲線（PU分類）

Partial Label Learning

問題設定

ここでは、１つのデータに複数のラベルが付いており、そのうち１つだけが正しい場合を考えましょう。 MNISTの分類で例えると、「１」に対して、「１か、２か、７か」のようにラベルが付いているような状況です。*4

PLLの設定のイメージ。１つの物体に（答えを１つ含む）複数のラベルがついている。

冒頭で紹介したKaggleコンペの例を思い出してみましょう。 このコンペでは、細胞の集合に対して、それに対応するラベルの集合が与えられているのでした。 そのため、一つ一つの細胞に着目すると、複数の細胞ラベルが付けられているとみなすこともできるため、Partial Label Learningの設定とみなすこともできますね！

解き方

ここでも、教師あり学習の損失式を変形する手法を紹介します。*5 いま、データxに対するラベルをy、データxに与えられた複数のラベルの集合をYとします。 このとき教師あり学習の損失は、以下のように変形することが可能です。


\begin{align}
R(f) &= \int_{x} \sum_{y} p(x, y) \ell(f(x), y) dx \\
&= \int_{x} \sum_{y} \sum_{Y} p(x, y, Y) \ell(f(x), y) dx \\
&= \int_{x} \sum_{y} \sum_{Y} p(x, Y) p(y | x, Y) \ell(f(x), y) dx \\
&= \int_{x} \sum_{y} \sum_{Y} p(x, Y) \frac{p(y,Y | x)}{p(Y|x)} \ell(f(x), y) dx \\
&= \int_{x} \sum_{y} \sum_{Y} p(x, Y) \frac{p(y,Y | x)}{\sum_{y} p(y,Y|x)} \ell(f(x), y) dx \\
&= \int_{x} \sum_{Y} p(x, Y) \sum_{y \in Y} \frac{p(y| x)}{\sum_{y \in Y} p(y|x)} \ell(f(x), y) dx \\
&= (\text{全てのラベル候補}y \in Y\text{について}p(y|x)\text{で重みづけた損失})
\end{align}

この式変形から、p(y|x)を用いて、教師あり学習の損失をデータxとラベル集合Yから推定できることが分かりました。 次に、p(y|x)をどのように推定するかですが、論文ではモデルの前回の予測値を用いる逐次的なアップデートが提案されています。

モデルと重みの更新

LightGBMの実装

では、この損失をLightGBMで実装してみましょう。 先程説明したようにこれを実装するためには、 p(y|x) の推定値を保存しておく必要があります。

ここでは、LightGBMの学習に用いるクロスエントロピー損失の勾配、二階微分を直接計算することにします。 これは例えばこちらの記事*6を参考にすると、次のように実装できます。

def pll_loss_objective(y_pred:np.ndarray, trn_data:lgb.Dataset):
    # Softmaxの計算
    ## p: num_sample x num_class
    p = softmax(y_pred.reshape(NUM_CLASS, -1).T)
    # 前回推論したp(y|x)を取り出す
    ## weight: num_sample x num_class
    Pyx = trn_data._pweight
    # マルチホットラベルのYを取り出す
    # Y: num_sample x num_class
    Y_mh = trn_data._partial_labels
    # 各ラベルに対する重みを計算する
    # gweight: num_sample x num_class
    gweight = Pyx * Y_mh
    # ワンホットラベルのYを計算する
    # Y_oh: num_sample x num_class x num_class
    Y_oh = Y_mh[:, None] * np.eye(NUM_CLASS)
    # 各ラベル候補に対して、重み付きの勾配、二階微分を計算する
    grad = ((p[:, None] - Y_oh) * gweight[..., None]).sum(1)
    hess = ((p * (1 - p))[:, None] * gweight[..., None]).sum(1)
    grad = grad.T.reshape(-1)
    hess = hess.T.reshape(-1)
    # 次回使用するP(y|x)を計算する
    new_Pyx = softmax(y_pred.reshape(NUM_CLASS, -1).T)
    # ラベル候補以外は0として、合計値で割る
    new_Pyx = new_Pyx * Y_mh
    trn_data._pweight = new_Pyx / new_Pyx.sum(-1, keepdims=True)
    return grad, hess

実験

設定

実験では、先程と同様にMNISTデータセットを用いました。各データにベルヌーイ分布からサンプリングしたラベルを付与します。

Partial Label Learningの実験設定

各インスタンスxに付与されているラベルの個数の分布は次のようになっています。 全てのインスタンスに複数のラベルが与えられている状態です。

PLLのラベル数

結果

正解率曲線を以下のグラフに示します。 全てのインスタンスに複数のラベルが与えられていたにも関わらず、教師あり学習と同じような正解率が出ています。ここまでの精度で学習ができるのはとても面白いですね。

正解率曲線（Partial Label Learning）

マルチインスタンス学習

問題設定

では最後に、マルチインスタンス学習について扱ってみましょう。 マルチインスタンス学習では、複数のデータ（インスタンス）の集合に対して、もし１つでも正例を含む場合、そのインスタンス集合には正例のラベルが与えられます。 最終的に行いたいタスクは二値分類で、一つ一つのインスタンスを分類します。

MILで与えられるデータのイメージ。正例を１つでも含むかどうか？がラベルとして与えられる。

冒頭で紹介したKaggleコンペの例は、Partial Label Learningの設定とみなすこともできました。 一方、ラベルが付けられた細胞クラスについて、この種類の細胞は、与えられた細胞集合の中に存在するというラベルだと捉えると、マルチインスタンス学習の設定ともみなすことができそうですね。

解き方

３回目ですが、教師あり学習の損失式を変形する手法を紹介します。*7 いま、インスタンス集合Xに対するラベルをY、データXに与えられた「インスタンス集合の中に正例を含むかどうか」を表す変数をsとします。 このとき教師あり学習の損失は、ほぼPartial Label Learningと同様にして、以下のように変形することが可能です。 ここでは、インスタンス集合内のi番目の要素を、上付き文字で表しています。


\begin{align}
R(f) &= \int_{x} \sum_{y} p(x, y) \ell(f(x), y) dx \\
&= \frac{1}{K} \int_{X} \sum_{Y} p(X, Y) \sum_{i=1}^{K} \ell(f(X^{(i)}), Y^{(i)}) dx \\
&= \frac{1}{K} \int_{X} \sum_{s} \sum_{Y} p(X, s) \frac{p(Y,s | X)}{\sum_{Y} p(Y,s|X)} \sum_{i=1}^{K} \ell(f(X^{(i)}), Y^{(i)}) dx \\
\end{align}

ここで、さらにマルチインスタンス学習の設定では次が成り立ちます。


P(s|X) =
\begin{cases}
\prod_{k} P(Y^{(k)} = 0| X^{(k)}) & (s=0) \\
1 - \prod_{k} P(Y^{(k)} = 0| X^{(k)}) & (s=1)
\end{cases}

このことから、i番目のインスタンスについて以下の関係を導出することができます。


\sum_{Y}P(Y, s=0 | X) =
P(Y^{(i)} = 0| X^{(i)}) \prod_{k \neq i} P(Y^{(k)}  = 0| X^{(k)})



\sum_{Y}P(Y, s=1 | X) =
P(Y^{(i)}=1| X^{(i)}) + P(Y^{(i)}=0| X^{(i)}) (1 - \prod_{k\neq i} P(Y^{(k)} = 0| X^{(k)}))

LightGBMの実装

では、この損失をLightGBMで実装してみましょう。 学習はPartial Label学習と同様に、重みP(y|x)の更新を用いて行います。

def mil_loss_objective(
        y_pred:np.ndarray,
        trn_data:lgb.Dataset,
        bag_size:int,
):
    # sigmoidの計算
    p = 1 / (1 + np.exp(-y_pred))
    ## s=0の条件下での重み。0列目がy=0の重み、1列目がy=1の重み
    ## weight0: num_sample x 2
    ## s=1の条件下での重み。0列目がy=0の重み、1列目がy=1の重み
    ## weight1: num_sample x 2
    weight_s0 = trn_data._weight_s0
    weight_s1 = trn_data._weight_s1
    # マルチインスタンス学習のラベルs (バッチ数)を取り出す
    s = trn_data._mil_labels

    # 各ラベルに対する重みを計算
    # ラベルyが0である場合の重み
    gweight_s0 = weight_s0[..., 0] * (s == 0) + weight_s1[..., 0] * (s == 1)
    # ラベルy=1である場合の重み
    gweight_s1 = weight_s0[..., 1] * (s == 0) + weight_s1[..., 1] * (s == 1)

    # 各ラベル候補に対して、重み付きの勾配、二階微分を計算する
    grad = p * gweight_s0 - (1 - p) * gweight_s1
    hess = p * (1 - p) * gweight_s0 + p * (1 - p) * gweight_s1

    # 次回使用する重みを計算する
    # 各インスタンスがy=0,1である確率をlogで計算
    ## logp0: num_instance x bag_size
    ## logp1: num_instance x bag_size
    logp0 = np.log((1 - p.reshape(-1, bag_size)) + 1e-12)
    logp1 = np.log(p.reshape(-1, bag_size) + 1e-12)
    # 自身を除いたバッグ内のlog確率の和
    weights_other_logp0 = np.tile(logp0[:, None], [1, bag_size, 1]).sum(-1) - logp0
    # s, yで条件づけた重みの計算
    weights_log_s0 = logp0.sum(-1)[:, None]
    weights_log_s1 = np.log((1 - np.exp(logp0.sum(-1)) + 1e-12))[:, None]
    weights_log_s0y0 = (logp0 + weights_other_logp0 - weights_log_s0).reshape(-1)
    weights_log_s1y0 = (
        logp0 + np.log(1 - np.exp(weights_other_logp0) + 1e-12) - weights_log_s1
    ).reshape(-1)
    weights_log_s1y1 = (logp1 - weights_log_s1).reshape(-1)
    # 重みの結合、保存
    weights_s0 = np.stack(
        [np.exp(weights_log_s0y0), np.zeros_like(weights_log_s0y0)], axis=-1
    )
    weights_s1 = np.stack([np.exp(weights_log_s1y0), np.exp(weights_log_s1y1)], axis=-1)
    trn_data._weight_s0 = weights_s0
    trn_data._weight_s1 = weights_s1
    return grad, hess

実験

設定

実験では、これまでと同様にMNISTデータセットを用いました。 4つのインスタンスでバッグを構成することとし、ラベルとしては数字の9を正例、それ以外を負例として扱います。

マルチインスタンス学習の実験設定

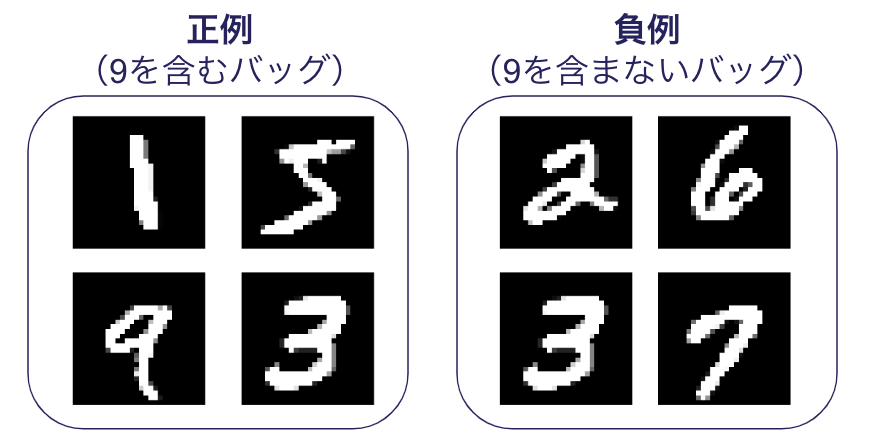
結果

検証用データに対する正解率曲線は以下のグラフのとおりです。こちらも、学習が進むごとに、分類がうまく行えてますね。

正解率曲線（Multi Instance Learning）

おわりに

このブログでは、3つの弱教師あり学習の設定・解き方と、そのLightGBMでの実装法を紹介しました。

もちろん、実務では正確なラベルを付けたり、データを増やしたりすることが重要になってくる場合も多いため、必ずしも役立つ分野ではないかもしれません。 一方で、もしかしたらこのような学習法を知っておくことでコンペや業務で役に立つかもしれませんし、身近な問題を新たな面白い視点から見ることができるかもしれませんね。

ABEJAではゆたかな世界を、実装する仲間を募集しています。気になった方は是非ご連絡ください。

careers.abejainc.com

*1:正確には細胞の検出も必要でしたが、これは公式の検出器も提供されていました。https://github.com/CellProfiling/HPA-Cell-Segmentation

*2:https://proceedings.mlr.press/v80/ilse18a.html

*3:https://papers.nips.cc/paper_files/paper/2014/hash/35051070e572e47d2c26c241ab88307f-Abstract.html

*4:ラベルの分布はデータに独立と仮定します

*5:https://proceedings.neurips.cc/paper/2020/hash/7bd28f15a49d5e5848d6ec70e584e625-Abstract.html

*6:https://tawara.hatenablog.com/entry/2020/05/14/120016

*7:https://arxiv.org/abs/2306.11343

Page Top
  • Copyright © ABEJA, Inc. All rights reserved.