　こんにちは、ABEJAの真壁孝嘉（@Takayoshi_ma）です。変数Aと変数Bにどれくらいの関連性があるの？このデータから何が言える？みたいなニーズって至る所にあるかと思います。その時に活用される様々な数学的指標たち、（自分含め）名前を知ってるだけだと危険だよなあって場面が近頃多い気がしたので、改めてメモ的な意味でブログを書いてみました。前半に（ピアソンの積率）相関係数に関する注意点を列挙したのち、後半にそれ以外の数学的指標の概要を列挙していこうと思います。

　尚、このブログで度々登場する相関係数とはピアソンの積率相関係数を表すこととします。

相関係数の注意点

相関係数の概要

　相関係数の定義式は以下になります。

$r = \dfrac{ s_{xy} }{ s_x s_y }$

$r = \dfrac{ xとyにおける共分散 }{ x における標準偏差 × y における標準偏差}$

　おそらく、このブログを読んでいる方の多くは既知の情報だと思いますが、簡単に説明をしておくと、分子の共分散を分母で割ることで取りうる範囲を $-1 ≤ r ≤ 1$ にしたのが相関係数となります。また共分散に関しては下のような図が有名かと思います。

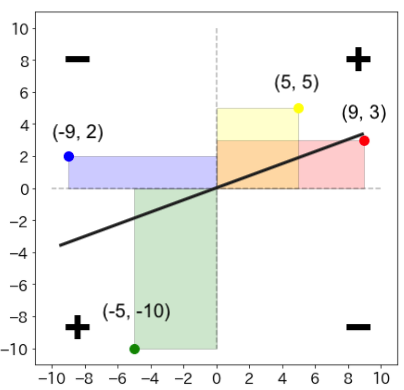
上記の例だと $s_{xy} = (-5 * -10) + (-9 * 2) + (5 * 5) + (9 * 3) = 84$ となります。図形的なイメージで捉えると分かりやすいですが、

$\bar{x}$ および $\bar{y}$ からより遠いデータの方が共分散に与える影響が大きい
上記グラフの右上or左下に多くのデータが集まれば共分散は $+$ 、逆は $-$ になる

となることが分かります。また、上記グラフにある直線は回帰直線を示していますが、こちらは必ず $(\bar{x}, \bar{y})$ を通ることが知られています。（比較的メジャーな事柄なので証明は省きます。）

相関関係と因果関係は異なる概念

　これもまあまあ良く出る話だと思いますが、両確率変数の相関係数が大きいからといって両者の因果関係が保証できるわけではありません。

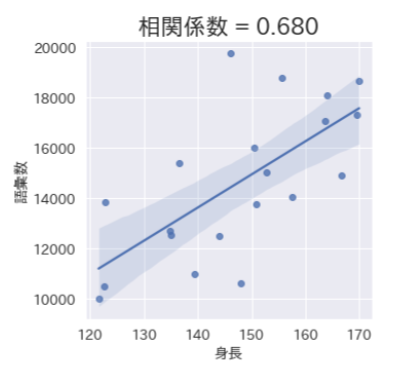
上図の例を見て、「背が高い方が語彙数も多く頭が良い」といった解釈は難しく、「背が高い」→「年齢が上」→「教育歴が多い」と考える方が自然かと思います。

尚、第3の変数の影響を共に除去した上で、2変数の相関をみる偏相関係数と呼ばれる指標や、一方から影響を除去した上で相関をみる部分相関係数と呼ばれる指標が存在します。

（ $y$ から $z$ の影響を除いたものと $x$ の部分相関係数）

$r\left[x, (y | z)\right] = \dfrac{ r_{xy} - r_{xz} r_{yz} }{\sqrt{ 1 - r^2_{yz} }}$

（ $y$ から $z$ の影響を除いたものと $x$ から $z$ の影響を除いたものの偏相関係数）

$r\left[(x | z), (y | z)\right] = \dfrac{ r_{xy} - r_{xz} r_{yz} }{ \sqrt{ 1 - r^2_{xz} } \sqrt{ 1 - r^2_{yz} }}$

無相関であることと、独立であることは異なる概念

　こちらも比較的よく出る話題ですが、相関関係がないからと言って、両変数の間に確率的な依存関係が全く無いとは言い切れません。よく例として同心円上に分布が広がった散布図があるかと思います。（無相関だけど、明らかに $x$ の値によって $y$ の事後確率も変わってくるよねっていう図）

このように直線の関係とは言えないもののその分布に何かしらの確立的依存性が見られるケースは多く存在します。

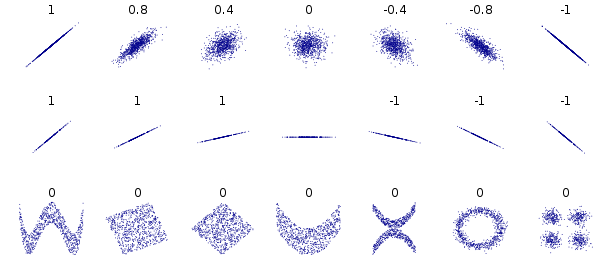
[相関係数 -Wikipedia より抜粋]

　逆に独立→無相関の証明ですが、比較的容易にできるのでここでは省略します。

相関係数は外れ値に影響されやすい

　共分散の説明でも触れた通り、 $\bar{x}$ および $\bar{y}$ からより遠いデータの方が共分散に与える影響が大きくなります。

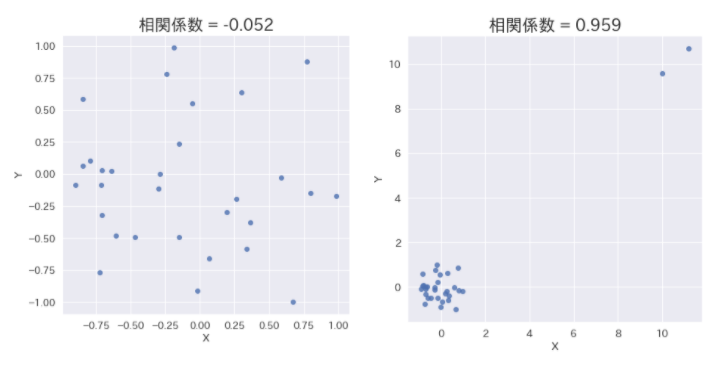
その影響もあり、外れ値が相関係数に与える影響はかなり大きくなってしまいます。上記例の場合データを2点追加しただけでその相関係数が大きく変わってしまっていることが確認できるかと思います。

選抜効果

　上記までと同じような理由で、相関係数には選抜効果と呼ばれる作用が存在します。

特進クラス（比較的成績上位グループ）と普通クラスを合わせて算出された相関係数と、それぞれ別のグループに分けた状態で算出された相関係数に差があることが分かります。このように相関係数にはあるスケールに限定してみていくとその値が小さくなる場合があります。

相関係数の標準誤差

　一般的な感覚として、ある母集団からサンプリングされた標本においてそのサンプル数が多いほど、標本統計量の信頼性は高くなる傾向があるのは理解できるかと思います。実際、相関係数もサンプル数が多いほど、母相関係数の信頼区間は狭くなっていく傾向があります。（後述）その逆も然りで、標本相関係数においてはデータ数が少なければ少ないほどその標準誤差も大きくなってしまう影響も頭の片隅に入れておいた方が良い場面もあります。

例として以下のようなシチュエーションをあげてみます。

例）日本全国の男性から40人をランダムにピックアップし、身長と体重の相関係数を算出した結果0.7だった。この時の母相関係数の95%信頼区間を求めよ

標本相関係数( $r$ )の分布はそのままだと扱いづらいのですが、フィッシャーの $Z$ 変換を用いることで正規分布に近似することができ、その扱いも簡易になることが知られています。（注：フィッシャーの $Z$ 変換が適用できるケースとして2変数、この場合身長と体重が共に正規分布であることが条件となってきます。ここから先はそれを仮定した話となります）

$z = tanh^{-1} r = \dfrac{1}{2} log \dfrac{1+r}{1-r}$

変換された $z$ の標準偏差は $\dfrac{1}{\sqrt{n - 3}}$ となるので、あとはよくある標準正規分布へ標準化した場合における区間表を利用した、信頼区間算出問題に落とし込めます。

ただし、上記手順で算出された値はあくまで $Z$ 変換後のものなので、こちらを逆変換して戻したものが求めるべき母相関係数の信頼区間となります。

$r = \dfrac{exp({2z}) - 1}{exp({2z}) + 1}$

# pythonでの計算例

r = 0.7
n = 40

z_low = ((1/2) * np.log((1 + r) / (1 - r))) - 1.96 * np.sqrt(1 / (n - 3))
z_high = ((1/2) * np.log((1 + r) / (1 - r))) + 1.96 * np.sqrt(1 / (n - 3))

r_low = (np.exp(2 * z_low) - 1) / (np.exp(2 * z_low) + 1)
r_high = (np.exp(2 * z_high) - 1) / (np.exp(2 * z_high) + 1)

print(f'r_low: {r_low:.3f}  r_high: {r_high:.3f}')

# r_low: 0.497  r_high: 0.830

上記の結果よりその95%信頼区間は0.48 - 0.83程度であることが分かりました。少ないサンプル数であった場合、おそらく感覚よりもその標準誤差が大きいことを感じれるかと思います。

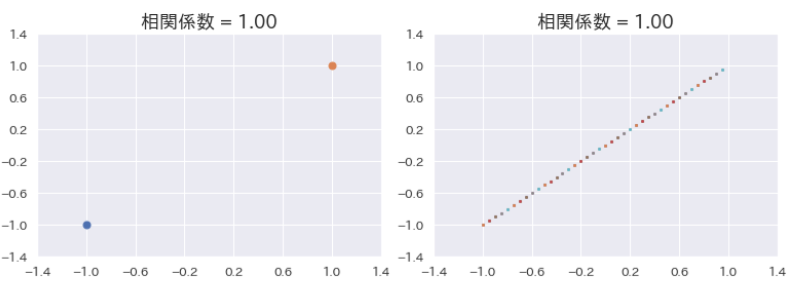
標本相関係数は母相関係数の不偏推定量ではない

　既に既出ですが、例え2変数が正規分布だったとしてもその標本相関係数の分布は正規分布とはなりません。またその平均も母相関係数の不偏推定量とはならないことが知られています。あくまでもイメージですが、

上記の例がしっくりくるかと思います。ここで母相関係数を $\rho$ とすると、得られる標本相関係数の平均は

$\mu_r = \rho - \dfrac{\rho (1 - \rho^2) }{2N}$

と近似できることが知られています。式を見てわかる通り、 $\rho=0$ または $|\rho| = 1$ の場合を除いて、標本相関係数の期待値は $\rho$ と一致しないことが分かります。第二項の分母にサンプル数 $N$ が存在しているので、これは $N$ を増やしていくと $\rho$ に近づく一致推定量ではありますが、サンプル数が少ないと比較的絶対値の小さな値が出やすいことがわかるかと思います。

2つの指標の関連度を測る指標の紹介

　ここから先は相関係数を一旦忘れて、それ以外に存在する二変数の関連度合いを示す指標を紹介していきたいと思います。これだけ色々あるにも関わらず、相関係数と比べると比較的マイナーな存在だと思いますが、色々知ることでケースバイケースで扱う武器も増えていく（はず）

コサイン類似度

　機械学習の文脈で登場することも多い類似度指標にコサイン類似度というものがあります。感覚的に伝えると確率変数が並んでいるベクトル同士の向きがどの程度似ているかを表した指標です。こちらは本質的に相関係数とほぼ変わりありません。

（ $x$ と $y$ の相関係数） $r = \dfrac{ s_{xy} }{ s_x s_y }$

（ $x$ と $y$ のコサイン類似度） $cos(\boldsymbol{x}, \boldsymbol{y}) = \frac{\boldsymbol{x}\boldsymbol{y}}{||\boldsymbol{x}||||\boldsymbol{y}||}$

式を見ていただくと分かりますが、 $\bar{x} = 0$ かつ $\bar{y} = 0$ のとき、その相関係数とコサイン類似度は一致することが分かります。

自己相関係数

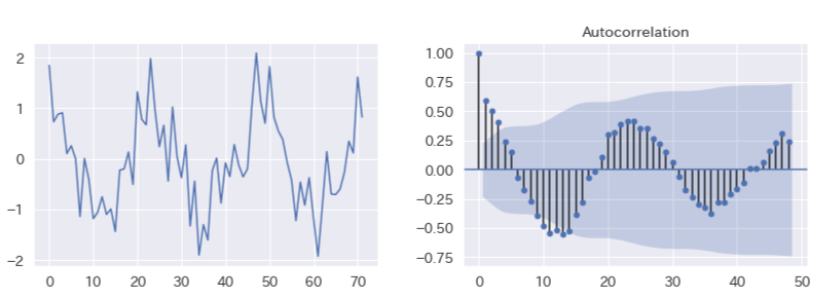
　異なる2つの確率変数の相関係数と違い、こちらは過去における自身と現在の自身がどの程度関連性があるかを示す指標になります。例えばラグが1の時の自己相関係数であれば、一つ前の自身との相関係数であり、ラグが24の自己相関係数であれば24個前の自身との相関係数になります。下記は手元で生成したデータのプロットとその自己相関係数をラグ毎に示した図（コレログラム）です。直前（ラグ1）との自己相関係数が最も高く、ラグ12の時は負に大きく、逆に24の時は正に大きな自己相関係数を示しています。

順位相関係数

　相関係数を扱う上で外れ値に弱いという点は見逃せない場面も多いと思います。また2変数の分布が正規分布とはほど遠い分布であったり、そもそも量的変数ではなく、質的変数（順序尺度）であったりする場合もあります。そのような2変数の関連度を測る指標として、データの大きさそのものではなく、その順位に着目する指標が存在します。特定の分布を仮定しないノンパラメトリックな手法であり、場合によってはよりロバストな指標と言えます。以下、順序尺度を基に算出される指標を挙げていきます。

スピアマンのρ

　こちらは式自体は（ピアソンの積率）相関係数と変わりません。違う点として、変数の値をそのまま使用するのでなく大きさ順に並び替えた順位を使って値を算出することにあります。

グッドマン・クラスカルのγ

　 $\boldsymbol{x}$ (length=n)と $\boldsymbol{y}$ (length=n)が与えられた時、 $0, 1, 2, ... n$ から $i$ と $j$ （ $i ≠ j$ ）を選ぶとき（つまり全ての組み合わせ数は $nC_{2}$ ）、 $K$ と $L$ を以下の様に定義します。

$K$ ： $x_i$ と $x_j$ 、 $y_i$ と $y_j$ の大小関係が一致する組みの数
$L$ ： $x_i$ と $x_j$ 、 $y_i$ と $y_j$ の大小関係が一致しない組みの数

例えば、度々事例として挙げている数学と英語の例であれば、Aさんの英語と数学の順位が共にBさんの英語と数学の順位より上であれば $K$ 、片方が上でもう片方が下のような状況であれば $L$ となります。これを全ての $i$ と $j$ で試して算出された $K$ と $L$ を用いて、以下のように計算された値がグッドマン・クラスカルのγになります。

$\gamma = \dfrac{K - L}{K + L}$

ケンドールのτ

　まずケンドールの $\tau_{a}$ ですが、先ほどまでの $K$ と $L$ を用いて以下の様に算出することができます。この後の説明がしやすいように敢えて先ほどの $\gamma$ と表現を変えていますが、直前のグッドマン・クラスカルの $\gamma$ と同じものになります。

$\tau_{a} = \dfrac{K - L}{nC_2}$

　次に $\tau_{b}$ ですが、こちらは先ほどまでの指標と違い同順位だった場合を考慮したものになります。 $x_i = x_j$ となる組数を $X_0$ 、 $y_i = y_j$ となる組数を $Y_0$ とした場合、 $\tau_{b}$ は以下の様に算出できます。

$\tau_{b} = \dfrac{K - L}{ \sqrt{nC_2 - X_0} \sqrt{nC_2 - Y_0} }$

同順位の組数が0の場合、既出の指標と同じ結果になることが分かると思います。

クロス集計表における関連度合いを示す指標

　カテゴリ変数同士の関連性を可視化するものとして代表的なものにクロス集計表があります。ここからはクロス集計表が与えられた際にその関連度合いを示す指標達について紹介していきます。

カッパ係数

　 $\kappa$ 係数の範囲は $-1 ≤ \kappa ≤ 1$ で、大きい方が一致度が強いとされています。 $\kappa$ 係数は名義尺度と順序尺度で適用される指標が変わってきます。

通常のカッパ係数（名義尺度）

　よく $\kappa$ 係数の具体例で出てくる様なマトリックスですが以下のような例を考えたいと思います。

	2人目の医師
1人目の医師	A	B	C	計
A	2	0	1	3
B	1	2	0	3
C	0	0	4	4
計	3	2	5	10

分かりやすいよう比率にします。（キリのよい数字なのであまり変わりませんが）

	2人目の医師
1人目の医師	A	B	C	計
A	0.2	0	0.1	0.3
B	0.1	0.2	0	0.3
C	0	0	0.4	0.4
計	0.3	0.2	0.5	1.0

　このマトリックスの対角線上が、両者の判定が一致した部分になります（8人）。つまり全体で $0.8$ の一致率と言えます。この時問題となるのが、2名の医師がデタラメに分類していたときに起こり得る一致を考慮に入れていないことです。仮にデタラメに分類していた場合の期待値は以下の通りになるかと思います。

1人目の医師も2人目の医師もAと判断する確率 = $0.3 × 0.3 = 0.09$
1人目の医師も2人目の医師もBと判断する確率 = $0.3 × 0.2 = 0.06$
1人目の医師も2人目の医師もCと判断する確率 = $0.4 × 0.5 = 0.20$

よって合計 $0.35$ が偶然に一致する期待値と言えます。

この時の $\kappa$ 係数は $\kappa = (0.8 - 0.35) / (1 - 0.35) ≒ 0.69$ となります。

重みづけカッパ係数（順序尺度）

　こちら順序尺度を比べる時に使用されます。例えば先ほどの例で $A$ , $B$ , $C$ が何かしらの順序変数であった場合、 $A$ を $B$ と間違えるよりも、 $A$ を $C$ に間違える方が良くないというのは直感に合っているかと思います。これを意図的に重み付けすることで評価したのが重み付けカッパ係数となります。また重みの定め方には様々な手法がありますが、二乗を使う場合が多くその場合の重み付けカッパ係数をquadratic weigted kappaと言います。

　まず始めに、先ほどのkappa係数同様、二人の医師がデタラメにラベリングした場合に予想される一致率を求めていきます。先ほどと違い、完全一致した要素以外にも細かくみてく必要があります。尚これは2つのベクトルの直積をとることで簡単にできます。

$A医師の予測分布 \otimes B医師の予測分布 = (0.3, 0.3, 0.3) \otimes (0.3, 0.2, 0.5)$

0.09	0.06	0.15
0.09	0.06	0.15
0.12	0.08	0.2

さらに先述した重みですが、（3段階評価で）quadratic weigted kappaを採用した場合のweight tableは以下の様になります。

$w_{ij} = 1 - \dfrac{(c_i - c_j)^2}{2^2}$

0.0	0.25	1.0
0.25	0.0	0.25
1.0	0.25	0.0

後は、以下のような計算式で重みつけカッパ係数を算出することが可能となります。 $X$ が観察されたマトリックス、 $Y$ が先述したデタラメにラベリングした場合に予想される一致率です。

$k = 1 - \displaystyle{ \dfrac{ \sum_{i} \sum_{j} w_{i_j} X_{i_j} }{ \sum_{i} \sum_{j} w_{i_j} Y_{i_j} } }$

$X$ と $Y$ の要素積を全て合計した値となり $\kappa ≒ 0.66$ となります。

尚、あまり出てこない話題ですが補足すると、先述されたウェイトを以下の状態にして同じ計算をすると通常のカッパ係数が算出されます。

0.0	1.0	1.0
1.0	0.0	1.0
1.0	1.0	0.0

このことからも通常のカッパ係数と重み付けカッパ係数は本質的にあまり差がないことが分かります。

連関係数

　クロス集計表（名義尺度）における行要素と列要素の関連度合いを示す仕様として連関係数が存在します。

クラメールのV

　 $r$ 行、 $c$ 列のクロス集計表における行要素と列要素の関連の強さを示す指標で、 $\chi^2$ 統計量とサンプル数 $N$ を用いて次の様に定義される値です。クロス集計表における $\chi^2$ 統計量の算出方法については、かなり有名で多くの場所で目にすることも多いと思うのでここでは割愛しますが、行と列に関連性がなかった場合における期待値からのズレが大きいほどその値も大きくなる統計量のことです。

$V = \sqrt{ \dfrac{\chi^2}{N × min(r -1, c-1)} } (0 ≤ V ≤ 1)$

ユールのQ

　 $2$ 行 $× 2$ 行のクロス集計表における関連度の強さを示します。

例のようなクロス集計表の場合、以下の式で算出することができます。 $Q = \dfrac{ad - bc}{ad + bc}$

	Y1	Y2
X1	a	b
X2	c	d

リスク比とオッズ比

　こちらも頻出ですが、改めて見ていこうと思います。リスク比については、言葉を知っていなくても式を見れば大体どういうことなのか分かり易いと思います。逆にオッズ非はギャンブルの場面、もしくはロジスティック回帰などを学習する際に出てくることもあって言葉は知っててもその解釈はいまいちピンとこないというパターンも多い気がしています。以降、以下のマトリックスを例に説明していきます。なお一旦クリックありをイベントあり、クリックなしをイベントなしとしてみていきます。

	クリック(Y)
広告タイプ(X)	あり	なし	計
A	30	20	50
B	10	40	50
計	40	60	100

リスク比

　まず広告Aのリスク（クリックレート）は $30 / 50 = 0.6$ 、広告Bのリスクは $10 / 50 = 0.2$ になります。よってそのリスク差は $0.4$ 、リスク比は $0.6 / 0.2 = 3.0$ となります。

オッズ比

　まず広告Aのオッズは $30 / 20 = 1.5$ 、広告Bのオッズは $10 / 40 = 0.25$ となります。そのオッズ比は約 $1.5 / 0.25 = 6.0$ となります。

リスク比のメリット

　先ほどまでの例を見るとリスク比の場合、広告Aの方が広告Bよりも3倍CTRが高い！というような解釈が可能です。しかしながらオッズ比を引用して6倍効果がある！とはなりません。当たり前のように感じますが、意外にオッズが6倍！みたいな表現（多分競馬とかで耳にする？）をもとにその割合も6倍違うと勘違いしてしまうこともありそうな気もします。

オッズ比のメリット

　直感的な解釈に使用しづらいオッズ比ですが、では一体どういうメリットがあるのでしょうか？一つずつ見ていきましょう。

ケースコントロール研究（後ろ向き研究）

　先ほどは原因（広告タイプの違い）→ 結果（クリック）という流れで話を進めてきました。例えばA/Bテストなどはこのような形であらかじめ、実験群と統制群に分けた上で結果を後追いで観察していくことになります。しかしながら例えば、「この結果は原因Aによるものに違いない」という様な仮説を出発点として実験が行われる、あるいは肺がんと喫煙有無の関係性を調査したいが、そもそも肺がんを発症するのが稀である上に、長期間にわたって観察する必要があるなどの理由で、ケースコントロール研究が行われる機会は多く存在します。オッズ比はこのケースコントロール研究に対して、便利な性質が存在します。結論から先に話すと

ケースコンロール研究を行う場合においても、本当に知りたいのは、前向き研究（コホート研究）で得られるはずのリスク比
しかしケースコントロール研究ではコホート研究で得られるはずのリスクをうまく推定することができない
ただケースコントロール研究で得られるオッズ比からコホート研究で得られるオッズ比を推定することは可能

という便利な性質があります。つまりイメージとしては本来ものすごくCTR（クリックレート）が低いような状況下において、クリックした人100人とクリックしなかった人100人という全くの同数（現実には即さないような割合）でサンプリングしてしまった場合に計算される広告Aのリスク比は本来のものとかけ離れがちなのに対し、オッズ比はそう遠く離れないといった具合です。これはオッズ比が行・列どちらを起点に見ても値が変わらないという便利な性質が大きく関わっています。

　恣意的な例になりますが、以下の様なマトリックスを考えてみます。母集団は同じと仮定した上で、クリックした人としなかった人を同数集めています。

	クリック(Y)
広告タイプ(X)	あり	なし	計
A	45	20	64
B	15	40	55
計	60	60	120

　この様なデータから直接リスク比を求めることはできません。そもそも正確な比率でサンプルを取れていないためです。試しに無理やり計算してみるとわかると思います。

$(45 / 65) / (15 / 55) ≒ 2.58$ （先ほどと違う）

　同じ理屈でいくとオッズ比を求めることもできなそうです。理由としては、やはり正確な比率でサンプリングされていないからです。しかし、オッズの比の強みとして、行列を逆転させても同じ値が得られるという点です。試しに計算してみると

$(45 / 20) / (15 / 40) = 6.0$ （先ほどと一緒）

この性質がオッズ比の便利な点です。なお、証明は色々あるかと思いますが、ベイズの定理を使って以下のように示せます。

$\dfrac{ P(X=A | Y=1) / P(X=B | Y=1) }{ P(X=A | Y=0) / P(X=B | Y=0) } = \dfrac{ P(Y=1 | X=A) / P(Y=0 | X=A) }{ P(Y=1 | X=B) / P(Y=0 | X=B) }$

イベントを逆にしても（基本的には）同じ

　例えば今までの例と逆にクリックしなかった方を中心に見ていく場合、オッズの場合はその逆数を取るだけで値が一致するという数学的に便利な性質があります。これはリスク比にはない性質です。

ロジスティック回帰

　オッズは回帰モデルに応用しやすいという利点があります。例えば以下はロジスティック回帰の式ですが、下記のよう変更してくとオッズが現れることが分かります。

$p = \dfrac{ 1 }{ 1 + exp(-(a_{0} + a_{1}x_{1} + ... + a_{n}x_{n} )) }$

$1 - p = \dfrac{ exp(-( a_{0} + a_{1}x_{1} + ... + a_{n}x_{n} )) }{ 1 + exp(-( a_{0} + a_{1}x_{1} + ... + a_{n}x_{n} )) }$

$\dfrac{p}{1-p} = exp(a_{0} + a_{1}x_{1} + ... + a_{n}x_{n})$

左辺にオッズが出てきているのが分かります。ここで左辺と右辺を直線の関係にするために、両辺の対数を取り左辺をロジット関数に変換します。

$ln\dfrac{p}{1-p} = a_{0} + a_{1}x_{1} + ... + a_{n}x_{n}$

式を逆説的に辿りましたが、このようにロジスティック回帰とオッズは深く関連していることが分かります。

さてここで、仮に変数 $x_1$ が $0$ から $1$ に増えたとします。それ以外の $x_n$ は変わらないとすると。

$ln(x_{1} = 1 におけるオッズ) - ln(x_{1} = 0 におけるオッズ) = a_{1}$

$ln\dfrac{x_{1} = 1 におけるオッズ}{x_{1} = 0 におけるオッズ} \quad\quad = a_{1}$

$対数オッズ比 = a_1$

となることが分かり、ロジスティック回帰の回帰係数とオッズ比の関係性も見えてきます。

また、なぜ理解しやすいリスクではなくオッズを用いてるかという理由ですが、

$\dfrac{p}{1-p} = exp(a_{0} + a_{1}x_{1} + ... + a_{n}x_{n})$

の式の右辺の値域は無限に大きくなる値となっています。また左辺のオッズに関しても $p$ を $1$ に近づけるほど、無限に大きな値を取ることが分かります。この時仮に左辺にオッズではなくリスクを持ってこようとするとその値域が $1$ より大きな値を取れなくなってしまい都合が悪くなります。そこで、目的変数としてオッズを採用している訳です。

MIC

　相関係数と異なり、非線形の関係性も捉えようとして生み出された指標になります。

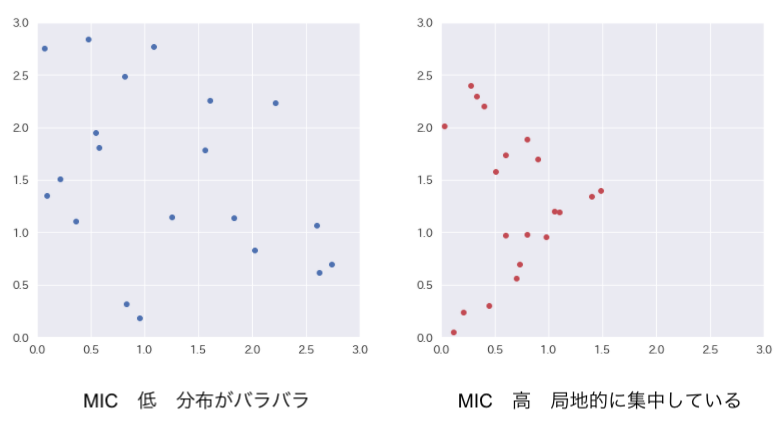
　上記のように局所的にデータの偏りが見られた場合、例えそれが非線形の関係性であってもMICは高くなる傾向があります。MICは今までの指標のような数式計算ではなくコンピューターを用いた計算が必要になります。計算方法ですが散布図の座標系に対し、相互情報量という数値が最大となるようなグリッドの区切り方を求め、その時の最大値を求めたのち $0$ - $1$ の範囲になるよう標準化した値になります。相互情報量は以下の式で定義されます。

$I(X, Y) = \sum_{x} \sum_{y} ln \dfrac{p(x, y)}{p(x) p(y)}$

この時 $p(x)$ と $[p(y)$ が独立であれば $p(x, y) = p(x) p(y)$ となり、相互情報量は $0$ となります。逆に両者が独立でない場合、 $x$ と $y$ の同時確率 $p(x, y)$ は積の法則より

$p(x, y) = p(y | x) p(x)$

となることからも $p(y)$ と $p(y | x)$ の差が大きい方が、相互情報量も大きくなることが分かります。

　次に例として以下の散布図に一つ線を引いた場合における相互情報量を求めてみます。

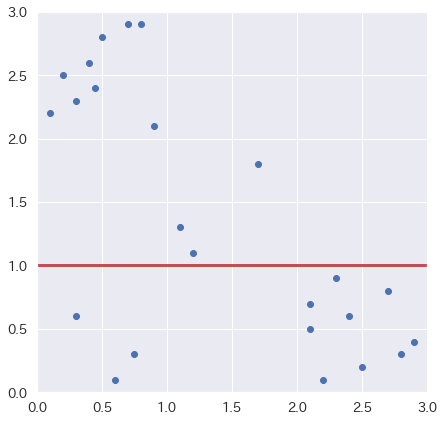
$\dfrac{1}{2} ln \dfrac{ \dfrac{1}{2} }{ 1 × \dfrac{1}{2} } + \dfrac{1}{2} ln \dfrac{ \dfrac{1}{2} }{ 1 × \dfrac{1}{2} } = 0$

分かりやすいですが、この場合線を引こうが引かまいが、グリッド毎の分布に差が出てないため、相互情報量は結局 $0$ となります。次に以下の様に線を追加してみます。

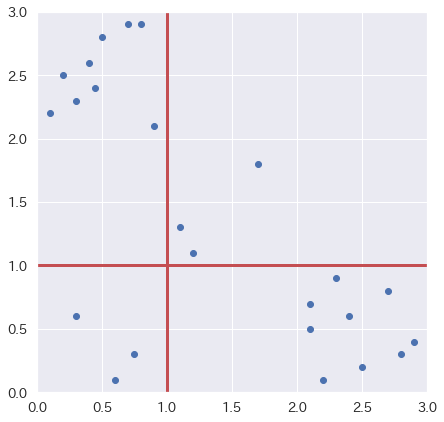
$\dfrac{3}{8} ln \dfrac{ \dfrac{3}{8} }{ \dfrac{1}{2} × \dfrac{1}{2} } + \dfrac{1}{8} ln \dfrac{ \dfrac{1}{8} }{ \dfrac{1}{2} × \dfrac{1}{2} } + \dfrac{3}{8} ln \dfrac{ \dfrac{3}{8} }{ \dfrac{1}{2} × \dfrac{1}{2} } + \dfrac{1}{8} ln \dfrac{ \dfrac{1}{8} }{ \dfrac{1}{2} × \dfrac{1}{2} } ≒ 1.52$

相互情報量が $+$ になったのが確認できると思います。尚、サンプル数を $N$ とした場合、 $N^{0.6}$ 本の線を引くことになっている様です。

MICのメリットとして、ピアソンの相関係数では算出できなかった非線形の関係をうまく表現できるところが挙げられます。逆にデメリットしては相互情報量を最大化させるために逐次線を決定していく必要があるため、どうしても計算量が増大してしまう点が挙げられます。

最後に

　最後に記事のまとめです。

ピアソンの積率相関係数の特徴とその注意点を意識して数字をみることが大切
ピアソンの積率相関係数に変わる様々な指標の特徴を理解した上で、ケースバイケースで使い分けることが大切

　株式会社ABEJAでは共に働く仲間を募集しています。興味ある方はぜひこちらの採用ページからエントリーください。

careers.abejainc.com

ABEJA Tech Blog

中の人の興味のある情報を発信していきます

実務で必須！２変数の関連性を正しく評価できるよう関連知識をまとめてみた