こんにちは、Research Internの荒尾(@karolis_ml)です。

日進月歩の勢いで研究が進んでいる深層学習ですが、教師あり学習でもっとも大事なデータのアノテーション、応用分野ではまだまだ大変ですよね。例えば、犬の写真から犬種を判断する分類器を作ろうとして教師データが必要になったとき、あなたは以下の画像にどんなラベルをつけるでしょうか?

f:id:karolis_ml:20190722105236j:plain — 出典: Pixabay

犬好きの方は正しくアラスカンマラミュート、そうではない方は似た有名犬種であるシベリアンハスキーと答えられたことでしょう。マラミュートの茶色い目(かわいい)や小さめの尖った耳(かわいい)を見分けて正しくラベル付けをするのは、決して簡単ではありません。

このようなアノテーションの分野に関して当ブログでは以前、Bounding BoxやSegmentationの効率化についての研究サーベイを行いましたが、この犬種分類のようなタスクでは、アノテーターのドメイン知識や作業自体の難しさによってラベルにノイズが出てきてしまいます。　 tech-blog.abeja.asia

そこで今回の記事では、ラベルにノイズが混在することを前提にしたとき、どのような手法で学習していくのかというテーマで、大まかな文献のレビューを行いたいと思います。最新の研究の紹介というよりは、先行研究に存在する様々なアプローチから代表的なものをそれぞれピックアップして紹介していくのが主な目的です。

また、重要な前提として、今回の記事でご紹介する多くのペーパーでは、ノイズが一様に分布しているという仮定のもと、CIFARやMNISTといったクリーンなデータに人工的にノイズを導入することによって、分類問題を解いてモデルのパフォーマンスを検証しています。この問題設定としては主に、全ラベルがある確率で違うクラスにアサインされるノイズ(Symmetric)と、各クラスごとにこの確率が変わるノイズ(Asymmetric)の二つがあります。

これらを踏まえて、以下の内容で分野やアプローチごとにペーパーを見ていきましょう。

統計的学習理論
深層学習におけるノイジーラベル
感想
References

統計的学習理論

実は深層学習の文脈でNoisy Labelsの研究が盛んになったのは最近のことで、2013年頃のこの分野の先駆者達は統計的学習理論を背景にしています。この分野からの論文を紹介する前に、まずは統計的学習の基礎であるEmpirical Risk Minimization (ERM)とProbably Approximately Correct (PAC) Learningについて簡単なおさらいをしておきます。

このおさらいの部分自体は以下の二つの論文のまとめを読む際にはなくても構わないので、読み飛ばしていただいても構いません。ただ、統計的学習理論では用語の使われ方やアプローチが違うので、機械学習からの橋渡し的にこれらのコンセプトを知っておくと少し論文自体が読みやすくなると思います。微分可能な損失関数を定義してパラメータを最適化していく機械学習的なアプローチに対して、これらの統計的機械学習理論ではよりフォーマルな問題設定がされている、と言うのが主なメッセージです。論文中では、ラベルにノイズがあるとき、学習の収束やモデルの汎化性能がどう変わるかの理論的な説明と証明がされています。

ERMとPAC Learnability

まず、あるサイズ$ m $のサンプルデータ$ S $と仮説$ h $(=機械学習でいうところの学習モデル)に対して、以下の経験的リスク(Empirical Risk)を定義します。

$R_{S}(h) \stackrel{\mathrm{def}}{=} \frac{\left|\left\{i \in[m] : h\left(x_{i}\right) \neq y_{i}\right\}\right|}{m}$

これは分類問題における単純な正答率(=Accuracy)と実質的には同じもので、0-1 Lossとも言われます。期待リスク(=True Risk)を計算するのは真のデータ分布が分からない状態では不可能なので、この経験リスクが最小になるような仮説$ \hat{h} \in H $を探すのがERMの目的です。

そして、あるデータ分布$ D $からサンプルされた$ S $について、この$ \hat{h} $による経験リスク$ R_{S \in D }(\hat{h}) $の上限が$ \epsilon $ ($0 \leq \epsilon \leq \frac{1}{2} $)によってバウンドされている場合、これを Approximately Correctと見なすことができます。さらに、この条件を満たす仮説がある一定の確率 $ 1 - \delta $ ($ 0 \leq \delta \leq \frac{1}{2}$)以上で学習できる場合、これをProbably Approximately Correct (PAC)と呼ぶことができます。

PACの重要な結果の一つが、学習に必要なサンプル数$ m $の下限を以下の式で上記の変数を使って表せることです。

$m \geq \frac{\log (|\mathcal{H}| / \delta)}{\epsilon}$

許容できるエラー率$ \epsilon $が下がったり、Approximately Correctな仮説を見つけられる確率$ 1- \delta$が上がる(つまり$ \delta $が下がる)と、必要なサンプルサイズが増加するのが分かると思います。$ |H| $は仮説スペースの大きさで、ここでは試行するアルゴリズムの数を意味します。この前提を元に、サンプルデータ$ S $に様々なラベルのノイズが加わった場合、Learnabilityとそのパラメータにどう影響があるのかを証明していくのが伝統的な統計的学習理論のアプローチになります(i.e. Angluin & Laird, 1988)。

ちなみに、ERMとリスクバウンドの一様性については、このチュートリアルのp.20辺りから詳しく触れられています。Rademacher Complexity等ここでは扱いきれない重要なコンセプトもカバーされているので、ぜひ参考にしてみてください。これらのコンセプトが根幹にあることを踏まえて、論文を見ていきましょう。

Learning from Noisy Labels (Natarajan et al., 2013)

Natarajan, N., Dhillon, I.S., Ravikumar, P.K. and Tewari, A., 2013. Learning with noisy labels. In Advances in neural information processing systems (pp. 1196-1204). https://www.cs.cmu.edu/~pradeepr/paperz/learning_nl_nips.pdf

統計的学習理論とノイジーなラベルの研究の中でもっとも重要なのが、NIPS 2013で発表されたこのNatarajan et al. (2013)です。当時は上に定義されたような0-1 Lossを元にした理論的結果がノイジーラベルの研究では主とされていたのですが、この損失関数自体は微分不可能であるため、計算的に損失関数の最適化をするためにはこれを近似するsurrogate loss functionが必要となります。SVMでいうとhinge loss、二値分類問題でよく使われるニューラルネットワークでいうと交差エントロピーなどがこれに当たります。

このペーパーでは、各クラスごとに異なった確率でランダムにラベルが変更されるノイズ(=Asymmetric Noise)に対して、これらの損失関数を修正する二つの一般化可能な手法(Unbiased Estimator, Label-Dependent Noise)が提案されています。

このうちより重要なのはLabel-Dependent Noiseで、この手法ではあらゆるsurrogate loss functionに対して、「ノイジーな分布$ D _ {\rho} $から学習した場合の損失の符号と、クリーンな分布$ D $から学習したベイズ分類器の符号が等しくなる」ような定数 $ \alpha $と損失関数$ \ell_{\alpha} $が存在することを示しています。つまり、あらゆるconvexなsurrogate loss function $ \ell $と予測値 $ t $、ラベル $ y $に対して、以下のような$ \alpha $によって重み付けされた損失関数を最小化することで、二値分類問題において最適な分類器を学習することができるのです(Theorem 11)。

$\ell_{\alpha}(t, y)=(1-\alpha) 1_{\{y=1\}} \ell(t)+\alpha 1_{\{y=-1\}} \ell(-t)$

この $ \alpha $はポジティブクラスのノイズ率$ \rho _ {+1} $(本来は正しく+1とラベルされているものが-1と間違ってラベルされている確率)とネガティブクラスのノイズ率$ \rho _ {-1} $の関数ですが(Theorem 9)、実際の実験ではこの定数 $ \alpha $は交差検証によって推定されています。

$\alpha^{*}=\frac{1-\rho _ {+1}+\rho _ {-1}}{2}$

このLabel-Dependent Noiseを使ったC-SVMによる実験結果が以下になります。ここでは人工的に生成された線形分離可能なデータセットにノイズを加えて学習させています。

クリーンな分布の(a)に対して、(b)と(c)ではノイズによってそれぞれのクラスの色が一部変わっているのが分かりますね。このノイズにも関わらず、これらの分類結果((b)と(c)がそれぞれ(d)と(e)に対応)では高い精度でこの二つのクラスの境界がクリーンな場合の境界に近い形で検出されています。

上で少し触れたように、この論文の大半はsurrogate functionを使った学習の収束についてのERMとPAC Learningのフレームワークでの証明に費やされて、主な貢献はそこから来ている印象です。少し残念なことに、応用でのこれらのパラメータの現実的な推定はそこまで考慮されていない印象で、上記の式の鍵であるノイズ率などに関してはフットノートで「このパラメータ実際にはわかんないよね〜」みたいなことが言われていました。つらい。~~せめて本文で言ってほしい。~~

Classification with Noisy Labels by Importance Reweighting (Liu & Tao, 2015)

Liu, T. and Tao, D., 2015. Classification with Noisy Labels by Importance Reweighting. IEEE Transactions on pattern analysis and machine intelligence, 38(3), pp.447-461. https://arxiv.org/abs/1411.7718

上記のNatarajan et al. (2013)を始めとする多くの研究では、surrogate loss functionにおけるノイズ率のパラメータ$ \rho $について、それが事前に分かっているもしくは交差検証によって推定することができるという仮定を置いていました。しかし、現実にはこの$ \rho $を推定するのは難しく、応用においては汎化性能や安定性に欠けるというのがこのLiu & Tao (2015)の出発点です。この問題を回避するために、著者らは上記の$ \rho _ {+1} $ と $ \rho _ {-1} $がそれぞれノイジーなラベルの$ P(+1|X) $ と $ P(-1|X) $によって上限でバウンドされることを示し、そしていかにノイジーなラベルによってもたらされる不確実性を推定して損失関数にウェイトをつけるかの手法を提案しています。

Gretton et al. (2009)によれば、ノイズの含まれたラベル$ \hat{Y} $とノイジーなデータ分布$ D _ {\rho} = (X, \hat{Y}) $から統計的学習をする場合、損失関数$ \ell(f(X), \hat{Y}) $に以下の項$ \beta $をかけることで、クリーンな分布$ D $に対しての期待リスクの最小化を図ることができます。また、ノイズは$ Y $にのみ掛かっているため$ P_D(X) = P_{D _ {\rho}}(X)$なので、

$\begin{aligned} \beta(X, \hat{Y}) &=\frac{P_{D}(X, Y)}{P_{D_{\rho}}(X, \hat{Y})}=\frac{P_{D}(Y | X) P_{D}(X)}{P_{D_{\rho}}(\hat{Y} | X) P_{D_{\rho}}(X)} \\ &=\frac{P_{D}(Y | X)}{P_{D_{\rho}}(\hat{Y} | X)} \end{aligned}$

とすることができ、これはノイズ率を用いて、

$\begin{aligned} \beta(X, \hat{Y}) &=\frac{P_{D}(Y | X)}{P_{D_{\rho}}(\hat{Y} | X)} \\ &=\frac{P_{D_{\rho}}(\hat{Y} | X)-\rho_{\hat{Y}}}{\left(1-\rho_{+1}-\rho_{-1}\right) P_{D_{\rho}}(\hat{Y} | X)} \end{aligned}$

とノイズを含む項のみで表すことができます(この式変形について詳しくは論文のSection 7.1を参照)。この中の$ P _ {D _ {\rho}} (\hat{Y} | X) $を推定する現実的な方法として、必要とされるデータ数が多く高次元では難しいとされているKernel Density Estimationの代わりに、Density Ratio Estimation Methodが提案されています。この方法では、Bregman DivergenceというConvexかつ微分可能な関数のためのダイバージェンスを使用することで、最適なDensity Ratioの近似を保証しています。Bregman Divergenceの統計的学習について詳しくはNock & Nielsen (2009)を参照してください。また、ノイズ率$ \rho _ {\hat{Y}}$については、先述の上限バウンドを元に、

$\rho _ {\hat{Y}} = \min _{X \in \mathcal{X}} P_{D_{\rho}}(\hat{Y} | X)$

によって推定をしています。

これらを元に、実験結果を見てみましょう。ベースライン手法は、上にご紹介したNatarajan et al. (2013)の二つの手法が採用されており、同じく線形分離可能な人工的データにノイズを加えてパフォーマンスを測る形になっています。UB$ \ell $はNatarajan et al. (2013)の一つ目の手法であるUnbiased Estimator、LD$ \ell $はLabel-Dependent Costの略で、このペーパーのImportance WeightingはIW$ \ell $で表されています。ノイズ率を高くするに従って分類精度が落ちていますが、IW$ \ell $はベースラインをそれぞれのノイズ率で上回っていることがわかります。

f:id:karolis_ml:20190723154136p:plain

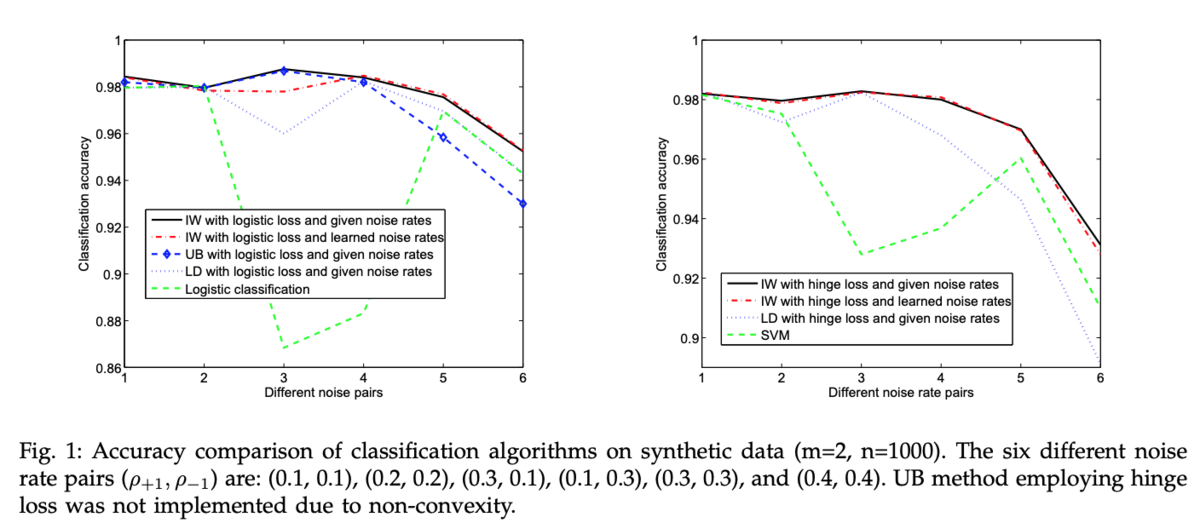
また、これらのノイズ率を推定した結果が以下のテーブルになります。Natarajan et al. (2013)が採用している交差検証による推定と比べて、著者らのDensity Ratio Esimation Methodのほうがより正確にノイズ率の推定をできていることが分かります。今回は省略していますが、UCIデータセットの心臓病や糖尿病等の分類タスクにおいても、Natarajan et al. (2013)と比べてより高い精度でノイズ率を推定できています。

f:id:karolis_ml:20190723155840p:plain

統計的学習理論の分野からはこの二本だけのエントリーに留めましたが、この分野では他にもノイズのProbabilistic Modellingなどにおいて貢献が多くあります。ただ全体的に、これらの手法はノイズ率の推定やパラメータの決定が不安定で、現代的な深層学習への応用は難しいイメージでした。新たなコンセプトを定義して実験セクションで既存手法に対してのパフォーマンスで勝負するような論文が多くなってきた機械学習に比べて、これらの統計的学習理論のペーパーでは学習の収束性やバウンド、汎化性能等についての証明が肝となっている場合がほとんどであるという印象を査読コメント等を読んでいて感じました。ただ、それを踏まえても、これらを理解することは学習におけるノイズ自体について考える際に有用であると思うので、ぜひこの分野からも論文を手に取ってみてください。

深層学習におけるノイジーラベル

このブログでもよく扱われているComputer Vision等のタスクで高いパフォーマンスを発揮している深層ニューラルネットワークですが、その構造や仕組みについては未だに完全に明らかにはなっていません。その一つとして、ネットワークが実際にデータに存在するパターンを学習している(Learning)のか、もしくは単に記憶しているだけ(Memorization)なのかという問題があります。

*このGeneralization vs Memorization問題については、Chatterjee (2018)が具体例と共にわかりやすく説明しています。

また、Arpit et al. (2017)は、DNNsは単にデータを記憶することも可能ではあるものの、先にシンプルなパターンをデータから学ぶ傾向があるとの実験結果を報告しています。これらの傾向を考慮すると、ノイジーなラベルはモデルの汎化性能に大きな負の影響を与えることになってしまいます。このセクションでは、ディープラーニングにおいてノイジーなラベルからいかに汎化性能の高いネットワークを学習させるかに焦点をおいて、三つの大まかなカテゴリに分けてご紹介していきます。

複数のネットワークを訓練するアプローチ

このアプローチでは、インプットデータの特性から学習しやすいサンプルとノイズの可能性の高いサンプルを分けて、ミニバッチ毎に複数ネットワークのパラメータを更新していきます。このセクションで扱う3本のペーパーを図解で表した分かりやすい図がCo-Teaching手法の提案者であるHan et al. (2018)の論文にあったのでまずこちらをご覧ください。赤と青で示されるフローは、ノイズによってバイアスのかかったエラーがどのように次のネットワークに伝播していくかを示しています。この図を頭に浮かべながら、具体的にそれぞれのペーパーを見ていきましょう。

f:id:karolis_ml:20190724172909p:plain — エラーの伝播フロー (Han et al., 2018)

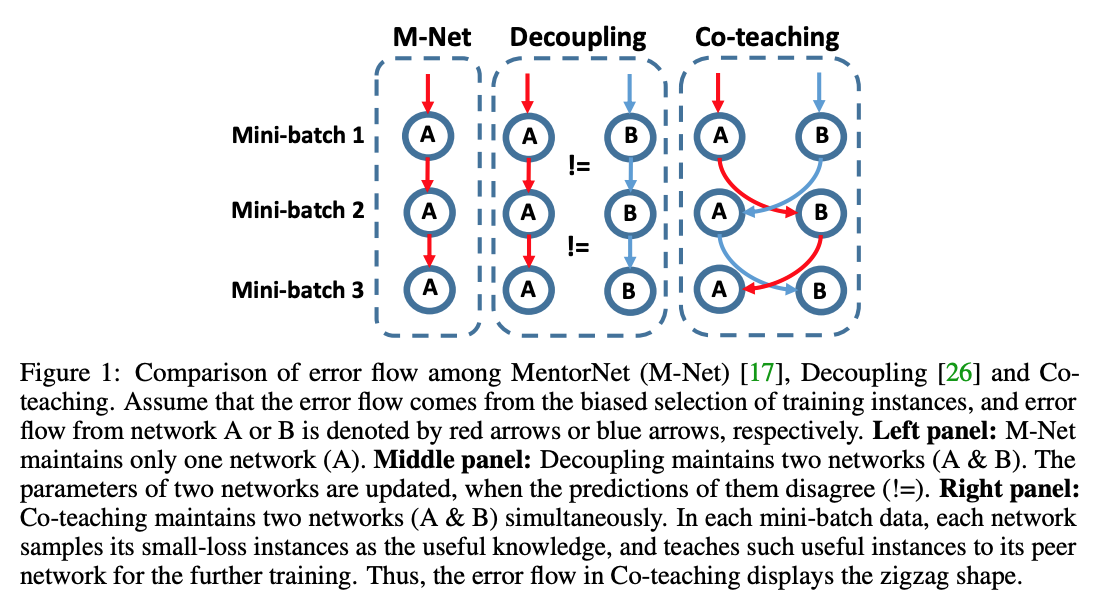
MentorNet (Jiang et al., 2017)

Jiang, L., Zhou, Z., Leung, T., Li, L.J. and Fei-Fei, L., 2017. Mentornet: Learning data-driven curriculum for very deep neural networks on corrupted labels. arXiv preprint arXiv:1712.05055. https://arxiv.org/abs/1712.05055

ICML 2018でも発表されたMentorNetは、かのBengio先生が2009年に同じくICMLで発表したCurriculum Learning (Bengio, 2009)にアイデアを得ています。このカリキュラム学習の要点は、学習をしていくタスクの難易度を段階的に上げていくことによって、より高い汎化性能を出すことができるというものです。Bengio (2009)では人工的に作ったデータセットを利用してShape DetectionとLanguage Modellingのタスクにおいてカリキュラム学習の有用性を示していましたが、カリキュラム自体のデザインが難しさが欠点とされていました。

このペーパーではこれを念頭に、StudentNetとMentorNetという二つのネットワークを使って、ミニバッチごとダイナミックにカリキュラム自体をデータから学習していく点を新規性としています。カリキュラムは以下の図におけるMentorNetによって学習され、これは各サンプルの重みづけとしてStudentNetの学習データに影響を及ぼしていきます。ここでは、Chang et al. (2017)にあるように、損失とその移動平均との差に対してLSTMを使うことによって予測値の分散を保持しています。損失を計算するという点では一つのネットワークなので上記のHan et al. (2018)の図では単一ネットワークに見えますが、この裏では各バッチごとにStudentNetとMentorNetによる訓練が行われています。 f:id:karolis_ml:20190727105539p:plain

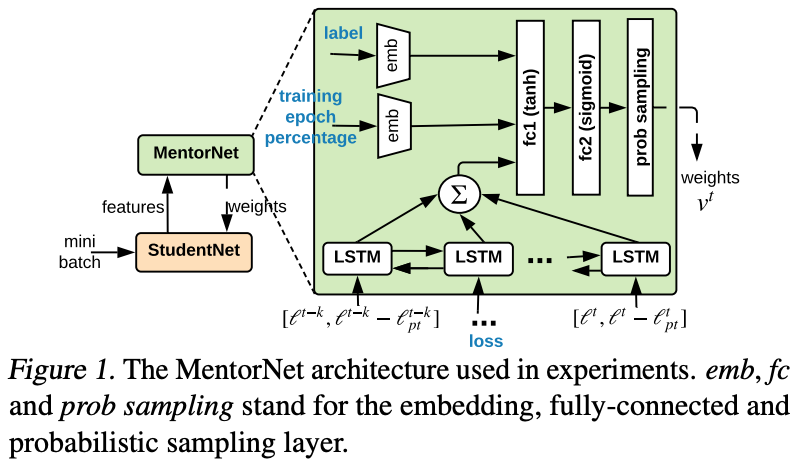
この次のセクションで紹介するReed et al. (2014)らのBootstrapping等と比べて、CIFAR-10/100でのノイズ率40%での実験ではより高い精度を達成しています。 f:id:karolis_ml:20190724184227p:plain

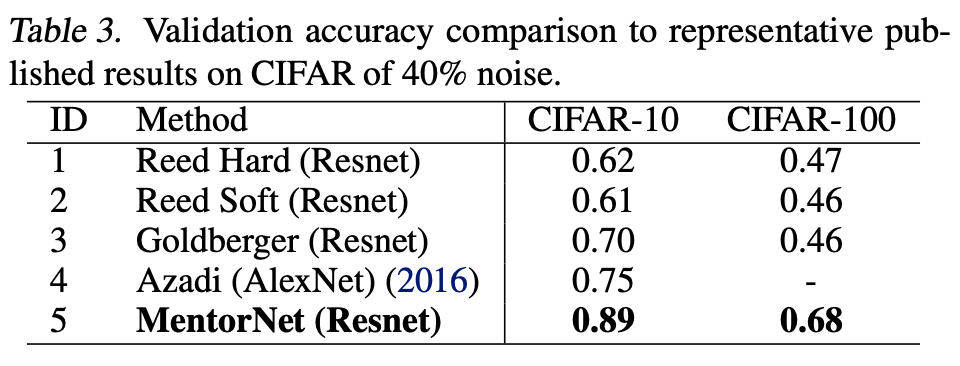
ここで特筆すべきなのは、エポックが進むに連れてカリキュラムの性質が変化していくという点です。以下の図では、$ z $軸に各サンプルに与えられている重み、$ x $軸に損失の移動平均の差( $ \ell_i - \lambda $ )、$ y $軸に( $ \ell_i $ )が表されており、初期のエポック(epoch=21)では、損失の大きいサンプルにより大きい重みが付けられているのに対して、学習後半のエポック(epoch=76)では、全体的にサンプルに関連つけられる重みが小さくなっています。

f:id:karolis_ml:20190724182511p:plain

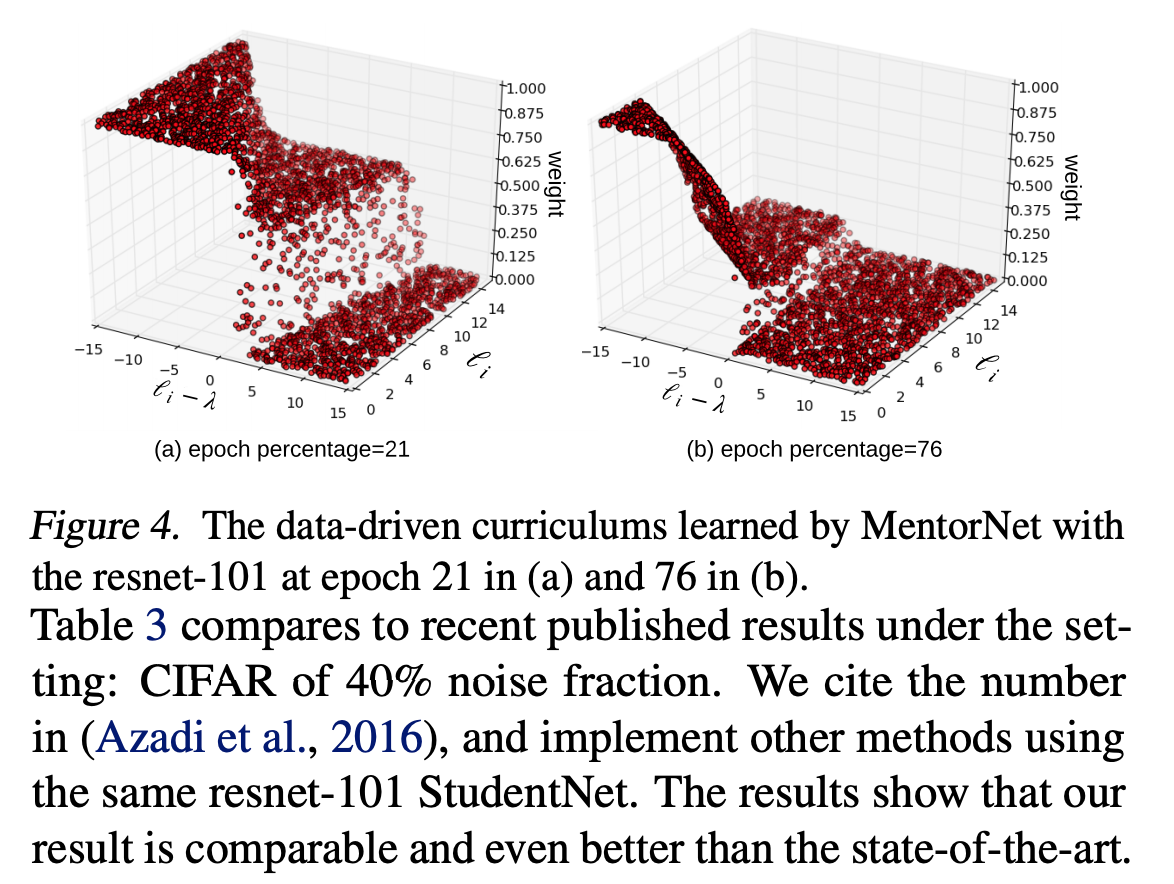
注意するべきポイントとしては、元来のカリキュラム学習の欠点にもあるように、サンプルの選択方法によってはカリキュラム前半で蓄積されたエラーが学習プロセス全体に蔓延してしまうという点です。2年前に別のインターン先でカリキュラム学習についての勉強会をBengioのペーパーを元にしたのですが、その当時に問題とされていたカリキュラム自体の学習をデータからできる点は画期的なように思えますね。

Decoupling (Malach & Shalev-Schwarz, 2017)

Malach, E. and Shalev-Shwartz, S., 2017. Decoupling" when to update" from" how to update". In Advances in Neural Information Processing Systems (pp. 960-970). https://papers.nips.cc/paper/6697-decoupling-when-to-update-from-how-to-update.pdf

NIPS 2017で発表されたヘブライ大学の研究者らの論文です。上記の図でも見たように、Decouplingはそれぞれのミニバッチにおけるあるサンプルに対して二つのベースとなる分類器が異なる予測をしたときのみ、それを新たなサンプルとしてネットワークの重みをそれぞれ更新する仕組みです。この二つのネットワークは、ランダムなウェイトでそれぞれ初期化をするよりも、訓練の初期の段階では損失関数をもとに重みを更新、訓練の後半では分類器の予測が一致するかどうかによって重みを更新することで、より高いパフォーマンスを得られることがこのペーパーでは経験的に示されています。この結果は、ネットワークが先にシンプルなパターンを学習してから複雑なパターンを記憶し始めてしまうという、Memorization Effectの研究結果に即しています。また、仮にラベルの信頼度の高いGround Truthと言えるデータがある場合、それをバリデーションセットとして使うことでより汎化性能の高いネットワークを選ぶことが提案されています。

f:id:karolis_ml:20190725154522p:plain

実験セクションでは、Labeled Faces in the Wild (LFW)という顔の画像に名前のラベルが付いているデータに対して、名前から性別を自動的に予測する外部のサービスを使うことによってノイジーなラベルを作り出しています。ここでは以下のような誤分類(男性の名前から女性と判断された例)がみられ、KimやJoanのような言語によって性別が違う名前、Morganのような中性的な名前などがノイズの原因になっているようです。ここで生成されたノイジーな性別のラベルを$ Y $、元の画像を$ X $として学習を行うのが今回の実験の中身です。

f:id:karolis_ml:20190725150104p:plain

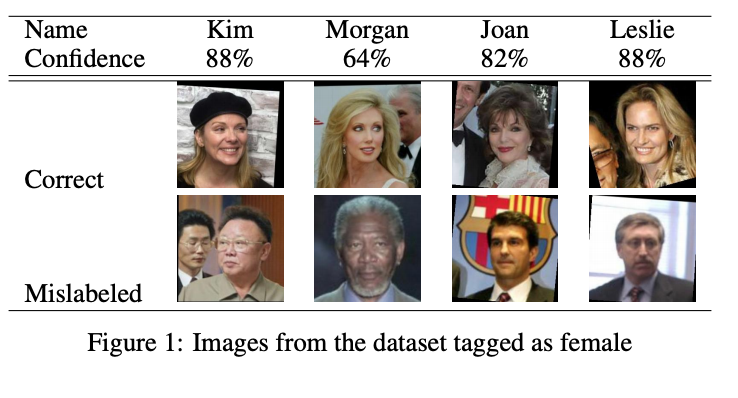
ここから、名前から性別を与えるサービスのConfidenceを利用して、100％の信頼度で予測された名前、[90%, 100%)で予測された名前、[0%, 90%)で予測された名前にデータセットを分割して、 Decouplingを使ってミニバッチ毎にSGD Momentumで学習していった結果が以下のグラフになります。ノイズが多い場合と少ない場合共に、同じネットワーク構造で学習した一つのネットワークに比べて、高いパフォーマンスを発揮しているのが分かります。また、この実験とCo-Teachingの実験で登場するBootstrappingは、その先でご紹介するReed et al. (2014)による手法です。

f:id:karolis_ml:20190725152037p:plain

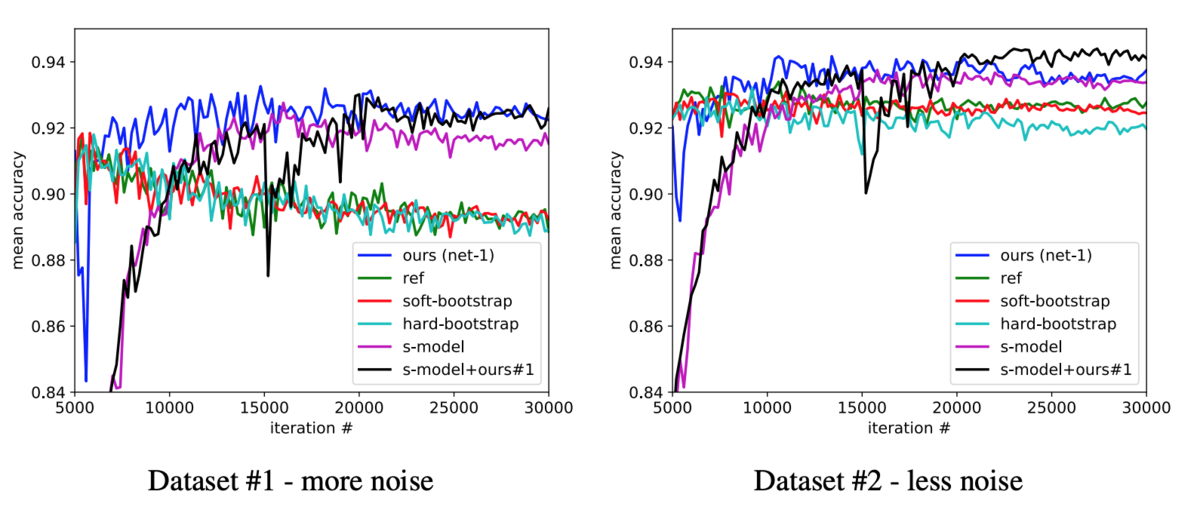
非常にシンプルなアプローチですが、この実験結果ではうまくワークしているのが分かります。ただ、このノイズが他社サービスのアルゴリズムによって作り出されている点は、ノイズ自体の分布などに関して少し気になるところです。また、このDecouplingが実際どれだけうまく行くのかについては疑問が残る点も多いです。モデル$ h_1 $と$ h_2 $の予測が一致しない場合にそのサンプルがノイジーな可能性が高いと考えると、これだけで訓練した場合は過学習に陥ってしまうような気がしないでもありません。

また、予測が一致したインプットがそのイテレーションでは学習されないという点も気になります。上記のグラフでは一見エポックが大きくてもMentorNetでは過学習を起こさないような印象を得ますが、これが予測の一致しないサンプル$ S $からうまく学習できた結果なのか、ミニバッチからサンプルを選ぶこと自体がDropout的な役割を果たしているからなのか、具体的な仕組みはよくわかりません。SVMの境界面の分類のようなイメージで考えると、細かいところでHyperplaneの前後を調整するようなイメージも湧くのですが、果たしてこれを二つで繰り返して行くことでうまく行くのかどうか、なかなかお気持ちが分かりかねるのが正直なところです。

また、この実験結果はNIPSのReviewer 1によると"very weak"とのことで、「こんな小さいジェンダー分類？のデータセットなんかで実験してSOTAとか言うな(意訳)」とのコメントがされています。この分野に関してはアノテーションにおけるノイズという応用MLにおいて非常にRelevantな問題だけに、多少現実的な問題設定がされていると興味をそそられるのですが、やはり手法の比較と言う面ではCIFAR10にランダムノイズ、とといった手法が好まれるような印象です。

Co-Teaching (Han et al., 2018)

Han, B., Yao, Q., Yu, X., Niu, G., Xu, M., Hu, W., Tsang, I. and Sugiyama, M., 2018. Co-teaching: Robust training of deep neural networks with extremely noisy labels. In Advances in neural information processing systems (pp. 8527-8537). http://papers.nips.cc/paper/8072-co-teaching-robust-training-of-deep-neural-networks-with-extremely-noisy-labels.pdf

同じくNIPS 2018で発表されたCo-Teachingは、二つのネットワークを同時にトレーニングするという点ではDecouplingと同じなのですが、ここではあるミニバッチから訓練されたサンプルの中でそれぞれ損失が小さくなるようなものを使って、もう片方のネットワークの重み調整に利用するという点でアプローチが違っています。この擬似コードは以下になります。

f:id:karolis_ml:20190725153837p:plain

このCo-Teachingの比喩として、論文中では学生がお互いの宿題をチェックし合うPeer-Reviewが例に出されています。自分の解答のミスを見つけるのはその解答に至った思考プロセス等の個人のバイアスがあって難しいが、友人の解答であればミスを発見するのが比較的簡単である、というものです。先ほどのDecouplingと比べると、あるネットワークで学習できなかった分をもう片方のネットワークに学習させるというのは、バイアスを修正するという意味では納得が行くような気がします。

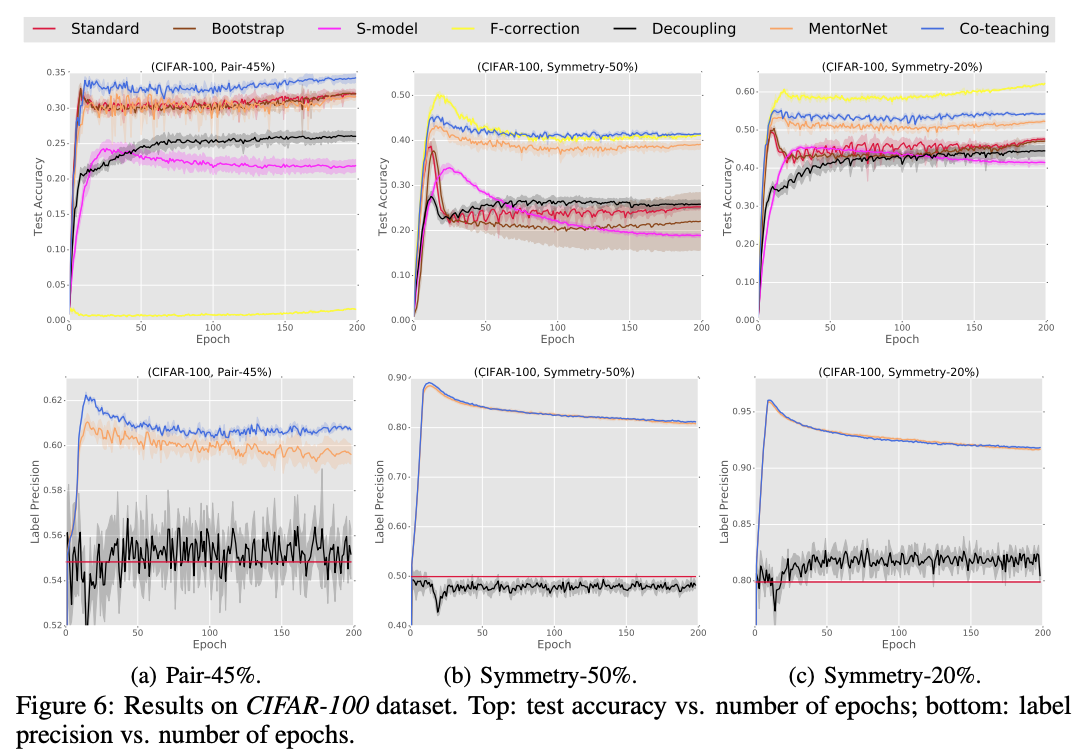
同じネットワーク構造を使ったCIFAR-10とCIFAR-100の結果がこちら。高いノイズレベルでの学習において特に高い精度を出していることがわかると思います。このあとのセクションの一部でご紹介するデータの一貫性を正規化項として損失関数に追加するアプローチは、これらの複数ネットワークのトレーニングをする手法と一緒に適用することが可能です。

f:id:karolis_ml:20190725155747p:plain

f:id:karolis_ml:20190725155839p:plain

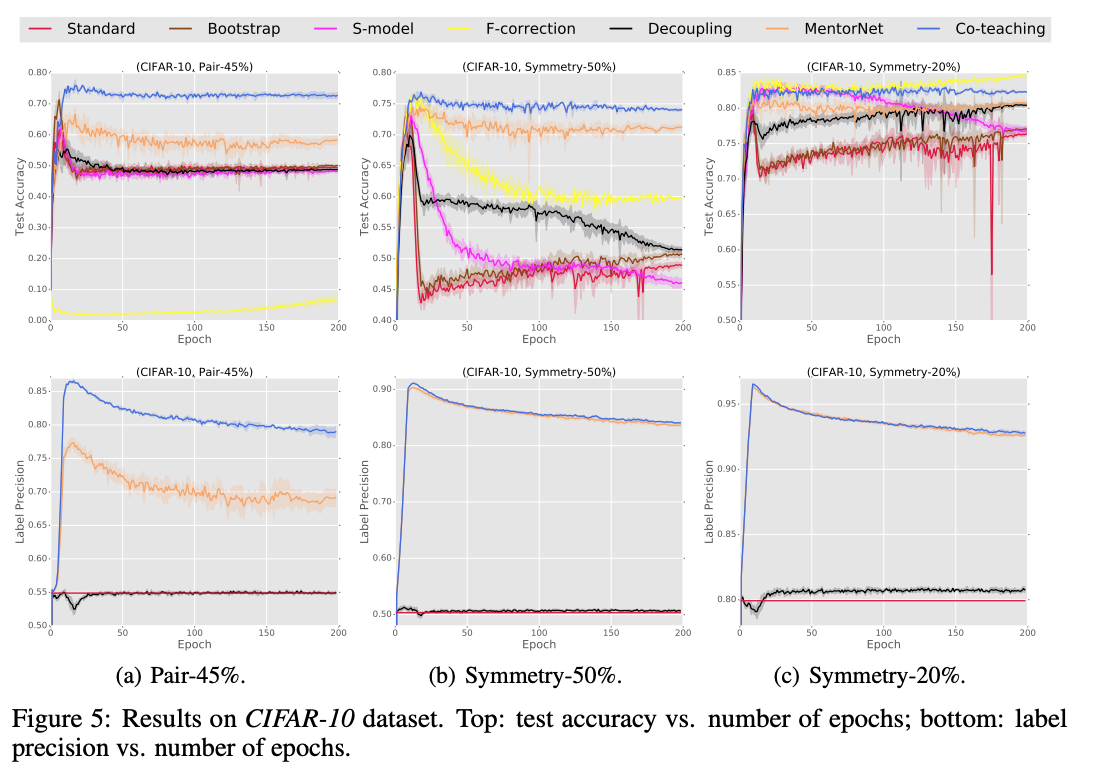
データの一貫性をSemi-Supervisedに学習するアプローチ

Training Deep Neural Networks on Noisy Labels with Bootstrapping (Reed et al., 2014)

Reed, S., Lee, H., Anguelov, D., Szegedy, C., Erhan, D. and Rabinovich, A., 2014. Training deep neural networks on noisy labels with bootstrapping. arXiv preprint arXiv:1412.659. https://arxiv.org/abs/1412.6596

統計的学習理論がSVMやロジスティック回帰を実験で使っていたのに対して、ICLR 2015で発表されたこの論文は、深層ニューラルネットを前提としたノイジーラベルでの分類問題での学習にフォーカスを当てた、よりモダンなアプローチになります。

DNNにおいてはDropoutに過学習を防ぐ効果があることは知られていますが、主観的なラベル付けや不完全なラベルに対応することができません。そこで、予測の一貫性をインプットの類似性から考慮してトレーニングのObjectiveに組み込むことで、ノイズの入ったデータを直接学習しないような工夫がされています。つまり、ネットワークの学習した特徴量において、似たインプットは似たアウトプットを伴うべき、というのが根幹のアイデアです。具体的には、訓練データをミニバッチSGDで処理する過程で、現在のモデルのアウトプット(i.e. 確率ベクトル)を元にターゲットのラベルを更新していくことによって、より高いconfidenceで予測がされるような損失関数を作ることでこれを達成しています。

ここでは、この後に書かれたペーパー等でも頻繁に比較対象とされるBootstrappingをご紹介します。ターゲットベクトルを$ \textbf{t} $、ネットワークのアウトプットを確率ベクトル$ \textbf{q} $とすると、マルチクラスでの交差エントロピーは通常であれば$ -\sum _ {k=1}^{L} t_k \log \left(q_k\right) $と定義されます。それをここでは、ハイパーパラメタ$ \beta $と共に以下のように定義して損失関数に組み込むことによって、アウトプットの確率分布自体をSGDの最適化対象の一部としています。

$\mathcal{L} _ {s o f t}(\mathbf{q}, \mathbf{t}) = \sum _ {k=1} ^ {L} \left[\beta t _ {k}+(1-\beta) q_{k}\right] \log \left(q_{k}\right)$

この確率分布を損失関数の一部として学習するアプローチは、NIPSで発表されたGrandvalet & Bengio (2005)のMinimized Entropy Regularizationと類似していて、こちらのペーパーでは半教師あり学習の文脈においてラベル付けのされていないデータにラベルをつける際に同じくネットワークのアウトプットが使われています。

また、$ \mathcal{L} _ {s o f t} $がネットワークのアウトプット$ \textbf{q} $を直接使っているのに対して、$ \mathcal{L} _ {h a r d} $ではこれをMAP推定に通したベクトル$ z _ {k} :=\mathbb{1}\left[k=\operatorname{argmax} q _ {i}, i=1 \ldots L\right]$を$ q_i $の代わりに使っています。

さらに一般的には、このSoftとHardの中間的なアプローチも可能ですが、以下の実験ではSoftとHardのみがそれぞれ使われています。ここでは、MNISTに加えて以下のToronto Faces Database Emotion Recognitionというタスクで実験が行われています。ここでは人工的なノイズの注入はせず、本来のラベル自体の一貫性があまりない、表情からの7つの感情の分類問題を解いています。ここではsoftmaxのベースラインをBootstrap HardとReconstructionが上回る結果となりました。Reconstructionはデータ分布への仮定がここでご紹介したものより少し厳しいBootstrap法です。詳しくはペーパーをご参照ください。 f:id:karolis_ml:20190726145730p:plain

Joint optimization framework for learning with noisy labels (Tanaka et al., 2018)

Tanaka, D., Ikami, D., Yamasaki, T. and Aizawa, K., 2018. Joint optimization framework for learning with noisy labels. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (pp. 5552-5560). https://arxiv.org/abs/1803.11364

Reed et al. (2014)に続いてこちらもネットワークのパラメータ$ \theta $とラベル$ y $の学習を同時に行うアプローチになります。 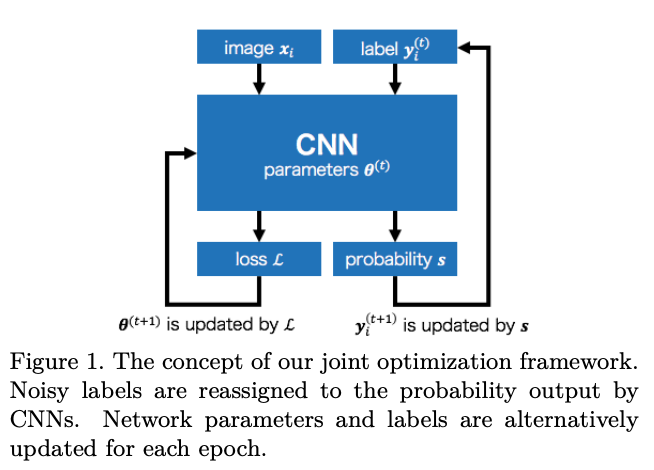f:id:karolis_ml:20190724155134p:plain 学習するラベルはもっとも高い確率のクラスが1を取るOne-Hotベクトルで表されるHardラベルと、確率ベクトルをそのまま使うSoftラベルに分けられます。そして、ネットワークの確率モデルを$ \textbf{s} $としたとき、モデルのアウトプットと実際のラベルの分布の間の損失は以下のようにKL Divergenceを使って求めます。

$\mathcal{L}_{c}(\boldsymbol{\theta}, Y | X)=\frac{1}{n} \sum_{i=1}^{n} D_{K L}\left(\boldsymbol{y}_{i} \| \boldsymbol{s}\left(\boldsymbol{\theta}, \boldsymbol{x}_{i}\right)\right)$

このペーパーの新規性は、ネットワークのパラメータ$ \theta $とラベル$ Y_i $の片方を固定しながら、SGDによって$ \mathcal{L}_{c} $ともう片方を最適化していく点にあります。このようにAlternatingに最適化をする際に重要な正規化項が以下の二つです。

まず第一に、あるモデルのパラメータ$ \theta $を固定してラベル$ Y_i $を調整するとき、これをこのまま$ \mathcal{L} _ {c} $の最小化だけを基準に学習してしまうと、全てのインプット$ X_i $に対してある一定のクラスだけを返すようなtrivialな解に辿りついてしまいます。これを防ぐために、クラスの事前分布$ \overline{\boldsymbol{s}}(\boldsymbol{\theta}, X) $をミニバッチから近似して、その分布との差をKL Divergenceを取って正規化項$ \mathcal{L}_{p} $とすることで、修正された新たなラベルがこの事前分布と近くなるようにしています。ただし、クラスの数があまりにも多い場合や著しくデータが不均衡な場合は、このアプローチは適切とは言えません。

$\mathcal{L}_{p}=\sum_{j=1}^{c} p_{j} \log \frac{p_{j}}{\overline{s}_{j}(\boldsymbol{\theta}, X)}$

第二に、softラベルにおいて、確率が多クラスに分散して局所解に陥るのを防ぐために、以下のエントロピー損失を追加することで一つのクラスに確率が集中するようにします。

$\mathcal{L}_{e}=-\frac{1}{n} \sum_{i=1}^{n} \sum_{j=1}^{c} s_{j}\left(\boldsymbol{\theta}, \boldsymbol{x}_{i}\right) \log s_{j}\left(\boldsymbol{\theta}, \boldsymbol{x}_{i}\right)$

これらの正規化項はハイパーパラメータ$ \alpha, \beta$をそれぞれ伴って損失として最適化されます。

実験結果はCIFAR10にSymmetric NoiseとAsymmetric Noiseを加えたもので、以下のテーブルではAsymmetricなノイズのときの他の手法との比較をしています。ここでもまた高い精度でクリーンなデータでのAccuracyに追従した結果が出ていることが分かります。 f:id:karolis_ml:20190726111606p:plain

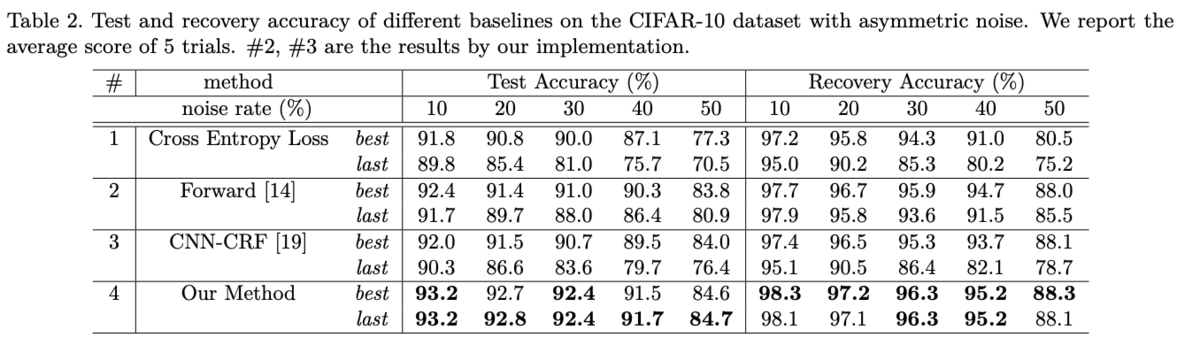
また、Generalization vs Memorizationについての考察が、Symmetric Noiseを加えたCIFAR10の実験結果からなされています。ここでは、学習率(learning rate)を変えてそれぞれ学習をすることで、低い学習率の場合を使ったときに学習プロセスの後半(エポックが大きいとき)にモデルがノイズにOverfitしてしまっていることを示しています。綺麗なデータセットに慣れているとやってしまいがちですが、ラベルのノイズや不一致について考えずに低いlearning rateで学習を回さないようにしましょう。 f:id:karolis_ml:20190725184853p:plain

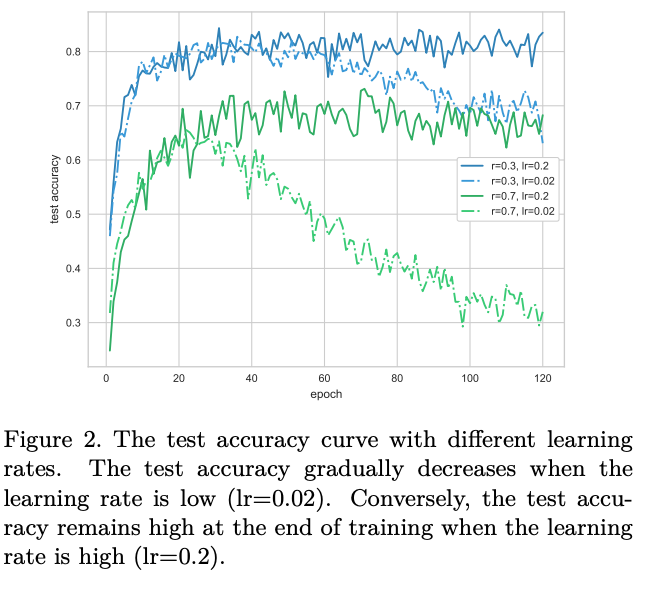
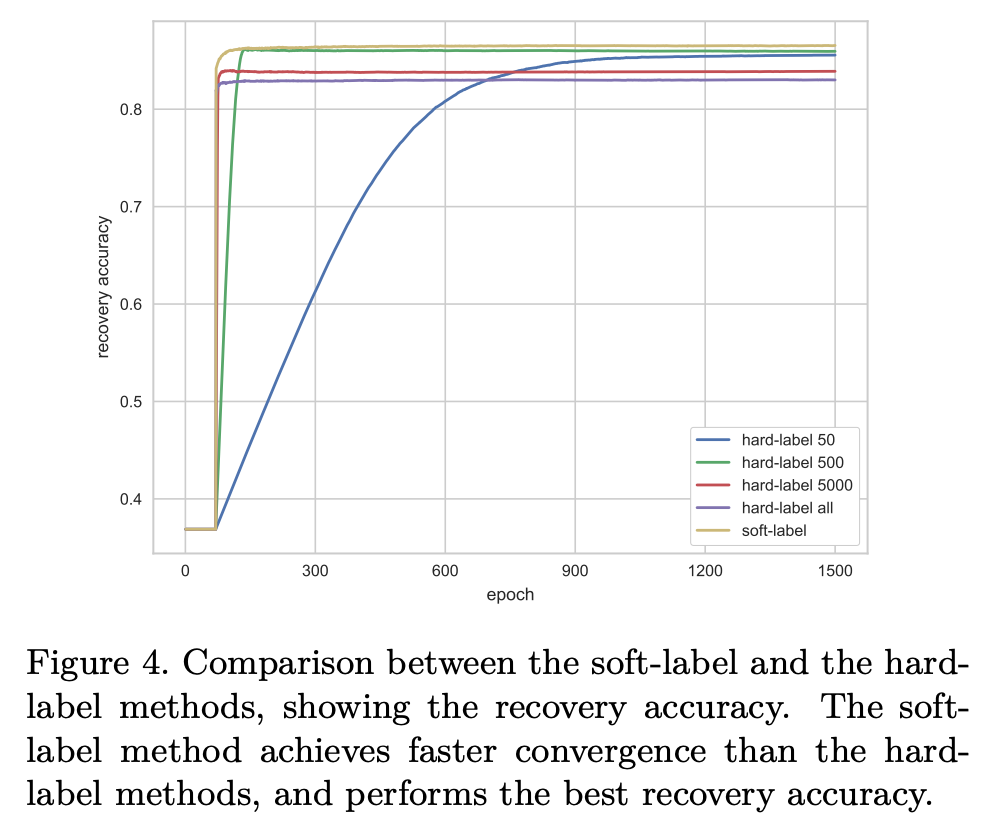
上述のHardラベルとSoftラベルについての違いは、以下の図が示すようにSoftラベルのより速い学習の収束と高い回復率(再アサインされたラベルの精度)が示されています。筆者らは、Softラベルに含まれる確率的なモデルの確信度が、学習において有用な情報となると考察しています。また、Distillationという、小さくクリーンなデータから学習したモデルを使ってノイジーなデータの学習を助ける手法を提案したLi et al. (2017)も、この確率的なモデルの確信度を"soft target"として使うことが有効であるとの考察をしています。

f:id:karolis_ml:20190726112922p:plain

Temporal Ensemble (Laine & Alia, 2017) / Mean Teacher (Tarvainen & Valpola, 2017)

Laine, S. and Aila, T., 2016. Temporal ensembling for semi-supervised learning. arXiv preprint arXiv:1610.02242. https://arxiv.org/abs/1610.02242

Tarvainen, A. and Valpola, H., 2017. Mean teachers are better role models: Weight-averaged consistency targets improve semi-supervised deep learning results. In Advances in neural information processing systems (pp. 1195-1204). https://arxiv.org/abs/1703.01780

この二つの論文は以前このブログでも紹介されていましたが、これらの手法は「インプットの特徴量を元にラベルの一貫性を学習する」といった点で上記のReed et al. (2014)とアプローチは近いです。ここで重要なのは、DropoutやData Augmentationといった確率的にもたらされる揺らぎを制限しようとしている点です。

簡単におさらいをすると、Temporal Ensemblingでは、インプット$ x $、ラベル$ y $、確率的な揺らぎを表す確率変数$ w $による識別モデル$ P(y|x, w) $において、以下を正規化項として損失関数に追加することでモデルの一貫性を保っていました。

$\sum _ {y}\left(p\left(y | x _ {i}, w _ {i}\right)-\overline{p}\left(y | x _{i}\right)\right)^{2}$

ここでいう$ \overline{p} (y | x _ {i}) $は、過去のイテレーションにおける移動平均です。これに対してMean Teacherでは、モデルパラメータの移動平均$ \overline{\theta} $を用いたモデルの出力と一致するように学習をしていきます。

$\sum_{y}\left(p\left(y | x_{i}, w_{i} ; \theta\right)-p\left(y | x_{i}, w_{i}^{\prime} ; \overline{\theta}\right)\right)^{2}$

これらの手法とTemporal Ensembleを修正した追加実験については、以下の記事を参照してください。 tech-blog.abeja.asia

また、これらのSemi-Supervisedな手法において考慮するべき点の一つに、実験の再現性と(不)公平な比較実験環境があります。上記ブログの追加実験をされたABEJA Researcherの白川さんが以下のように書かれているように、一部のペーパーの実験のセクションの評価は疑問の残る部分もいくつかあるのが実情です。

なお、たとえばMean Teacherのオリジナル実装はshake shake regularizationを使っていたりデータセットに合わせたパラメータチューニングがかなりされていたり、手法の比較としてどうなのかなと思うところはあったりなかったり。。。それらのチューニングを入れないで実装すると、オリジナル実装ほどの精度は出にくいです。このあたりについては、最近、半教師あり手法の評価について再考すべしという論文[9]がでて、同じことを感じていたのは自分たちだけではなかったのだと、ちょっと安心しました（しかも著者にI. Goodfellowもいるし）。精度競争の弊害なんでしょうか。

これはすごく大事なポイントで、半教師あり学習については初期値やランダムに注入されるノイズの性質、また、学習段階の初期においての損失など、学習結果を大きく左右しかねない問題が数多くあります。またこの記事で言及されているように、これらの評価方法の問題点についてはOliver et al., (2018)等で詳しくまとめられています。

Paired Softmax Divergence Regularization (Chen et al., 2019)

Chen, P., Liao, B., Chen, G. and Zhang, S., 2019. A Meta Approach to Defend Noisy Labels by the Manifold Regularizer PSDR. arXiv preprint arXiv:1906.05509. https://arxiv.org/abs/1906.05509

こちらの論文も上記の二手法と似たアプローチを採用しています。Softmax関数のアウトプットが確率ベクトルであることを利用して、Data Augmentationによってある$ x $から生成されたインプットのペア$x', x"$のネットワークにおける違いをKL Divergenceを取って正規化項としています。つまり、近隣のデータのペアは、それぞれ確率分布的には近くあるべきだというのがこの手法の根拠です。この正規化項はPaired Softmax Divergence Regularization (以降PSDR)と呼ばれます。

$\mathcal{L}_{P S D R}(x ; \theta)=\sum_{t} K L\left(f\left(x_{t}^{\prime} ; \theta\right) \| f\left(x_{t}^{\prime \prime} ; \theta\right)\right)$

Chen et al. (2019)はこの手法の高いパフォーマンスについてのディスカッションで、ラベルのないデータからも情報を得ることができる点に言及しています。これはTemporal EnsembleやMean Teacherにも当てはまります。

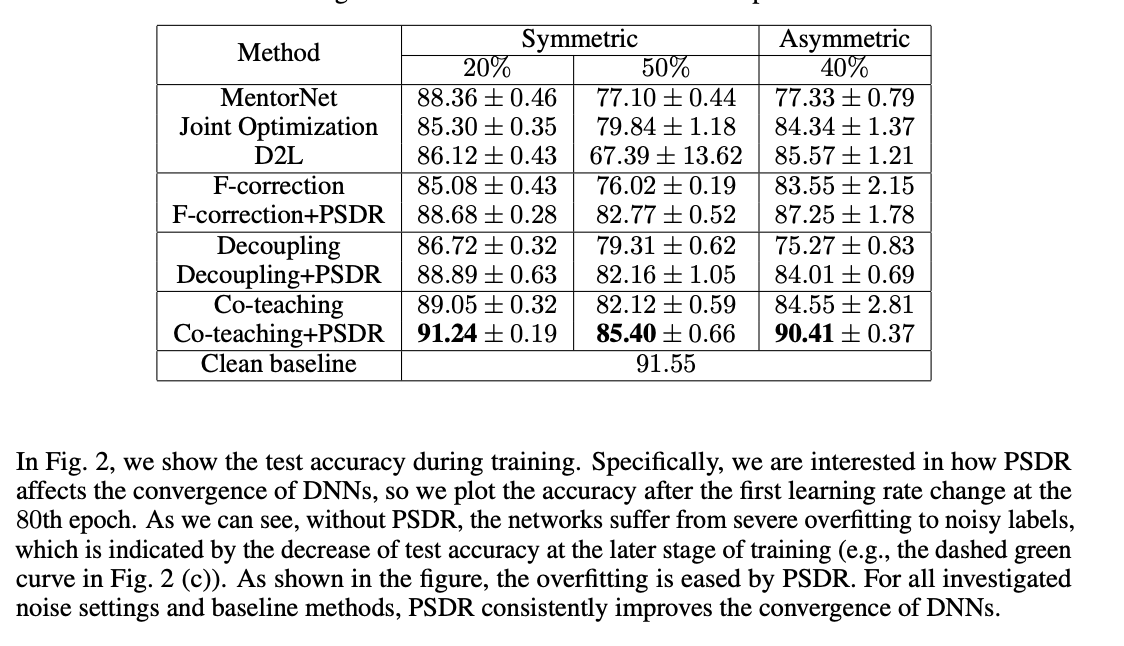
これらを元に、このペーパーでは上記の「複数ネットワークをトレーニングするアプローチ」で紹介したCo-TeachingやJoint Optimization等の手法にPSDRの正規化項を加えて実験を行なっています。実験ではCIFAR-10に人工的にラベルにノイズを加えたものがResNetで訓練されています。Test Accuracyの上昇はLearning rateの変化によるもので、Co-Teaching + PSDRが最も高いパフォーマンスを発揮しています。

f:id:karolis_ml:20190725180036p:plain

また、クリーンなデータでのベースライン精度91.55に対して、Symmetric(20%, 50%)とAsymmetric(40%)なノイズに対してそれぞれ91.24% ± 0.19, 85.40% ± 0.66, 90.41% ± 0.37と、高い回復率で他のモデルを上回る学習結果となっています。これまでの先行研究と比べてインプットの一貫性をKL Divergenceで測るというのはそこまで画期的な手法にも見えないように感じますが、ここではSOTAとなっているようです。

f:id:karolis_ml:20190725180808p:plain

複数のアノテーターの特徴を学習するアプローチ

Regularized Estimation of Annotator Confusion (Tanno et al., 2019)

Tanno, R., Saeedi, A., Sankaranarayanan, S., Alexander, D.C. and Silberman, N., 2019. Learning From Noisy Labels By Regularized Estimation Of Annotator Confusion. arXiv preprint arXiv:1902.03680. https://arxiv.org/abs/1902.03680

ここでは少し趣向を変えて、アノテーターの特性を学習することでノイジーなラベルから真の分布を見出すアプローチをご紹介します。

CVPR 2019でも発表されたこのペーパーで重要なのは、複数いるアノテーターのそれぞれのスキルや特徴をConfusion Matrix (CM)として推定する点です。分類モデルによるラベルの確率的分布とこのCMの積を取ってそれらのノイジーなラベルとの交差エントロピーを最適化することで、それぞれのCMとモデルパラメータを同時に学習していきます。このスキームは以下に図解されています。

f:id:karolis_ml:20190725161557p:plain

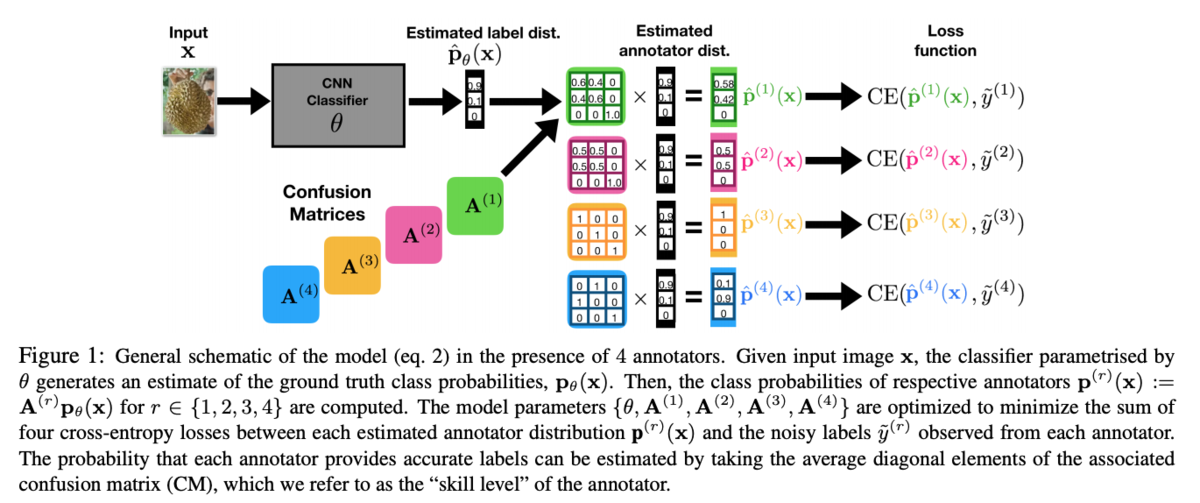
ここでは、以下の交差エントロピーの和を最小化することによって、アノテータ毎の推定CMと識別モデルの積$ \hat{\mathbf{p}}^{(r)}(\mathbf{x}) :=\hat{\mathbf{A}}^{(r)}\hat{\mathbf{p}}_{\theta} $がノイジーなラベルの分布に近くなるようにしていくのですが、このプロセスだけではアノテーターの推定CM $ \hat{\mathbf{A}} $と分類モデル$ \hat{\mathbf{p}} _ {\theta} $の組み合わせが無限にあるため、真の分布$ \hat{\mathbf{p}} _ {\theta}(\mathbf{x}) $からアノテーションノイズを分離することができません。ここでは、アノテータのCMについての正則化項を加えることによってこの一意性を確保しています。

$-\log p\left(\widetilde{\mathbf{Y}}^{(1)}, \ldots, \widetilde{\mathbf{Y}}^{(R)} | \mathbf{X}\right)=\sum_{i=1}^{N} \sum_{r=1}^{R} \mathrm{CE}\left(\mathbf{A}^{(r)} \hat{\mathbf{p}}_{\theta}\left(\mathbf{x}_{i}\right), \tilde{y}_{i}^{(r)}\right)$

Confusion Matrixにおいて、対角成分以外は誤分類にあたります。アノテータの真のCMと推定CMがdiagonally dominantであり( $ \left|a _ {i i}\right| \geq \sum _ {j \neq i}\left|a _ {i j}\right| \quad \text{for all } i $ (つまり、アノテーションによるノイズが多すぎないこと)))、かつ、識別モデルのCM( $ \boldsymbol{P} $ )についても$ \hat{\boldsymbol{A}} \boldsymbol{P}=\boldsymbol{A} $である(=誤分類のないような識別モデルがクリーンなデータに対して存在する)と仮定すると、アノテータの推定CMの対角成分はアノテータの真のCMの対角成分によって以下のように下限でバウンドされます。ここでは、識別モデルのCM( $ \boldsymbol{P} $ )が単位行列であることを利用しています。

$a_{i i}=\sum_{j} \hat{a}_{i j} p_{j i} \leq \sum_{j} \hat{a}_{i i} p_{j i}=\hat{a_{i i}}\left(\sum_{j} p_{j i}\right)=\hat{a}_{i i}$

これはつまり$ \operatorname{tr}(\mathbf{A}) \leq \operatorname{tr}(\hat{\mathbf{A}}) $であるので、この最小値はこの両辺が等しいときにユニークに満たされます。これを踏まえてCMの行列の対角成分の和であるTraceを以下のように正規化項として交差エントロピーの損失関数に加えることによって、アノテータのCMのより正確な推定を保証することができます。

$\sum_{i=1}^{N} \sum_{r=1}^{R} \mathbb{1}\left(\tilde{y}_{i}^{(r)} \in \mathcal{S}\left(\mathbf{x}_{i}\right)\right) \cdot \mathbf{C E}\left(\hat{\mathbf{A}}^{(r)} \hat{\mathbf{p}}_{\theta}\left(\mathbf{x}_{i}\right), \tilde{y}_{i}^{(r)}\right)+\lambda \sum_{r=1}^{R} \operatorname{tr}\left(\hat{\mathbf{A}}^{(r)}\right)$

実験セクションでは、MNISTデータを使って他のノイズにロバストなモデルとの比較をハイパーパラメータを変更しながら行なっています。比較的高い精度に加えて、Traceのパラメータ$ \lambda $にも強い影響を受けないことがわかります。この条件が満たされない場合、正規化項であるTrace Lossが交差エントロピーロスを上回ってしまうため、学習がうまくいきませんが、今回は低いロスに収束しています。

f:id:karolis_ml:20190725173645p:plain

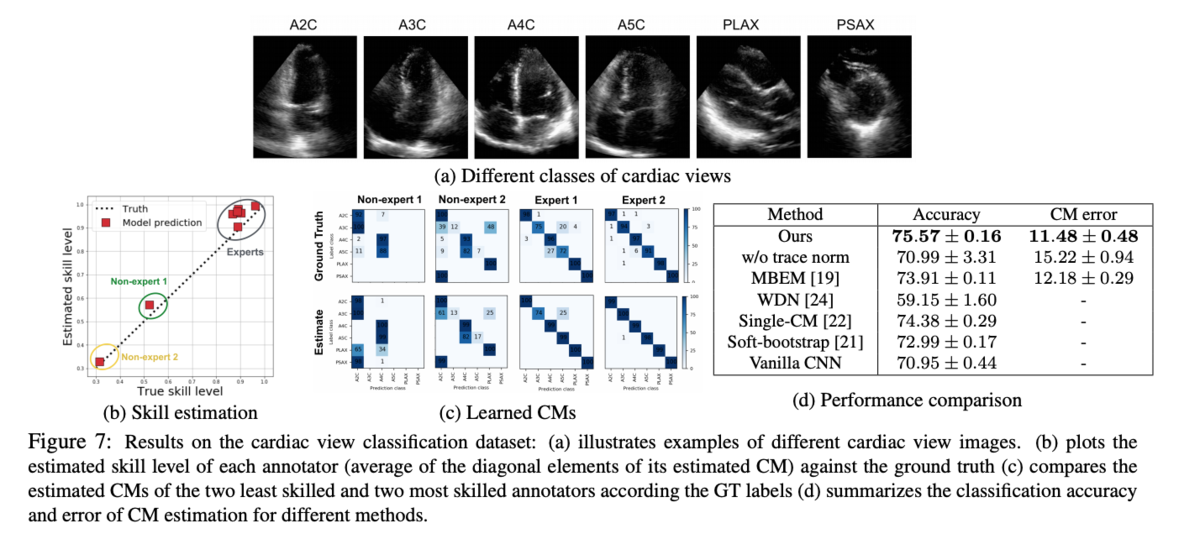
また、筆者らの応用データとして、6クラスの心電図への分類問題をこのアプローチを使って解いています。特にメディカル領域ではアノテーションの分散が大きくスキルのレベルの分散も大きいため、このようなアプローチが有用であると述べられています。図中(b)では、推定されたCMの対角成文の平均を推定スキルレベルとしてプロットしており、これが実際のスキルレベル(経験年数)と強く相関していることがわかります。

f:id:karolis_ml:20190725171625p:plain

個人的に、Traceを使った正規化とそれによるスキルレベルの推定はとても興味深いアプローチだと思いました。特にアノテータのスキルの分散が大きいメディカル分野において、これは非常に価値のあることだと思います。この手法はWisdom of the Crowd(多数決)と比べて理論的としても実験としても強い結果であるという印象ですが、現実世界でどれだけ複数アノテータのいるデータがあるかというと、またそれは別の問題ですね。

*余談ですが、この論文のSection 2.3. Motivation for Trace Regularizationのセクションで参照されているSukhbaatar et al. (2015)(ICLR 2015で発表)を読んでみたところ、Trace Regularizationのアイデア自体はほぼそのままLabel Noise Modellingの視点で書かれていました。今回のTanno et al. (2019)は、これをアノテーションによるノイズの分野に応用して複数アノテータへの拡張と実験をしているのですが、ここで何より驚いたのが、このアイデアとほとんど同じ構想と証明で論文を書いているSukhbaatar et al. (2015)の筆者らが、”Traceの実装が深層学習フレームワークにない”という理由で、実験セクションでは全てTraceをweight-decayによる正規化で置き換えている点です。

f:id:karolis_ml:20190727161828p:plain

Trace自体は簡単なコンセプトだと思うのですが、このペーパーがサブミットされた2014年当時はディープラーニング周りの実装が色々大変だったのかなぁ、というお気持ちを色々察してしまう結果となりました。ちなみにかのTensorflowが出てきたのが2015年です。

わざわざTraceで証明したのに... しかもその部分だけ実装して視点を変えたペーパーがCVPR...

ちなみに以下がSukhbaatarらの学習フレームワークです。少しわかりづらいですが、Tannoらが正規化項としてTraceと交差エントロピーを同時に最適化しているのに対して、こちらでは先にノイズの入ったデータを学習して(図の左半分)、ノイズ分をこのCMの正規化項で後から吸収する(図の右半分)というアプローチになっています。

f:id:karolis_ml:20190727162720p:plain

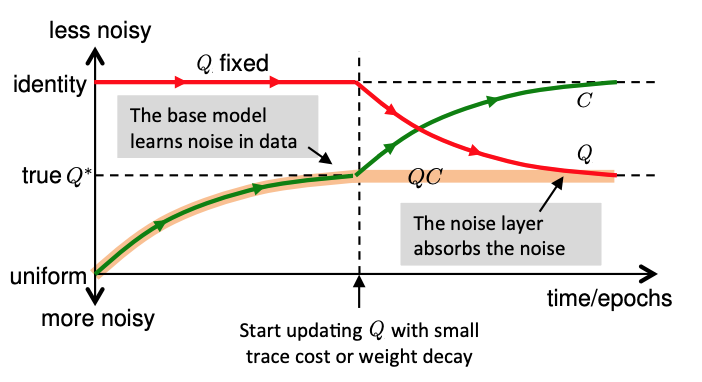
論文自体は以下にあるので時間のある方はこちらもご参照ください。

Sainbayar Sukhbaatar, Joan Bruna, Manohar Paluri, Lubomir Bourdev, and Rob Fergus., 2014, Training convolutional networks with noisy labels. arXiv preprint arXiv:1406.2080 https://arxiv.org/pdf/1406.2080.pdf

感想

こうして文献を見ていくと、基本的には実験セクションで試されているノイズの分布は一様もしくはクラス毎に率が違うといった程度のもので、現実的なアノテータからのノイズは心電図の分類をソノグラファーが行なったTanno et al. (2019)のみに留まりました。先ほども少し触れたように、論文の手法比較といった面では綺麗なデータセットにノイズを加えて実験するのが好ましいのでしょうが、実際のデータにどれだけこれらの手法が適応できるかはやはり難しいところです。まだまだここでは紹介しきれていないペーパーが数多くありますが、ある程度読んでいくと似たようなアプローチや手法、発想をしているペーパーも多く(Temporal ensembling/Mean Teacher/PSDRなど)、「本当にそれだけでSOTAなの?」みたいなものも多くありました。~~ハイパラチューニングしてるのかな~~。ここに関しては手元のノイジーなデータで実験してみるしかないですね。

特に、データセットによってはノイズ自体に重要な情報が含まれていることもある場合もあると個人的には思っているので、そのあたりを今回ご紹介したペーパーの手法も加味しながら解決していけるとよいなと思います。特に交差エントロピー損失に正規化項を加えるアプローチは実装も比較的簡単そうですね。

ただ、複数ネットワークの訓練における計算コストや、アノテーションを伴わないデータセットにおいてノイズの方が多い場合(i.e. Google Image検索)など、実際の応用においては多種多様な問題が想像できます。とてもつらい。

また、自然言語処理における感情センチメント分析等は、さらにラベルのノイズ問題が顕著になる印象です。こういったケースで厄介なのは、Computer Visionにおける画像分類問題と比べて、ラベルのInconsistencyがノイズによるものなのか、もしくはタスク自体が本質的に曖昧なのかがわかりづらいと言う点です。Toronto Faces Databaseでの表情ラベルのようなものも、タスク自体が曖昧と捉えることができると思います。こういった場合においては、ノイズとしてこれらのラベルを修正するよりは、アノテーターのドメイン知識や経験年数などを含めてラベルの分布や違い自体をモデリングしていくほうがよいイメージです。実際難しそうですが。

すごくどうでもいいことですが、Probably Approximately Correctって専門外の人に翻訳させたら「多分だいたいあってる」みたいなすごい適当な印象になりますね。ただこのノイジーラベルの文脈だと実際そんなお気持ちでモデルを組んでることもあるので冗談にはならないのが悲しいところ。

今回紹介しきれなかった論文や新しい研究、追加実験等もたくさんあるので、興味のある方はReferencesのペーパーの査読コメントや追加実験等を参考にしていただけると幸いです。

References

Arpit, D., Jastrzębski, S., Ballas, N., Krueger, D., Bengio, E., Kanwal, M.S., Maharaj, T., Fischer, A., Courville, A., Bengio, Y. and Lacoste-Julien, S., 2017, August. A closer look at memorization in deep networks. In Proceedings of the 34th International Conference on Machine Learning-Volume 70 (pp. 233-242). JMLR. org.

Angluin, D. and Laird, P., 1988. Learning from noisy examples. Machine Learning, 2(4), pp.343-370.

Bengio, Y., Louradour, J., Collobert, R. and Weston, J., 2009, June. Curriculum learning. In Proceedings of the 26th annual international conference on machine learning (pp. 41-48). ACM.

Chatterjee, S., 2018, "Learning and Memorization"

Chang, H.-S., Learned-Miller, E., and McCallum, A., 2017, Active bias: Training a more accurate neural network by emphasizing high variance samples. NIPS.

Chen, P., Liao, B., Chen, G. and Zhang, S., 2019. A Meta Approach to Defend Noisy Labels by the Manifold Regularizer PSDR. arXiv preprint arXiv:1906.05509.

Grandvalet, Y. and Bengio, Y., 2005. Semi-supervised learning by entropy minimization. In Advances in neural information processing systems (pp. 529-536).

Gretton, A. Smola, J. Huang, M. Schmittfull, K. Borgwardt, and B. Scholkopf., 2009, “Covariate shift by kernel mean match- ¨ ing,” in Dataset shift in machine learning (J. Quinonero-Candela, M. Sugiyama, A. Schwaighofer, and N. Lawrence, eds.), ch. 8, pp. 131–160, MIT press.

Han, B., Yao, Q., Yu, X., Niu, G., Xu, M., Hu, W., Tsang, I. and Sugiyama, M., 2018. Co-teaching: Robust training of deep neural networks with extremely noisy labels. In Advances in neural information processing systems (pp. 8527-8537).

Jiang, L., Zhou, Z., Leung, T., Li, L.J. and Fei-Fei, L., 2017. Mentornet: Learning data-driven curriculum for very deep neural networks on corrupted labels. arXiv preprint arXiv:1712.05055.

Laine, S. and Aila, T., 2016. Temporal ensembling for semi-supervised learning. arXiv preprint arXiv:1610.02242.

Li, Y., Yang, J., Song, Y., Cao, L., Luo, J. and Li, L.J., 2017. Learning from noisy labels with distillation. In Proceedings of the IEEE International Conference on Computer Vision (pp. 1910-1918).

Liu, T. and Tao, D., 2015. Classification with Noisy Labels by Importance Reweighting. IEEE Transactions on pattern analysis and machine intelligence, 38(3), pp.447-461

Malach, E. and Shalev-Shwartz, S., 2017. Decoupling" when to update" from" how to update". In Advances in Neural Information Processing Systems (pp. 960-970).

Oliver, A., Odena, A., Raffel, C.A., Cubuk, E.D. and Goodfellow, I., 2018. "Realistic evaluation of deep semi-supervised learning algorithms". In Advances in Neural Information Processing Systems (pp. 3235-3246).

Sainbayar Sukhbaatar, Joan Bruna, Manohar Paluri, Lubomir Bourdev, and Rob Fergus., 2014, Training convolutional networks with noisy labels. arXiv preprint arXiv:1406.2080

Suzuki, T., 2012, "統計的学習理論のチュートリアル: 基礎から応用まで"　

Reed, S., Lee, H., Anguelov, D., Szegedy, C., Erhan, D. and Rabinovich, A., 2014. Training deep neural networks on noisy labels with bootstrapping. arXiv preprint arXiv:1412.659.

Tanaka, D., Ikami, D., Yamasaki, T. and Aizawa, K., 2018. Joint optimization framework for learning with noisy labels. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (pp. 5552-5560).

Tanno, R., Saeedi, A., Sankaranarayanan, S., Alexander, D.C. and Silberman, N., 2019. Learning From Noisy Labels By Regularized Estimation Of Annotator Confusion. arXiv preprint arXiv:1902.03680.

Tarvainen, A. and Valpola, H., 2017. Mean teachers are better role models: Weight-averaged consistency targets improve semi-supervised deep learning results. In Advances in neural information processing systems (pp. 1195-1204).

Natarajan, N., Dhillon, I.S., Ravikumar, P.K. and Tewari, A., 2013. Learning with noisy labels. In Advances in neural information processing systems (pp. 1196-1204)

Nock, R. and Nielsen, F., 2009, “Bregman divergences and surrogates for learning,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 31, no. 11, pp. 2048–2059.

ABEJA Tech Blog

中の人の興味のある情報を発信していきます

ノイズのある教師データを用いた機械学習に関する研究サーベイ