はじめに

このブログに書かれていること

前半（前半ブログはこちら）
- 古代暗号から始まる暗号の歴史
- エニグマの構造と解読法について
後半
- RSA暗号の基本
- 楕円曲線暗号の基本

自己紹介

こんにちは！株式会社ABEJAの @Takayoshi_ma です。前半では暗号の歴史について書いていきました。後半はRSA暗号や楕円曲線暗号についての基本的な知識についてまとめたブログとなっています。尚、前半部分から読みたいよ！っていう方はこちらからよろしくお願いします。

注意

本ブログで書かれているサンプルコードのセキュリティ強度は保証できません。あくまでも例として書いているだけなのでご注意ください。

Part3 現代の暗号

ここからは現代のコンピュータ社会で広く使われる暗号について解説していきます。

共通鍵暗号方式と鍵配送問題

鍵配送問題とは？

ここまで紹介してきた暗号方式は全て共通鍵暗号方式と呼ばれるカテゴリーに属します。共通鍵暗号方式とは

暗号化に使われる鍵と復号に使われる鍵が同じ

上記の様に表現できます。ここで問題になってくるのが鍵配送問題です。例えばエニグマでは鍵の情報（使用されるローターとその初期設定）を発信者と受信者の間で事前に共有しておく必要があります。しかしこの共有されたコードブックを何者かに奪われるといった可能性も否定できません。そうなると暗号が筒抜けになってしまう可能性もあります。このようにどんなに複雑な鍵だとしてもその情報がバレてしまうと、簡単に暗号は突破されてしまいます。そのような問題を解決したのが公開鍵暗号方式です。

共通鍵暗号方式と公開鍵暗号方式の違いとメリット・デメリット

ここでは公開鍵暗号方式とはどの様な仕組みかを簡単に紹介します。公開鍵方式とはざっくりした日本語で表現すると

暗号化に使われる鍵（公開鍵）と復号に使われる鍵（非公開鍵）が異なる
公開鍵からは非公開鍵を特定できない

となります。この仕組みが実現すると以下の図のように暗号化に使われる鍵が第三者に漏洩してしまった場合でも、それを復号するための鍵さえバレなければ暗号を解読することができない。言い換えれば復号鍵を発信者に対して配送する必要がないというメリットがあります。よって、公開鍵暗号方式は、以前より問題となっていた鍵配送問題に対して有効な対策となります。では鍵配送問題がつきまとう共通鍵暗号方式にはどの様なメリットがあるのでしょうか？

その答えの一つが処理スピードの速さです。例えば有名どころではSSL通信、こちらは共通鍵暗号方式と公開鍵暗号方式の良いとこ取りをしたハイブリッド型の暗号方式となります。

手順1
- HTTPSリクエスト(WEBブラウザ→WEBサーバ)
- WEBブラウザからWEBサーバへ[https://]によるアクセスを開始
手順2
- SSLサーバ証明書を送信(WEBサーバ→WEBブラウザ)
- WEBサーバから以下の情報をWEBブラウザ側へ送信
- 中間CA証明書および中間認証局の公開鍵
- SSLサーバ証明書およびWEBサーバの公開鍵
手順3
- ルート証明書による照合(WEBブラウザ)
- ルート認証局の公開鍵で中間CA証明書を復号して中間認証局の公開鍵を取り出す
- 中間認証局の公開鍵でSSLサーバ証明書を復号してWEBサーバの公開鍵を取り出す
- 共通鍵を生成しWEBサーバの公開鍵で暗号化してWEBサーバへ送信する
手順4
- 共通鍵の送信(WEBブラウザ→WEBサーバ)
- WEBブラウザにて暗号化された共通鍵を送付する
- 暗号化した共通鍵をWEBサーバに送信
手順5
- 共通鍵による通信(WEBサーバ)
- 共通鍵を秘密鍵で復号する
手順6
- 共通鍵による通信(WEBブラウザ⇔WEBサーバ)
- WEBブラウザによって作成された共通鍵いより暗号化通信を実現

上記の流れでセキュアかつ高速な通信を可能にします。

RSA暗号

ここからは公開鍵暗号方式の代表的な手法であるRSA暗号について解説します。様々な場面で使用されている暗号方式で皆さんにも馴染みの深いものだと思います。ここではそのRSA暗号について、具体例を交えながら手順を追っていった後、その数学的背景について、数式をゆっくり一つ一つ追いながら理解していきます。

始めに今回の例を書き記しておきます。例で記されている数列は適当に入れていますが、どの数も後述の公開鍵 $n$ 未満である必要があります。RSA暗号では巨大な $n$ を使うことになるので、特に気にする必要はありません。

送りたい平文： LOVE

平文を数字に直した数列： 26 9 20 13

RSAで使われる鍵

まず送信者は公開鍵を使って平文26 9 20 13　を暗号化しないといけません。そこで受信者はあらかじめ秘密鍵と公開鍵のペアを作成し、そのうち公開鍵の方を送信者へ共有する必要があります。RSA暗号では巨大な素数を2つ用意します。本来この素数はものすごく大きな数である必要があるのですが、ここでは簡単に以下の2つを秘密鍵とします。

$\displaystyle \begin{eqnarray} p &=& 5 \\ q &=& 11 \\ \end{eqnarray}$

次にこの秘密鍵から公開鍵を生成します。公開鍵は2つ必要でそれぞれの定義は以下のとおりです。

公開鍵１　 $n$ ：　 $p$ と $q$ の積

公開鍵２　 $e$ ：　 $(p-1)(q-1)$ と互いに素な数

定義より $n$ は以下のように求まります。

$\displaystyle n = pq = 55$

また $e$ は一般に複数パターンが存在しますが、ここでは仮に以下のように定義します

$\displaystyle e = 3　(40と互いに素)$

公開鍵１の定義だけ見ると、公開鍵が分かってしまえば、その値を素因数分解することで秘密鍵のペアも判明してしまいそうに感じるかもしれませんが、実際には非常に巨大な数の素因数分解となるため、膨大な計算量を要してしまいます。つまり公開鍵が分かったところで、秘密鍵がわかることは無い、セキュリティの高い鍵だと言えることが分かります。その代わり二つの秘密鍵さえ決めて仕舞えば、その積を取るだけで公開鍵を計算できることも注目すべきポイントです。

処理手順

暗号化の手順

暗号化したい整数を $x$ とすると暗号後の整数 $x$ は2つの公開鍵を使って、以下のように定義されます。

$\displaystyle y = x^e (\bmod n)$

先ほどのloveを暗号化すると以下の整数列に変換されます。

$\displaystyle \begin{eqnarray} y_0 &=& 26^3 (\bmod 55) = 31 \\ y_1 &=& 9^3 (\bmod 55) = 14 \\ y_2 &=& 20^3 (\bmod 55) = 25 \\ y_3 &=& 13^3 (\bmod 55) = 52 \\ \end{eqnarray}$

上記の計算を行うと、平文26 9 20 13は31 14 25 52へと暗号化されます。

復号の手順

受信者は秘密鍵を使って以下の整数をあらかじめ用意します。

$\displaystyle L:　\operatorname{lcm}(p-1, q-1)$

$\displaystyle d:　一次不定式 de-yL=1 の自然数解(d, y)$

$L$ に関しては２数の最小公倍数を求めるだけなので、今回の例で言えば $20$ となることに、特に問題ないかなと思います。 $d$ に関しては、なぜこのような数を使うのか。その数学的背景は後ほど解説するとして、ここでは以下のような数が解となり得ることを確認しておけばOKです。もちろん他の自然数解でも問題ありません。

$\displaystyle (d, y) = (7, 1)$

$\displaystyle de - yL = 7×3 - 1×20 = 1$

これで復号に必要な情報が揃いました。暗号化後の整数を $y$ とすると復号後の整数 $x$ は以下の式で求まります。

$\displaystyle x = y^d (\bmod n)$

実際に計算してみると

$\displaystyle \begin{eqnarray} x_0 &=& 31^7 (\bmod 55) = 26 \\ x_1 &=& 14^7 (\bmod 55) = 9 \\ x_2 &=& 25^7 (\bmod 55) = 20 \\ x_3 &=& 52^7 (\bmod 55) = 13 \\ \end{eqnarray}$

となり、正しく復号できていることが確認できます。

RSA暗号の数学的背景

暗号化・復号の手順を追ってきましたが、ここで以下の2点を確認する必要があります。

そもそもなぜこの式で元の平文に戻るのか？
一次不定式 $de-yL=1$ は絶対に自然数解を持つことが保証できるのか？

それでは順を追って解説していきます。

一次不定式が自然数解を持つ理由

まず始めに以下を確認する必要があります。

$a$ と $b$ が互いに素なとき、以下の一次不定式は整数解をもつ

$\displaystyle ax - by = 1$

上記を確認する前に以下の定理が成り立つことを確認しておきます。

$\gcd(a, b) = c$ としたとき一次不定式　 $ax+by=ck$ （ $k$ は任意の整数）　は整数解をもつ

例えば $a=4$ 、 $b=6$ とするとその最大公約数は $2$ となります。そして以下の一次不定式の右辺は $2$ の倍数であることから、整数解を持つことが分かります。

$a$ と $b$ が互いに素なとき、以下の一次不定式は整数解をもつ

$\displaystyle 4x + 6y = 10$

実際、上記の一次不等式は

$\displaystyle (x, y) = (4, -1)$

という整数解が存在しますが、（具体例を1つあげただけで、もちろん他の解も無数に存在します）

$\displaystyle 4x + 6y = 15$

のように右辺が最大公約数2の倍数でない場合、整数解は存在しません。上式を見てみるのが一番分かりやすいですが、左辺が2の倍数になることが明らかな一方（どの項も最大公約数である2の倍数になっているのでそれを足しても2の倍数になる）、右辺は2の倍数とおらず矛盾していることが明らかです。厳密な証明はここでは省きますが、下記のサイトが非常に良くまとめられていますので、そちらをご参照ください。

https://manabitimes.jp/math/674

よって、このとこから　 $de-yL=1$ 　が整数解をもつためには、 $e$ と $L$ が互いに素である（つまり最大公約数が1である）必要があることが分かります。

eとLの関係性

説明に入る前に以下少しだけ補足です。

（補足パート）文献によっては、 $e$ の定義を以下のように定めているものもあるかもしれませんが、結局「 $a$ と $b$ が互いに素」、かつ「 $a$ と $c$ が互いに素」なとき、「 $a$ と $bc$ は互いに素」であるので、同じことを示しています。

$\displaystyle e:　(p-1)、及び(q-1)の両方の数と互いに素である数$

それでは本題に入ります。 $e$ と $L$ が互いに素であることは、背理法によって証明可能です。まず $e$ についてですが、こちらは定義より整数 $(p-1)(q-1)$ と互いに素であることが与えられています。よって以下のことが言えます。

$\displaystyle \gcd(e, (p-1)(q-1)) = 1$

また、 $L$ は $(p-1)(q-1)$ の最小公倍数と定義されていますが、一般に $a$ と $b$ の最小公倍数と最大公約数の積は $a$ と $b$ の積と等しくなることから、その関係は次のようになります。

$\displaystyle L = \operatorname{lcm} \left( (p-1), (q-1) \right) =\frac{(p-1)(q-1)}{\gcd \left( (p-1), (q-1) \right)}$

ここで、 $L$ の形式に注目します。 $L$ は $(p-1)(q-1)$ を $\gcd \left( (p-1), (q-1) \right)$ で割ったものです。 $e$ と $(p-1)(q-1)$ が互いに素であることから、 $e$ と $L$ の最大公約数は $(p-1)(q-1)$ の約数である必要があります。しかし、 $\gcd \left( (p-1), (q-1) \right)$ は $(p-1)(q-1)$ の約数であり、 $e$ と $(p-1)(q-1)$ が互いに素であることから、 $e$ と $\gcd \left( (p-1), (q-1) \right)$ も互いに素でなければなりません。したがって、 $e$ と $L$ の最大公約数は1である必要があります。

前置きが長くなってしまいましたが、このことより一次不定式 $de-yL=1$ は絶対に整数解を持つことが分かります。もちろん正負の記号どちらも取りうることが可能ですが、最終的に復号に必要な $d$ は必ず正の数である必要があるので、そのような $d$ を一つ選択する必要があります。

そもそもなぜこの式で元の平文に戻るのか？の数学的根拠

証明パート１

定義より、一度暗号化したものを復号して元に戻るという操作は以下の式で表すことができます。

$\displaystyle x^{de} \equiv x \pmod n$

つまり、 $d$ 乗して更にそれを $e$ 乗して出てきた整数は元の整数 $x$ と $n$ を法として合同であることが証明できればOKです。

ここで

$\displaystyle \begin{eqnarray} de - yL &=& 1 \\ de &=& yL + 1 \\ \end{eqnarray}$

より

$\displaystyle x^{de} = x^{yL + 1} = x \cdot x^{yL}$

$\displaystyle \begin{eqnarray} x \cdot x^{yL} &\equiv& x \pmod n \\ &\equiv& x \pmod {pq} \cdots ☆ \\ \end{eqnarray}$

と表せます。以降、この☆式を証明していきます。

フェルマーの小定理

ここから先の証明で必要になるので、一旦脇道にそれますがフェルマーの小定理について解説していきます。フェルマーの小定理は、整数 $a$ と素数 $p$ が互いに素なとき、以下の式が成り立つという定理です。

$\displaystyle a^{(p-1)} \equiv 1 \pmod p$

分かりやすいように具体例を書いていきます。今 $\pmod p$ の世界における話をしていますが、例えば素数 $p=5$ としたとき、この世界には0, 1, 2, 3, 4の4つの数しか存在しません。また素数は1以外に約数を持たないことから以下も分かると思います。

$\displaystyle 1, 2, 3, 4, いずれの整数も 5 と互いに素$

つまり

$\displaystyle 1, 2, 3, \cdots (p-1), いずれの整数も p と互いに素$

今、 $a$ も $p$ と互いに素であることを考えると、上記の数列と $a$ を掛け算しても $p$ との共通因子を持たないことが明らかなので、

$\displaystyle a, 2a, 3a, \cdots a(p-1), いずれの整数も p と互いに素$

ということが分かります。そして実は上記の数列の $\mod p$ は全て異なる整数になることが分かります。例えば上の例だと

$\displaystyle \begin{eqnarray} 1 \pmod5 &\equiv& 1 \\ 2 \pmod5 &\equiv& 2 \\ 3 \pmod5 &\equiv& 3 \\ 4 \pmod5 &\equiv& 4 \\ \end{eqnarray}$

となり、全て異なる数が出現しています。何故そうなるかは背理法で証明できます。

整数 $i$ と $j$ が $1\le i\le j\le p-1$ をみたすとき、

$\displaystyle ja - ia = (j-i)a$

であり、 $a$ は $p$ と互いに素であることと、 $0\le j-i\le p-2$ であることから、 $ia\equiv ja\pmod p$ である必要十分条件は $i=j$ でなければならず、結局 $i$ と $j$ が異なると違った整数になることが示されました。

よって $\mod p$ において

$\displaystyle a\cdot 2a \cdots(p-1)a \equiv 1\cdot 2\cdots (p-1)$

となり上式の左辺と右辺が $p$ を法として、合同であることが分かります。この式を書き換えると

$\displaystyle a^{p-1}(p-1)! \equiv (p-1)!\pmod p$

となります。ここからAtCoder頻出の逆元の考え方を利用します。今 $p$ が素数であることから、 $(p-1)!$ と $p$ は互いに素なので、上式の両辺に逆元をかけることで $(p-1)!$ を打ち消し合うことができます。

$\displaystyle a^{p-1}\equiv 1 \pmod p$

この辺りの詳しい解説はこちらのブログが非常に参考になると思います。

中国剰余定理

ここで、パート１で出てきた☆式をもう一度眺めてみます。

$\displaystyle \begin{eqnarray} x \cdot x^{yL} &\equiv& x \pmod n \\ &\equiv& x \pmod {pq} \cdots ☆ \\ \end{eqnarray}$

少し、先回りになってしまいますが実は中国剰余定理（二元の場合）と呼ばれる定理において

$n_1$ と $n_2$ が互いに素なとき、

$\displaystyle x\equiv a_1 \pmod{n_1}$

$\displaystyle x\equiv a_2 \pmod{n_2}$

を満たす $x$ が $0$ 以上 $n_1n_2$ 未満の範囲にただ1つだけ存在することが分かっています。具体例を挙げると、 $3$ で割り算した時に余りが $2$ 、 $5$ で割り算したときに余りが $4$ である数は $15(= 3 \cdot 5)$ 以内に1つだけ存在する。と言うことです。数えてみれば分かりますが、この場合 $14$ しか条件を充す整数がないことが分かります。

中国剰余定理の証明は長くなるので割愛します。気になる方は以下のサイトをご参照ください。

https://manabitimes.jp/math/837

これを一旦、頭に入れた上で☆式の解説を進めていきます。☆式とは少し形が違いますが、今次式について考えていきます。

$\displaystyle x \cdot x^{yL} \equiv x \pmod p \cdots ★$

後述ですが、上式が常に成り立つことを示すことができれば☆式についても成り立つことが中国剰余定理を応用して証明可能となります。そこで上式について深掘りしていきます。

まず、簡単なパターンですが、 $x$ が $p$ の倍数であるときですが、上式は左辺も右辺も $0$ となるので、正しいことが分かると思います。次に難しいパターンを証明していきます。このとき $x$ は $p$ の倍数ではありません。そのことを頭に置いて式変形していきます。

$\displaystyle x \cdot x^{y(p-1)k} \equiv x \pmod p \cdots kは何かしらの定数$

上の変換は $L=\operatorname{lcm}(p-1, q-1)$ より $L$ が $(p-1)$ の整数倍であることを利用しています。ここでフェルマーの小定理を利用すると、

$\displaystyle x^{y(p-1)k} = (x^{p-1})^{yk}$

より

$\displaystyle (x^{p-1})^{yk} \equiv 1 \pmod p$

となります。なぜならば $p$ が素数で、 $x$ と $p$ が互いに素（倍数ではないので必然的にそうなる）だからです。ちなみに $\pmod p$ における和・差・積はそれぞれの成分の $mod$ の和・差・積と同じであることも併せて利用しています。これもAtCoder頻出。

よって、★式は以下のようになり証明完了です。

$\displaystyle x \cdot 1 \equiv x \pmod p \cdots ★$

また、同様に $p$ と同じ条件である、 $q$ についても成り立つことが分かるかと思います。

$\displaystyle x \cdot x^{yL} \equiv x \pmod q \cdots ★$

ここで先ほどの中国剰余定理を利用すると、以下のことが言えます。

整数 $x^{yL}$ を $pq$ で割った時の余りは $0$ 以上 $pq$ 未満の間に一つだけ存在する。

ここでまでは問題ないかと思います。ではその数はなんでしょうか？今、上の二つの★式を見てみると分かるのですが、 $p$ で割っても $q$ で割っても、余りは $x$ であることがわかると思います。つまり $pq$ と言う積で表される整数で割ってもその余りは $x$ 以外に存在しないということが逆説的に導かれることになります。

よってここでようやく以下の☆式が証明され、RSA暗号を使った復元化の原理が証明できたことになります。

$\displaystyle \begin{eqnarray} x \cdot x^{yL} &\equiv& x \pmod {pq} \cdots ☆ \\ &\equiv& x \pmod n \cdots ☆ \\ x^{de} &\equiv& x \pmod n \cdots ☆ \\ \end{eqnarray}$

RSA暗号をPythonで

実際にPythonで書くとこのような形になります。

from Cryptodome.PublicKey import RSA
from Cryptodome.Cipher import PKCS1_OAEP
from Cryptodome.Random import get_random_bytes

# 鍵ペアの生成
key = RSA.generate(2048)

# 公開鍵と秘密鍵の取得
private_key = key.export_key()
public_key = key.publickey().export_key()

# 公開鍵での暗号化
plain_text = '男は黙ってサッポロビール'
plain_text = bytes(plain_text.encode('utf-8'))
recipient_key = RSA.import_key(public_key)
cipher_rsa = PKCS1_OAEP.new(recipient_key)
encrypted_message = cipher_rsa.encrypt(plain_text)
print(f'Encrypted message: {encrypted_message}')

# 秘密鍵での復号
decryption_key = RSA.import_key(private_key)
cipher_rsa = PKCS1_OAEP.new(decryption_key)
decrypted_message = cipher_rsa.decrypt(encrypted_message)
print(f'Decrypted message: {decrypted_message.decode("utf-8")}')

結果

Encrypted message: b"B\xff\x88gC\x0eu\xea5X\xb3p&\xd1\xd1\xe57R\xa4\xf1\xba\\*\xc07\xbdj:\xbf\x19\x12w\xfa\x9e\xb1\xd7\xc4i\x12\xca4\xa9\xc7\x8ci\x98\xc5\x99\xae\xf4\x8f\xd7(l\xff\x99*D\x18\xc87ix\xd9H\xc9\xa0\xa0D*\x85\x7f\x8e\x19X\x0e\xbe\xf7\xe4\x84\x96\xaa\xfc^-\xb4\x04\xff\x13\xfa\x90t\xdbd\xe64\x9e\xbe\xd6\xfcx\x0c-\x18k\x966\xa6\x01\xcfeP\xd0{\xa4\xf2%r\xdb\xc0V\xd9\x07\xce\x9c\xb7\x1a\x0e\xb2J\xad\xced\xd5\xa6\x8ex\x0e\xd4Y\xae].\xd4@po\x8d\xf7\xe6_\xf2 \xcb\xce[\x8e\xef0\xf5\xbc_\xdd\x9b\xbbK\xcd\x1e\x82\x83imHT\xfb\x83\xf3\xd5\x8d-Y9\xec\x1f\xcd\x06\xc1\xcc\xf0N\xd9\xf2-\x13\x8e\x0cf\x02|\x04i\x83:\xe7]\xad\xb1@\xbd?\x8b\x85\xafd\xe0`nK\xdf\xc7\xe3\x84F\x08\xc0=7\xb1\x1c\xfea\xeb\xb8\xf0's\xbd\xef\x10\x19\xdf\x1c\xff\xe9\xfb\xddz+x>\x05\xa0\xc7\xe0\xf1S"
Decrypted message: 男は黙ってサッポロビール

尚、上のコードではPKCS1_OAEPを使ってOAEPパディングを適用しています。OAEPは、RSA暗号化において、パディングとして使用されるスキームの一つです。このパディングは、暗号文をより安全にすることを目的として、平文メッセージの周囲に追加のデータを付加します。

楕円曲線暗号

楕円曲線とは？

楕円曲線の式

ここから先は楕円曲線暗号について、取り上げていきたいと思います。RSA暗号よりもより少ないbit長でセキュアな鍵を作れるアルゴリズムであり、暗号資産関連やSSL通信など多くの場面で採用されいます。

楕円曲線は以下の数式で表されます。

$\displaystyle y^2 = x^3 + ax + b$

$a$ や $b$ はパラメータですが、例えばビットコインやイーサリアムにおけるECDSA署名には以下の楕円曲線（secp256k1 ）が採用されています。

$\displaystyle y^2 \equiv x^3 + 7 \pmod {2^{256} - 2^{32} - 977}$

$a = 0$ 、 $b = 7$ はいいとして、なぜいきなり $mod$ ？と思われるかもしれませんが、理由は後述するとして一旦先に進めます。楕円曲線は $a$ と $b$ のパラメータによって以下のように様々な形を取ります。[tex: y²]が用いられていることにより、 $x$ 軸に対して上下が反転する形になっているのがポイントです。

画像はwikipediaより抜粋： https://ja.wikipedia.org/wiki/%E6%A5%95%E5%86%86%E6%9B%B2%E7%B7%9A

暗号に使用される楕円曲線にはちゃんとした $a$ 、 $b$ の定義があるようなのですが今回は割愛します。

楕円曲線における足し算の定義

以下のPythonコードで記述した楕円曲線を例に、足し算の定義を説明していきます。

import numpy as np
import matplotlib.pyplot as plt


# 楕円曲線のパラメータを指定
# p = 67  # 素数
a = 0
b = 1

# 楕円曲線の方程式を定義
def curve(x, y):
    return y**2 - x**3 - a*x - b

# プロット領域を作成
fig, ax = plt.subplots()

# 楕円曲線を描画
x_range = np.linspace(-4, 4, 100)
y_range = np.linspace(-4, 4, 100)
x, y = np.meshgrid(x_range, y_range)
c = ax.contour(x, y, curve(x, y), levels=[0], colors='red')

# グラフの設定
ax.set_aspect('equal')
ax.set_xticks(range(-4, 4, 1))
ax.set_yticks(range(-4, 4, 1))
plt.grid()
plt.show()

以下は、点 $P$ と点 $Q$ の足し算を行った $P+Q$ の座標を表します。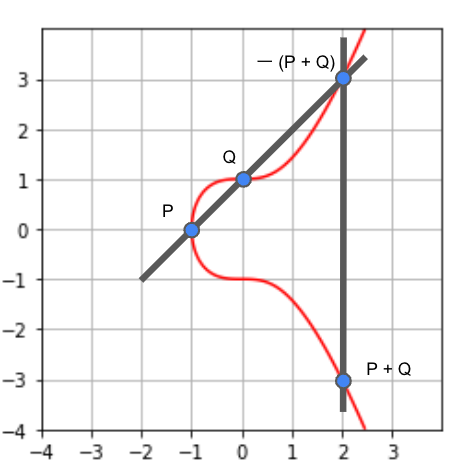求め方の手順は以下の通りです。

始めに $P$ と $Q$ を直線で結ぶ
その直線と楕円曲線が交わる点を見つける
その点を $x$ 軸に対して反転させた点を $P+Q$ とする

次に掛け算ですが以下は点 $P$ を2倍した $2P$ の座標になります。求め方の手順は以下の通りです。

$2P=P+P$ とする
$P$ と $P$ を結ぶ直線、つまり $P$ の接戦を引く
この直線と楕円曲線が交わる点を見つける
その点を $x$ 軸に対して反転させた点を $2P$ とする

楕円曲線における引き算の定義

結論から先に述べると楕円曲線における引き算ですが、例えば以下のような形で処理します。

$\displaystyle P - Q = P + (-Q)$

つまり $P$ から $Q$ を引き算したい、 $P$ と $-Q$ を足し算する形で求めます。

無限遠点

次に無限遠点と呼ばれる概念について軽く触れます。無限遠点ですが、書いて字のごとく、どこまでも果てしなく続く遠くの点のようなイメージです。

$\displaystyle O(\infty, \infty)$

そして無限遠点の大切な性質ですが、楕円曲線における無限遠点は単位元となります。つまり $P$ に無限遠点を足しても元の $P$ のまま変わらないと言う性質があります。

$\displaystyle P + O = P$

ここで何故、 $x$ 軸に対して反転させた点を負の数と捉えるかについてですが、以下のような例で考えていきたいと思います。

ここで点 $P$ と $P$ を反転させた点 $Q$ を結ぶ直線はどこまで行っても楕円曲線と3つ目の点で交わることはありません。これを

点 $P$ と $P$ を反転させた点 $Q$ を結ぶ直線は楕円曲線と無限遠点で交わる

と定義すると、その足し算について以下のように表すことができます。

$\displaystyle P + Q = O$

$\displaystyle Q = -P$

楕円曲線における分配法則と交換法則

楕円曲線のもう一つ大事な性質として通常の整数の足し算と同じように分配法則や交換法則が成り立つ点があります。具体例を示すと

分配法則：
- $P+P+P+P$ と $(P+P)+(P+P)$ は等しい
交換法則：
- $P+Q+P+Q+P$ は $P+P+P+Q+Q$ と等しい

以下の部は分配法則が成り立つことを表した図になります。多少ずれているように見えないこともないですが、それはGoogleSlideの限界なだけで、本当はピッタリ一致します。

これを利用することで例えば $2^{256}P$ のような非常に大きな数との掛け算も高速に求めることが可能です。

まず $2P = P + P$ を求める
次に $4P = 2P + 2P$ を求める
次に $8P = 4P + 4P$ を求める
...

つまり $O(logN)$ の計算量です。後述ですが、この性質を利用することで秘密鍵から公開鍵の生成を高速に行うことが可能となっています。

楕円曲線の加法を式で表現

楕円曲線上の足し算についてその定義を説明してきましたが、今度は式で表現していきたいと思います。

点Pと点Qが異なる場合

楕円曲線 [tex: E: y² = x³ + ax + b]上の異なる点 $P(x_1, y_1)$ と $Q(x_2, y_2)$ の2点を通る直線 $L$ の方程式は

$\displaystyle L: y - y_1 = \dfrac{y_1-y_2}{x_1-x_2}(x-x_1)$

となる。少し見にくいので、以降この直線の傾き $\dfrac{y_1-y_2}{x_1-x_2}$ を $\lambda$ とおく。この直線と楕円曲線の交点は

$\displaystyle \biggr\{ \lambda(x-x_1) + y_1 \biggr\}^2 = x^3 + ax + b$

ここで三次方程式の根を３つ足し合わせたものが

$\displaystyle -\dfrac{3次の係数}{4次の係数}$

になることより（この辺の証明については以下のサイトに委ねます、この辺の解説があやふやになってるサイトも多いと思ったので、一応根拠も掲載しておきます。）

https://hiraocafe.com/note/kaitokeisuu3ji.html

上記の方程式が３つの根 $x_1$ , $x_2$ , $x_3$ を持つときその和は

$\displaystyle x_1 + x_2 + x_3 = \lambda^2$

このことから点 $P+Q(x_3, y_3)$ の座標は

$\displaystyle \begin{eqnarray} x_3 &=& \lambda^2 - x_1 - x_2 \\ &=& \biggl( \dfrac{y_1-y_2}{x_1-x_2} \biggr)^2 - x_1 - x_2 \\ y_3 &=& y_1 + \lambda(x_3-x_1) \\ &=& y_1 + \biggl( \dfrac{y_1-y_2}{x_1-x_2} \biggr) (x_3-x_1) \\ \end{eqnarray}$

となります。

点Pと点P 同じ点を足し合わせる場合

点 $P(x_1, y_1)$ 、点 $2P(x_3, y_3)$ とします。この時 $P$ の接線の傾きは

$\displaystyle \dfrac{dy}{dx} = \dfrac{3x^2+a}{2y} = \lambda$

ここから先は先ほどと同じような形で式変形をしていきます。最終的に求められる式の形も同じですが、 $\lambda$ の求め方が少し違ってきていることに注意が必要です。

$\displaystyle \begin{eqnarray} x_3 &=& \lambda^2 - x_1 - x_2 \\ &=& \biggl( \dfrac{3x_1^2+a}{2y_1} \biggr)^2 - 2x_1 \\ y_3 &=& y_1 + \lambda(x_3-x_1) \\ &=& y_1 + \biggl( \dfrac{3x_1^2+a}{2y_1} \biggr) (x_3-x_1) \\ \end{eqnarray}$

有限体

有限体とは？

先ほどの説明でビットコインで使われる楕円曲線を挙げた際に、合同式が出てきたと思いますが、ここではその理由について書いていきます。そもそもなぜ合同式を使うのか？その大きな理由はコンピュータが無限に大きな数やどこまでも果てしなく続く有理数を扱うことができないと言う理由が一番の要因です。前者については言わずもがな、後者については少数や分数を扱うことで誤差などの影響が非常に大きくなってきてしまうことに起因します。

有限体の厳密な定義については自身の理解が追いついていない部分も多く他文献に解説を委ねようと思いますが、例えば以下のモジュラー演算において、 $x$ が整数であることを前提条件とすると、 $z$ が取りうる値の範囲が $0$ から $p-1$ の範囲の自然数に限定されていることが分かります。つまり $z$ は有限体（有限個の元からなる体）と言えます。

$\displaystyle z = x^3 + 7 \pmod p$

またこの時、有限体がとりうる値のパターン数を位数と言います。

有限体上の楕円曲線

ここでは例として有限体上の楕円曲線を可視化してみます。愚直ですが下記のように $p$ までの範囲内で全探索していきます。

import itertools

import matplotlib.pyplot as plt


def get_points(a: int, b: int, p: int) -> tuple[list[int], list[int]]:
    xlist, ylist = [], []
    for x, y in itertools.product(range(p), range(p)):
        if (x**3 + a*x + b - y**2) % p == 0:
            xlist.append(x)
            ylist.append(y)
    return xlist, ylist


def plot_ec(a, b, p) -> None:
    xlist, ylist = get_points(a, b, p)
    plt.figure(figsize=(5, 5))
    plt.axis([0, p, 0, p])
    if p < 55:
        point_style = 'o'
        plt.grid(which='major', linestyle=':', color='black')
        plt.yticks(list(range(p)))
        plt.xticks(list(range(p)))
    else:
        point_style = '.'
    plt.plot(xlist, ylist, point_style, color='black')
    plt.show()


plot_ec(1, 1, 17)

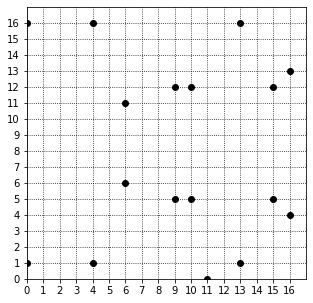
最早、見ただけでは楕円でもなければ曲線ですらないので分かりづらいですが、このような形で飛び飛びに様々な値をとっていることが分かると思います。

以下のようにパラメータの数を大きくしてみるとどうでしょうか。

plot_ec(0, 7, 977)

実際に暗号資産で使用されている $p$ はもっと巨大な数になりますが、イメージが湧いてきたかと思います。

楕円曲線暗号における鍵

楕円曲線暗号ではとある楕円曲線を定めると同時に、とある点Gをベースポイントとして定めます。例えば先ほどから具体例として挙げられるビットコインでは以下の楕円曲線とGを用いています。

楕円曲線

$\displaystyle y^2 \equiv x^3 + 7 \pmod {2^{256} - 2^{32} - 977}$

Gの座標

$\displaystyle G_x = 0x79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798$

$\displaystyle G_y = 0x483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8$

ここでとある整数 $k$ を定めます。これが秘密鍵となります。先ほどのRSA暗号では秘密鍵に素数を使うことしかできなかったため、どうしても巨大な数を取りうる必要があったのですが、楕円曲線を用いた暗号方式ではそのような制約がありません。なのでより小さなbit長で強固な鍵を作成することが可能です。またビットコインやイーサリアムで使用される上記の楕円曲線の位数は $2^{256}$ に近い値となっており秘密鍵はこの範囲内に存在していることになりますが、これは銀河系に存在してる原子数よりも多く、全宇宙に存在している原子数よりも少ないくらいであり、コンピューターを用いた計算でも総当たりで突き止めるにはあまりにも難しいことが分かります。この時以下のように $G$ を $k$ 倍して得られる点が公開鍵となります。

$\displaystyle K = kG$

$k$ から $K$ を求めることは先ほど説明した通り、非常に高速に行うことが可能です。（2倍、4倍、8倍,,,と繰り返せばOK）ただ逆に $K$ から $k$ を求めることは非常に困難を極めます。これを離散対数問題と言います。

RSA暗号では二つの巨大な素数、 $p$ と $q$ についてその積 $pq$ を求めることは容易だが、逆に $pq$ を素因数分解して $p$ と $q$ を見つけることが非常に困難でした。それを利用した暗号化でしたが、楕円曲線暗号でも同様に公開鍵から秘密鍵を特定することが困難です。

ECDH鍵共有

Elliptic curve Diffie–Hellman key exchange（楕円曲線ディフィー・ヘルマン鍵共有）は、事前の秘密の共有無しに、盗聴の可能性のある通信路を使って、暗号鍵の共有を可能にする公開鍵暗号方式の暗号プロトコルです。元々から存在していた、RSA暗号の仕組みを利用したディフィー・ヘルマン鍵共有を楕円曲線を使うように変更したものになります。

数式ベースでの手順説明

ECDHが暗号曲線を利用してどのように行われているのかについて解説していきます。以下の例を使います。

楕円曲線

$\displaystyle y^2 \equiv x^3 + x + 1 (\bmod 23)$

ベースポイント

$\displaystyle G = (4, 5)$

位数

$\displaystyle n = 19$

ここでAさんとBさんはそれぞれ公開鍵と秘密鍵を作成します。

Aさん
- 秘密鍵 $a=5$
- 公開鍵 $A=aG=(19, 20)$
Bさん
- 秘密鍵 $b=7$
- 公開鍵 $B=bG=(9, 7)$

AさんとBさんはお互いの公開鍵を交換します。そしてお互い共通鍵を作成します。必ず両者が一致する仕組みであることをうまく利用しています。

Aさん側（ $b$ の値を知らなくても良い）

$\displaystyle 共通鍵K = aB = abG = (2, 3)$

Bさん側（ $a$ の値を知らなくても良い）

$\displaystyle 共通鍵K = bA = baG = (2, 3)$

これで第三者にバレることなく共通鍵を共有することができました。ここから先の流れですが、お互いの共通鍵における $x$ 座標からAES-256鍵を作成し、それを使って暗号化と復号を行うことになります。実にシンプルかつ強固な仕組みです。

コードベースでの手順説明

ここでPythonを使ってECDH鍵交換を実装してみます。まず、お互いの公開鍵と自身の秘密鍵から共有鍵の作成を行う流れです。

from cryptography.hazmat.primitives.asymmetric import ec
from cryptography.hazmat.primitives.kdf.hkdf import HKDF
from cryptography.hazmat.primitives import hashes
from cryptography.hazmat.backends import default_backend


# 鍵ペアを生成 (Alice)
private_key_alice = ec.generate_private_key(ec.SECP256R1(), default_backend())
public_key_alice = private_key_alice.public_key()

# 鍵ペアを生成 (Bob)
private_key_bob = ec.generate_private_key(ec.SECP256R1(), default_backend())
public_key_bob = private_key_bob.public_key()

# 共有秘密鍵を計算 (Alice)
shared_key_alice = private_key_alice.exchange(ec.ECDH(), public_key_bob)

# 共有秘密鍵を計算 (Bob)
shared_key_bob = private_key_bob.exchange(ec.ECDH(), public_key_alice)

# 共有秘密鍵が一致することを確認
assert shared_key_alice == shared_key_bob   # OK

次にこの共有鍵から暗号化・復号を行う流れです。

import os
from cryptography.hazmat.primitives.ciphers import Cipher, algorithms, modes


def derive_key_and_iv(shared_secret, salt, info=None):
    """ 鍵導出関数 (HKDF) を使って共有秘密鍵から暗号化鍵とIVを生成
    """
    if info is None:
        info = b''
        
    hkdf = HKDF(
        algorithm=hashes.SHA256(),
        length=32 + 12,  # 32 bytes for the AES key, 12 bytes for the IV
        salt=salt,
        info=info,
        backend=default_backend()
    )

    key_and_iv = hkdf.derive(shared_secret)
    return key_and_iv[:32], key_and_iv[32:]


def encrypt(plaintext, key, iv):
    """
    共通鍵と初期化ベクトルから暗号化を行う
    """
    cipher = Cipher(algorithms.AES(key), modes.GCM(iv), backend=default_backend())
    encryptor = cipher.encryptor()
    ciphertext = encryptor.update(plaintext) + encryptor.finalize()
    return (ciphertext, encryptor.tag)


def decrypt(ciphertext, key, iv, tag):
    """
    共通鍵と初期化ベクトル、及び暗号化の際に生成されたタグ情報から復号を行う
    """
    cipher = Cipher(algorithms.AES(key), modes.GCM(iv, tag), backend=default_backend())
    decryptor = cipher.decryptor()
    return decryptor.update(ciphertext) + decryptor.finalize()


# 両者で共有するsaltを生成
salt = os.urandom(16)
# Alice が鍵と IV を生成
key_alice, iv_alice = derive_key_and_iv(shared_key_alice, salt=salt)
# Bob が鍵と IV を生成
key_bob, iv_bob = derive_key_and_iv(shared_key_bob, salt=salt)

# 共有鍵が一致することを確認
assert key_alice == key_bob
assert iv_alice == iv_bob

# 暗号化と復号の例
plaintext = 'WBC2023 大谷翔平とマイク・トラウトの夢の対決が実現'
plaintext = bytes(plaintext.encode('utf-8'))

# Alice が平文を暗号化
ciphertext, tag = encrypt(plaintext, key_alice, iv_alice)

# Bob が暗号文を復号
decrypted_text = decrypt(ciphertext, key_bob, iv_bob, tag)

# 復号されたテキストが元の平文と一致することを確認
assert decrypted_text == plaintext

print(f'Original plaintext: {plaintext.decode("utf-8")}')
print(f'Encrypted ciphertext: {ciphertext}')
print(f'Decrypted plaintext: {decrypted_text.decode("utf-8")}')

Original plaintext: WBC2023 大谷翔平とマイク・トラウトの夢の対決が実現
Encrypted ciphertext: b'5\xf5\x83J\x89\xaeyAn\xf1\xbc\xc5\xb9\xe1\xfd{L\x99w\x92\x11\xd3\xc1G\x84&:\x98\xe6\x1b\xb6\xc32\x83C\x1bK\xd0\xee\x97X#\xcc\xcc\\:\xa6\x84d\xe3(\xfa\x16\r\xf6\x08\xde\x1f\xa9\x99\xf5g)T\xf0O>\xcb\x11f\x8f'
Decrypted plaintext: WBC2023 大谷翔平とマイク・トラウトの夢の対決が実現

尚、暗号化の途中で初期化ベクトル（IV）やタグなどの変数が使われていますが、今回は共通鍵暗号方式に関する説明を一旦省略させてもらいます。簡単に概要だけ述べると暗号化を行う際にランダム要素を加えることでよりセキュアな通信を行うための工夫です。

（補足）今回は既存のライブラリを使って鍵交換を行いましたが、参考文献にて紹介するプログラミング・ビットコインでは自身で楕円曲線クラスを実装していくところから学べるので、非常に勉強になると思います。

ECDSA署名

楕円曲線を利用した暗号としてもう一つ有名なECDSA署名についても解説します。なおこの章では先ほどのまでのように具体的な数字を入れて解説するのも再掲になってしまう部分が多いため、コードベースの解説にさせてください。

電子署名とは？

ECDSAについて解説する前に電子署名について軽く触れておきます。今更感ある人はスルーしてください。

アリスさんはボブさんに対してメッセージを送りたい
アリスさんは第三者によるなりすましを防ぎたい
また、アリスさんは第三者によって文書改ざんが行われた際にそれがわかるようにしておきたい
そこでボブさんに対してメッセージ本文とは別に署名を送付する
この署名はアリスさんの秘密鍵と実際のメッセージ本文から生成されるもの
ボブさんは受け取ったメッセージと署名と、事前に持っているアリスさんの公開鍵を使用して次の2点を検証する
メッセージがアリスさんから送付されたものであるか
メッセージが改ざんされていないかどうか

箇条書きでつらつらと書いていきたましたが、Google画像検索なでしてイラストベースで確認した方が理解しやすいかもしれません。

数式ベースでの手順説明

まず、メッセージの送信側（署名をする側）は公開鍵 $Q$ と秘密鍵 $d$ を用意します。 $G$ は先ほどまでと同様、ベースポイントを表します。

楕円曲線

$\displaystyle y^2 = x^3 + ax + b \pmod p$

楕円曲線の位数

$\displaystyle n$

秘密鍵

$\displaystyle d$

公開鍵

$\displaystyle Q = dG$

次にメッセージ $m$ をハッシュ化しとある数値情報 $H(m)$ に変換します。そしてランダムな整数 $k$ を用意し、署名用の一時的な公開鍵 $K$ を計算します。ここでは深く述べませんが、乱数 $k$ の生成も通常の秘密鍵同様、漏れてはいけない情報になります。割と有名な話だと思いますが、PlyaStation3で実際に起こったソフトウェア署名鍵漏洩問題は、この乱数 $k$ を固定値として実装してしまったことが原因らしいです。

$\displaystyle K = kG$

この時、生成された一時的な公開鍵 $K$ の $x$ 座標を $K_x$ とします。あとは以下の様に $r$ と $s$ を計算し、その組み合わせを書名とします。送信側はトランザクションとともに、この電子署名、および元々の公開鍵 $Q$ と一時的な公開鍵 $K$ を受信側に送ります。

$\displaystyle \begin{eqnarray} r &=& K_x \\ s &=& k^{-1} * \bigl( H(m) + d * r \bigr) \\ \end{eqnarray}$

生成された署名：

$\displaystyle (r, s)$

メッセージの受信側ですが、まず受け取ったメッセージ $m$ をハッシュ化し $H(m)$ を得ます。次に署名要素 $(r, s)$ と公開鍵 $Q$ を使って以下の値 $K'$ を計算します。

$\displaystyle K' = \dfrac{H(m)}{s} * G + \dfrac{r}{s} * Q$

この時得られた $K'$ と一時的な公開鍵 $K$ の $x$ 座標が一致した時、署名の検証が完了します。

$\displaystyle K_x = K'_x$

検証プロセスの証明

以下、証明です。

$\displaystyle \begin{eqnarray} K' &=& \dfrac{H(m)}{s} * G + \dfrac{r}{s} * Q \\ &=& \dfrac{H(m)}{s} * G + \dfrac{r}{s} * dG \\ &=& \biggl( \dfrac{H(m)}{s} + \dfrac{r}{s} * d \biggr) G \\ &=& \biggl( \dfrac{H(m) + dr}{s} \biggr) G \\ \end{eqnarray}$