はじめに

このブログに書かれていること

前半
- 古代暗号から始まる暗号の歴史
- エニグマの構造と解読法について
後半（後半ブログはこちら）
- RSA暗号の基本
- 楕円曲線暗号の基本

自己紹介

こんにちは！株式会社ABEJAの @Takayoshi_ma です。今回のテックブログですが、ネタに5時間程度悩んだ挙句、暗号を取り上げることにしました！暗号化手法の解説にとどまらず、その歴史なども簡単に紹介しています。それなりのボリュームになってしまいましたが、エンタメとして読んでいってくれると幸いです。今回のブログでは前半のエニグマまで進めていきます。

注意

本ブログで書かれているサンプルコードのセキュリティ強度は保証できません。あくまでも例として書いているだけなのでご注意ください。

Part1 古典暗号

2つの暗号方式

早速暗号の歴史に入る前に、前提として以下の2つの暗号方式について言葉の定義を確認します。

key	value
転置式（てんちしき）暗号方式	文字の順番を並び替える
換字式（かえじしき）暗号方式	別の文字に置き換える

これ以降、換字式暗号がこのブログにテーマになってきますが、最初に一つだけ転置式暗号の例を取り上げていきたいと思います。

スキュタレー暗号

※ 画像はStable Diffusionより生成

紀元前６世紀頃、古代ギリシャの都市国家スパルタで用いられていた暗号です。あらかじめ決まった太さの棒を暗号の送信元と受信先で共有します。これが鍵になります。アルゴリズム自体は至ってシンプルであり、暗号文の送り手がその棒に革紐を巻きつけて棒に沿って文字を書き、その革紐だけを受け手に送るというものです。受けとった側が同じ太さの棒（鍵）を持っていないとバラバラに並んだ文字を読み解くことができないという仕組みになっています。

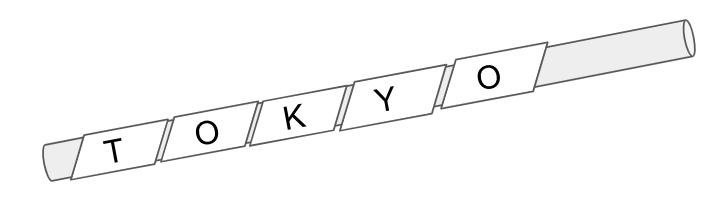
アルゴリズムと鍵

スキュタレー暗号は非常にシンプルです。個人的なイメージですが、脱出ゲームなどでよく出てきそうだなと思います。しかしながらこの古代暗号の時代から既に暗号というものの本質が見え隠れしていると言っても過言ではありません。暗号の本質、それはアルゴリズムと鍵です。

アルゴリズム
- 文章を暗号化および復号（暗号を解いて読むこと）する際のルール、または手順
鍵
- アルゴリズムと共に使用されるデータの暗号化と復号に関する情報の一部

以降、沢山の暗号が出てきますが、もれなくこの2つの組み合わせで暗号は成り立っています。また後述にはなりますが、時代を経るごとに暗号は「アルゴリズムを如何に工夫するか」よりも、「鍵をどうやって強固にするのか」という視点に変わっていきます。

シーザー暗号

原理

いわゆるシフト暗号です。紀元前１世紀頃、ユリウス・カエサル（英：ジュリウス・シーザー）が頻繁に利用したと言われています。以下はひらがなを３文字ずつシフトした例です。

平文：　あい（1 2）

暗号文：　えお（4 5）

そのままシフトするだけだと例えばアルファベットの場合、26パターンを試せば簡単に解読できてしまいます。しかし、均等にずらすのではなく、以下の例のようにランダムに換字しても良いということにすると、そのパターンは実に $26!$ 通り（403291461126605635584000000パターン）もの膨大な数になります。これら全てのパターンを全探索する場合、現代のコンピューターを持ってしても無謀な数字であることが想像できると思います。

頻度分析

ではコンピュータもない時代に、どうやってこの暗号は突破されていったのでしょうか？それが頻度分析と呼ばれる手法です。例えば英語には以下ような特徴があります。

"e"という文字が最も多く使われる傾向がある
"q"の後は必ず"u"がくる
any, and, the, are, of, if, is, it, in の単語の頻出度が高い
"ing", "ed"などが語尾に来ることが多い

このように、言語特有の事情を考慮することで鍵を推測していく手法になります。ある程度長い文章にしか使えない手法ですが、シンプルな換字暗号に対する一つの答えになります。また、この手法は言語の特徴を捉えていないと法則を見つけ出せないことから、当時の暗号解読は数学者よりも言語学者が取り組むことが多かったようです。

アルベルティ暗号ヴィジュネル暗号

この2つの暗号は本質的に同じものとなるため一緒に紹介します。アルベルティ暗号ですが、端的に表現すると「１文字ごとに異なる鍵を交互で使用する換字暗号」になります。例を挙げていきます。以下の2つの鍵が存在するとします。

鍵１	鍵２

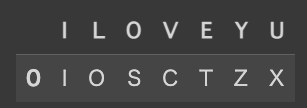そして以下の文字列を暗号化したいとします。

I LOVE YOU

この時テキストの奇数番目には鍵１を偶数番目には鍵２を使用すると以下のような暗号文になるかと思います。

平文：　ILOVEYOU

暗号文：　SORCZZRX

このように複数の鍵を使い分けることで、例えば換字後の文字Zを見たときに、元の文字がEだったりYだったりしていることが分かります。このアルベルティ暗号を一般化したものがヴィジュネル暗号です。先ほどは2つの鍵を交互に分けて使っていましたが、ヴィジュネル暗号は代わりに鍵となる特定の単語を決めます。例えば特定の単語をAPPLEとします。この時、以下のような形で暗号化していきます。（復号はその逆をすればOK）

1文字目のIに対して鍵Aを使って換字します
２文字目のLに対して鍵Pを使って換字します
３文字目のOに対して鍵Pを使って換字します
４文字目のVに対して鍵Lを使って換字します
５文字目のEに対して鍵Eを使って換字します
６文字目のYに対して鍵Aを使って換字します
７文字目のOに対して鍵Pを使って換字します
８文字目のUに対して鍵Pを使って換字します

以下のマトリックスを例に取り上げます。このマトリックスに特定の単語を組み合わせることで複雑な鍵を実現しています。例えば、1文字目のIに対して鍵Aを使って換字した場合、方陣のA行I列を元にYへ換字されます。

如何にしてヴィジュネル暗号は破られたか

ヴィスネル暗号はその複雑性から長年解読が不可能とされていました。しかし19世紀のイギリスで、コンピュータの父とも呼ばれる数学者のチャールズ・バベッジによって、破られます。バベッジはヴィジュネル暗号の周期性に着目します。例えば鍵２としてUSAというワードを選択した場合、'the'という英単語は、上記のヴィジュネル方陣を使うと、以下のいずれかのパターンに暗号化されることがわかると思います。

CXQ
ZNA
NSE

'the'という文字列が頻繁に平文に出現する場合、以上の文字列も同様に出現するものと考えられます。そうすると1/3の確率でどれかに変換されますが、例えば今300, 90, 30, 333文字おきにCXQというワードが現れたとします。その場合４つの数字の公約数のいずれかが、鍵の長さである可能性が高そうだと推測できると思います。実際今回の鍵長は3なので、この周期で同じワードが現れることはあり得る話です。このように同じ文字が周期的に現れているかをチェックし、あり得そうな鍵長をいくつか推定します。その後、その周期ごとに文字を抽出し、頻度推定にかけていけばいずれ暗号解読につながるというわけです。このように同じ文字が周期的に現れているかをチェックし、あり得そうな鍵長をいくつか推定します。その後、その周期ごとに文字を抽出し、頻度推定にかけていけばいずれ暗号解読につながるというわけです。

Part2 近代暗号

エニグマ

エニグマの登場

暗号について話す際、度々話題に挙がるのがエニグマだと思います。第二次世界大戦中のドイツで考案されたエニグマですが、強固なセキュリティであることはもちろん、暗号化・復号の作業が非常に簡易であり、素早くできるという特徴があります。

エニグマ本体	使用された歯車

※ 画像はWikipediaより抜粋：https://ja.wikipedia.org/wiki/%E3%82%A8%E3%83%8B%E3%82%B0%E3%83%9E_(%E6%9A%97%E5%8F%B7%E6%A9%9F)

エニグマの写真を見てみるとタイプライターのような構造をしていますが、平文をタイピングすることで暗号化後の文字列を即時に得ることが可能です。（正確にはランプボードに換字後の文字が点灯する）一方、暗号化された文字列をタイピングすることで復号後の平文を取得することが可能です。

エニグマは時を経るごとにバージョンアップされていき、少しずつその鍵も複雑化されていきますが、基本原理はヴィジュネル暗号と変わりません。ただ通常のヴィジュネル暗号よりも

暗号化・復号の手間を簡単にする
膨大な鍵を使用する

という点で非常に画期的です。しかし、解読困難とされたエニグマはやがてイギリスの数学者であり、チューリングマシンやチューリングテストなどで有名なコンピュータ科学の父、アラン・チューリングによって突破されてしまいます。因みにこの暗号の解読は第二次世界大戦の終結を二年間は早めたと呼ばれるほどの功績とされているようです。気になる方は映画『イミテーション・ゲーム／エニグマと天才数学者の秘密』をご覧ください。僕も観ました。

エニグマの基本構造

機械工学的な視点を省いて、エニグマの構造をシンプルな例で解説していきます。以下、3つのスクランブラー（ローター）と1つのリフレクターが存在します。ローターの役割はシンプルで、ある文字をある文字に変換する、いわゆる換字を行う回路です。リフレクターは入力された電気信号を反射して直前のスクランブラーに返す回路です。尚、本当はプラグインと呼ばれる回路も存在しますが、文字のスワップを行うだけなので、一旦説明からは割愛します。

本当は文字の数（アルファベットなら26）だけ必要なのですが、簡略化してI, L, O, V, E, Y, Uの7文字しかないと仮定して図示しています。この場合、例えばLという文字をタイプするとUという文字に暗号化されることが分かります。

そして、ここからがエニグマの画期的な点ですが、暗号後の文字Uをタイピングすると元のLが得られることが分かります。

つまり、暗号化の際はタイピングして出てきた文を送るだけ、復号の際は送られてきた文字をタイピングして元に戻すだけ。という使い勝手の良さを達成していることになります。

ただ、ここで

「こんなシンプルな換字ならシーザー暗号と変わらないじゃないか」

という疑問が出てきます。エニグマはこの問題に対して、ローターに工夫を加えることで、対処しています。

例えば、上のエニグマ機構に対してローター１を下図のように一つずらした状態で、もう一度Lの文字を暗号化してみます。すると今後はVの文字が得られることが分かります。

つまり、この場合ローターの数が3つ、それぞれの換字パターン7つを合わせ、以下のパターンだけ鍵が存在することが分かります。

$\displaystyle 7 ^ 3 = 343$

上記の例だと少ないように感じますが例えば、使われる文字数が26個、セットされるローターの数が3、さらに合計6個のローター（付け替え可能）の中から3個を選んで使うとなると以下の数だけ鍵が存在することが分かります。

$\displaystyle 26 ^ 3 × {}_6 P_3 = 2109120$

ドイツ軍はこのエニグマを以下のように運用していたとされています。

ローター１が１周するごとにローター２を1つシフトさせる
- 要は時計の秒針と分針のイメージ
ローター２が１周するごとにローター３を1つシフトさせる
- 要は時計の分針と時針のイメージ
プラグインに工夫を施すことで、換字のバリエーションを増やしていた
- 具体的には変換後文字のスワップを多数行なっていた
エニグマに使われるローターの種類や、初期設定をデイリー変更（リセット）するこれを日鍵という
実際に暗号化に使用するメッセージ鍵はこの日鍵と違うものを使用する
- 最初のメッセージでメッセージ鍵を日鍵で暗号化して送信した上で、メッセージ鍵を互いに共有していた
日々の日鍵が定められたコードブックを軍の中で共有する
- コードブックを月一で新調する
終戦末期にはセット可能なローターの数を増やすなどしていた

如何にしてエニグマは突破されたか

前提条件

前述の通りエニグマは連合国軍によって、解読されてしまいました。シンプルに全探索をしているだけでは、突破できそうに無いエニグマですがどのような経緯で破られてしまったのでしょうか。その説明の前に、以下の前提条件があったことを先に列挙しておきます。

チューリングは暗号解読に機械の計算力を利用した
エニグマ本体や、使われていたスクランブラーなどの実機を連合国軍は既に入手していた
- なのでスクランブラーやプラグインの初期設定がどのようにセッティングされていたのかを知るだけでよかった。
エニグマでは、同じ文字に暗号化されることがない
平文の冒頭付近に特定の文字列が多用されていた
- 例）午前６時過ぎに天候を伝えるメッセージと、ヒトラーを讃えるセンテンスなど

3つ目に関してですが、リフレクターの性質上エニグマではAが暗号化されてBになるとき、Bを暗号化してできる文字は必ずAになるという特性があります。さらに、AがAに暗号化されることがなく、必ず異なる文字に暗号化されるという特徴があります。上図では文字数が奇数になってしまってるので例が悪いのですが、L <-> V、I <-> Y、E<-> U、O <-> Oがそれぞれセットになっていることが分かります。文字数が偶数の場合、どれか一つ対になる文字が存在するので、必ず違う文字に変換される仕様です。チューリングはこの点に着目しました。

必ず異なる文字に変換される性質を利用

例えば、平文に天候を表す文章、wetternullsechsが必ず含まれていると仮定します。尚、このように元の平文に必ず含まれているセンテンスや単語をクリブと呼びます。まずはこのクリブが暗号文中のどの辺りに存在しているか、可能な限り、絞り込む必要があります。ここで『必ず異なる文字に変換される』ことから以下の暗号文から平文に変換することは不可能であることが分かります。なぜならばwetterのeが暗号文の4文字目と同じEに変換されることはあり得ないからです。

暗号文：IPRENLWKMJJSXCPLEJWQ

元平文：（先頭二文字）wetternullsechs

ここで、右に1つした場合はどうでしょうか？この場合、暗号文のように変換される可能性はあります。このような形でクリブが暗号文のどの箇所に存在するのかを推測していきました。

ループを利用

先ほど、暗号解読に機械を利用したと述べましたが、どのような手法を用いたのか解説していきます。ここでは例として、天候を表すドイツ語wetterを取り上げます。この平文がETJWPXという暗号文に変換されていたと仮定します。そうすると以下のように w → E → e → T → t → W（先頭文字） というループが存在していることが分かります。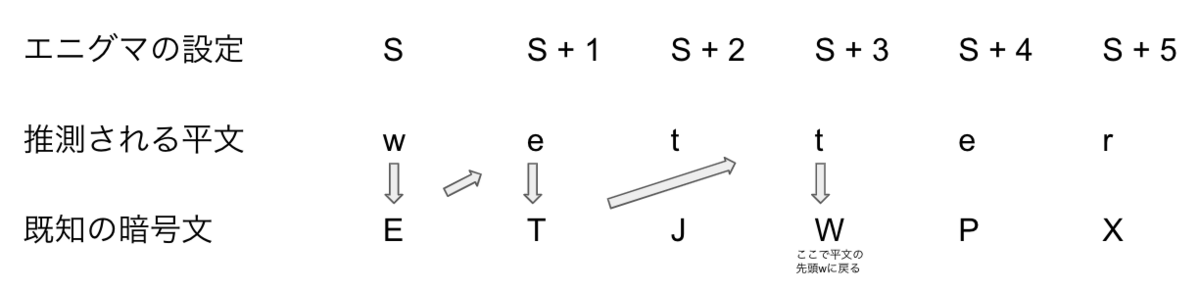さらにここが肝なのですが、チューリングは以下のように仮想エニグマを三台直列に並べ電気回路を作りました。ここで大切なのは2つ目のエニグマの鍵を１つ目のエニグマの鍵設定から $+1$ 、3つ目の鍵を $+3$ ずつずらしていることです。この設定の状態で先頭のエニグマの鍵を高速で全探索していきますが、その時2つ目のエニグマも3つ目のエニグマもそれぞれ、 $+1$ 、 $+3$ ずつ鍵がずれた状態で動いていくことになります。この設定の状態で先頭のエニグマの鍵を全探索していくと2つ目のエニグマも3つ目のエニグマを1つずつ鍵がずらされていくことになります。そして探索の結果、正しい設定にたどり着いた際、以下の電気回路に正しく電流が流れることが分かります。後は、正しいと思われる鍵を使って元々の暗号文を平文化します。プラグボードの設定でいくつかの文字がスワップされているため、おかしな平文が出てくるかと思いますが、そこから先は見た目の違和感でいくつかの文字を交換するだけなので、手作業でも解読が可能です。

まとめ

長くなりましたが、エニグマ解読の手順をまとめると、以下のような流れです。

使えそうなクリブを列挙する
それらのクリブが暗号文のどの箇所に出現するのかを見極める
- 冒頭に出てくることが多かった
- 同じ文字に暗号化されることがない性質を上手く利用した
ターゲットとなるクリブと暗号文の箇所を決めたら、ループが発生しているかどうかを確認する
エニグマ３台を直列に繋いだ回路を用意した
- そのとき2台目と3台目はクリフと暗号文のループを利用して指定の数だけずらしておいた。
- ローターの設定が例えば前述の ${}_6 P_3$ 通りあった場合、それらは並列に用意して同時に検証することが可能であることもポイント
機械の力を利用して、高速にシミュレーションした
正しいと思われるローターの設定がわかった後、プラグインの設定がどうなっているかを手作業で解読した

特にスマートな点はプラグインの検証とローターの検証を分離して行えることに気づいた点だと思います。その工夫によって探索の幅を極端に少なくしていることが分かるかと思います。

後半パートへ続く

参考文献

www.oreilly.co.jp

www.shinchosha.co.jp

manabitimes.jp

採用情報

ABEJAでは共に働く仲間を募集しています。気になった方は是非ご連絡ください。

careers.abejainc.com

ABEJA Tech Blog

中の人の興味のある情報を発信していきます

暗号の歴史と現代暗号の基礎理論（RSA, 楕円曲線）-前半-