はじめに

こんにちは！ABEJAでプロダクトマネージャーをしている栗林です！ ABEJAでは小売店舗での顧客行動を分析するInsight for Retailというプロダクトや、オフィスDX事業をはじめとして、物理世界の現象を機械学習などが適用可能なデジタルに変換する部分にも強みがあります！本日のTech Blogでは、安価かつ小型な加速度・角速度センサーを用いて製造業や物流業における作業者の行動や状態を推定する手法についてまとめました。

背景

みなさんは製造業や物流などにおける、正味作業時間という言葉をご存知でしょうか？正味作業時間とは実際の作業に充てられた時間を差します。例えば、組み立て作業の際に必要となる道具や在庫が近くに無く、作業者がものを探したり歩行して取りに行ったとします。このときの準備や段取りにかかる時間は準備時間や付帯作業時間と言われ、作業工程において生産をおこなえていない状態となっています。少しでも生産効率の向上を目指す現場においては、生産活動が行えていない時間をなるべく短くするためレイアウトの工夫や無駄な作業の省略など改善を行う必要があります。

しかしながら、多くの現場では改善の基礎的な情報となる生産効率を常時計測する方法がありません。作業日報を使って人の手で記録をするか、万歩計によって人ごとの移動時間や距離を計測するなどの方法もありますが、正確さに欠けるうえ情報の解像度も十分に高いとは言えません。そんななか、昨今ではBLE（ビーコン）やWi-Fiを使い移動時間だけでなく位置も計測する方法が登場しました。これらは親機（基地局の役割）となる電波の発信元と子機となる作業者側のタグ（可搬型の端末）を用いることで電波強度や位相からその位置を推定することができるのです。このような、正確に計測可能なBLEやWi-Fiではなくより安価に作業時間を計測できる方法として加速度・角速度センサーを用いる方法があります。

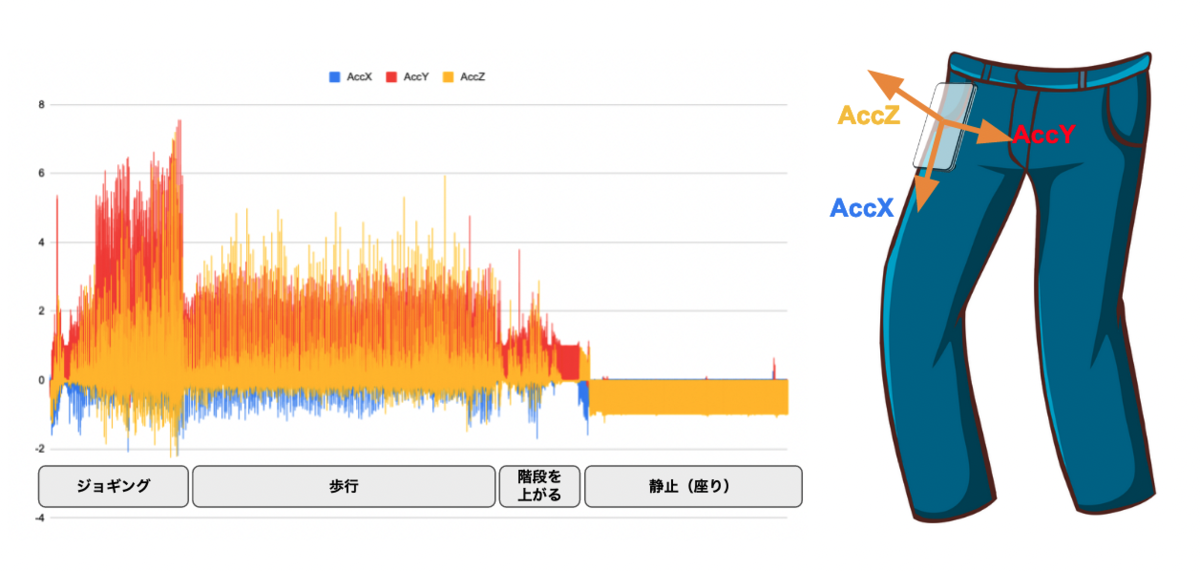
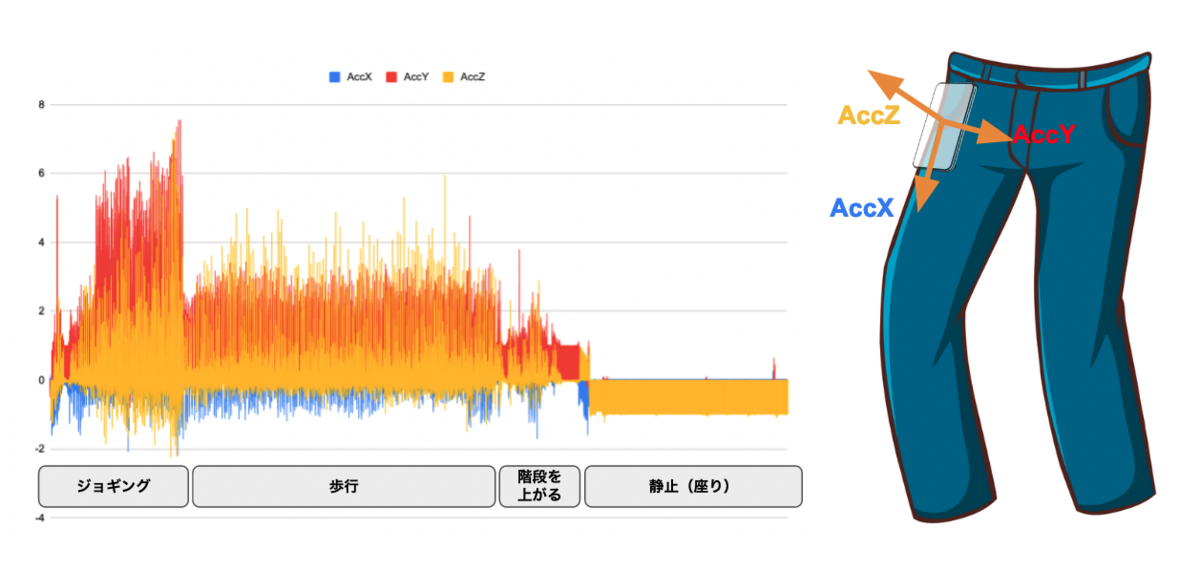
下記は加速度センサーから取得した歩行や静止中の加速度情報です。それぞれの行動ごとに違いがあることがわかります。

問題設定

今回解きたい問題として、作業者を想定した人間の歩行時間、立ち止まり静止時間、座り静止時間を分類することとします。また、適用したい場所の広さや形状に寄らず使用できるよう、作業者側にとりつけたセンサから取得できる情報のみを扱います。

データ

人間の歩行や静止時の加速度・角速度をもとにしたデータセットしては下記のものがあり、こちらをもとに行動の分類を行い、実際にセンサーによって計測したデータの分類を試します。

github.com

データセットでは、センサー（iPhone）はポケットの中に入れた状態を仮定します。歩行時には歩行による加速度や角度変化が発生し、立ち止まっているときと座っているときではポケットの中のスマートフォンの角度が違っていると考えられます。

準備

センサー

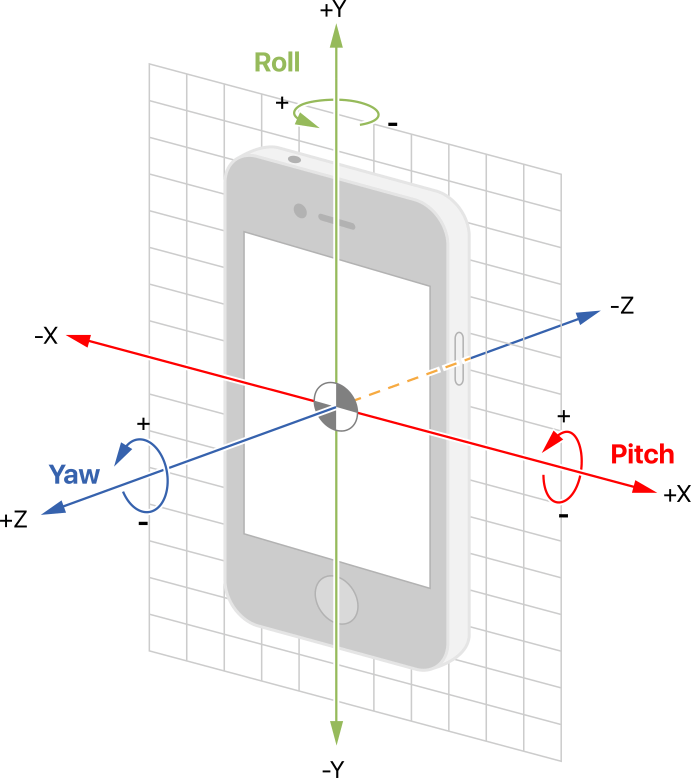
加速度と角速度を計測するためのセンサーは二つセットになったものもあり、X・Y・Zの3軸方向それぞれの加速度と角速度を計測できることから6軸センサーなどとも呼ばれます。 amzn.to

センサー情報を取得し、SDカードなどに蓄積するためにマイコン等を用いることも考えましたが今回はそれらの機能がパッケージ化されたM5stackを使います。 M5Stackは、約5cm×5cmの正方形のケースの中にWi-FiとBluetoothによる無線通信機能を備えたCPU（ESP32）をはじめ、カラー液晶ディスプレイ・プッシュボタン・スピーカ・microSDカードスロット・バッテリーなどの周辺部品がひとつのモジュールにまとまっている、小型のマイコンモジュールです。IoT機器を開発する際によく使われる機能がパッケージ化されているため、配線の必要がなく簡単に使うことができます。

amzn.to

ロギング

M5Stackのセンサー情報を取得するスクリプトを作成します。今回は6軸センサが実装されているｍ5Stack core2を購入したのですが、どこかで見たことのあるようなコンソールが表示されました。

加速度と角速度のRawデータ、それらから計算した姿勢角度データを同時にcsvに保存できるように処理を行います。

#define M5STACK_MPU6886

#include <M5Stack.h>

File file;

float accX, accY, accZ;
float gyrX, gyrY, gyrZ;
float pitch, roll, yaw;
float temp_pitch, temp_roll, temp_yaw;

int Xdot[320];
int Ydot[320];
int Zdot[320];
float range_table[5] ={ 1.0 , 2.5 , 5.0 , 0.25 , 0.5 };
float range_tableAcc[5] ={ 1.0 , 2.5 , 5.0 , 10.0 , 15.0 };
int range = 0;
unsigned long PreviosTime = 0;

void setup(){
  M5.begin();
  M5.Power.begin();
  M5.IMU.Init();
  M5.Lcd.fillScreen(BLACK);
  M5.Lcd.setTextColor(GREEN , BLACK);
  M5.Lcd.setTextSize(1);

  PreviosTime = millis();

  SPI2.begin(0, 36, 26, -1); // SPI初期化
  if(!SD.begin(-1, SPI2)) { // SDカード初期化
  M5.Lcd.println("Card Mount Failed");
  return;
}

void loop() {

  int x = 0;
  static char sel = '\0';

  if( (millis() - PreviosTime ) >= 100 ){
    PreviosTime = millis();
    sel = check_button_status();
  }

  // 3軸角速度
  M5.IMU.getGyroData(&gyrX,&gyrY,&gyrZ);
  M5.Lcd.setCursor(0, 0);
  M5.Lcd.printf("gyro=(%5.1f, %5.1f, %5.1f)", gyrX, gyrY, gyrZ);

  // 3軸加速度
  M5.IMU.getAccelData(&accX,&accY,&accZ);
  M5.Lcd.setCursor(0, 50);
  M5.Lcd.printf("acc=(%5.1f, %5.1f, %5.1f)", accX, accY, accZ);
  
  M5.IMU.getAhrsData(&pitch,&roll,&yaw);
  M5.Lcd.setCursor(0, 100);
  M5.Lcd.printf("PRY=(%5.1f, %5.1f, %5.1f)", pitch, roll, yaw);

  // 姿勢角
  float my_roll = atan(accY / accZ) * RAD_TO_DEG;
  float my_pitch = atan(-accX / sqrtf(accY*accY + accZ*accZ));
  M5.Lcd.setCursor(0, 150);
  M5.Lcd.printf("pitch = %5.1f, roll = %5.1f", my_pitch, my_roll);
  
  file = SD.open("/logger.csv", FILE_WRITE);
  file.println((String)accX + "," + (String)accY + "," + (String)accZ "," + (String)gyrX + "," + (String)gyrY + "," + (String)gyrZ "," + (String)roll + "," + (String)pitch + "," + (String)yaw);

  switch(sel){¥
    case 'A': // 3軸角速度
              Xdot[319] = gyrX * range_table[range];
              Ydot[319] = gyrY * range_table[range];
              Zdot[319] = gyrZ * range_table[range];
              M5.Lcd.setCursor(0, 220);
              M5.Lcd.printf("[Gyr] [x%4.2f]",range_table[range]);           
              break;
    case 'B': // 3軸重力加速度
              Xdot[319] = accX * range_tableAcc[range];
              Ydot[319] = accY * range_tableAcc[range];
              Zdot[319] = accZ * range_tableAcc[range];
              M5.Lcd.setCursor(0, 220);
              M5.Lcd.printf("[Acc] [x%4.2f]",range_tableAcc[range]);          
              break;              
    case 'C': // 姿勢角
              Xdot[319] = pitch * range_table[range];
              Ydot[319] = roll * range_table[range];
              Zdot[319] = yaw * range_table[range];
              M5.Lcd.setCursor(0, 220);
              M5.Lcd.printf("[Attitude] [x%4.2f]",range_table[range]);         
              break;  
    default:
              Xdot[319] = gyrX * range_table[range];
              Ydot[319] = gyrY * range_table[range];
              Zdot[319] = gyrZ * range_table[range];
              M5.Lcd.setCursor(0, 220);
              M5.Lcd.printf("[Gyr] [x%4.2f]",range_table[range]);           
              break;      
  }
}


char check_button_status(void)
{
  static char previous_button = 'A';
  char current_button = '\0';
  int x;
  
  M5.update();              // update button state
  
  if (M5.BtnA.isPressed()) {
    current_button = 'A';
  }
  if (M5.BtnB.isPressed()) {
    current_button = 'B';
  }
  if (M5.BtnC.isPressed()) {
    current_button = 'C';
  }

  if(current_button != '\0'){
    if(previous_button == current_button){
      range++;
      if(range >= 5){
        range = 0; 
      }
    }
    if(previous_button != current_button){
#if 0
      for( x = 0 ; x <=318 ; x++ ){
        Xdot[x] = 0;
        Ydot[x] = 0;
        Zdot[x] = 0;
      }
      M5.Lcd.fillScreen(BLACK);
#endif
      previous_button = current_button;
      range = 0;
    }
  }
  return previous_button;
}

（こちらの記事を参考にさせていただきました）

分析

ロギングし歩行時の姿勢角と加速度をプロットしたものが下記です。

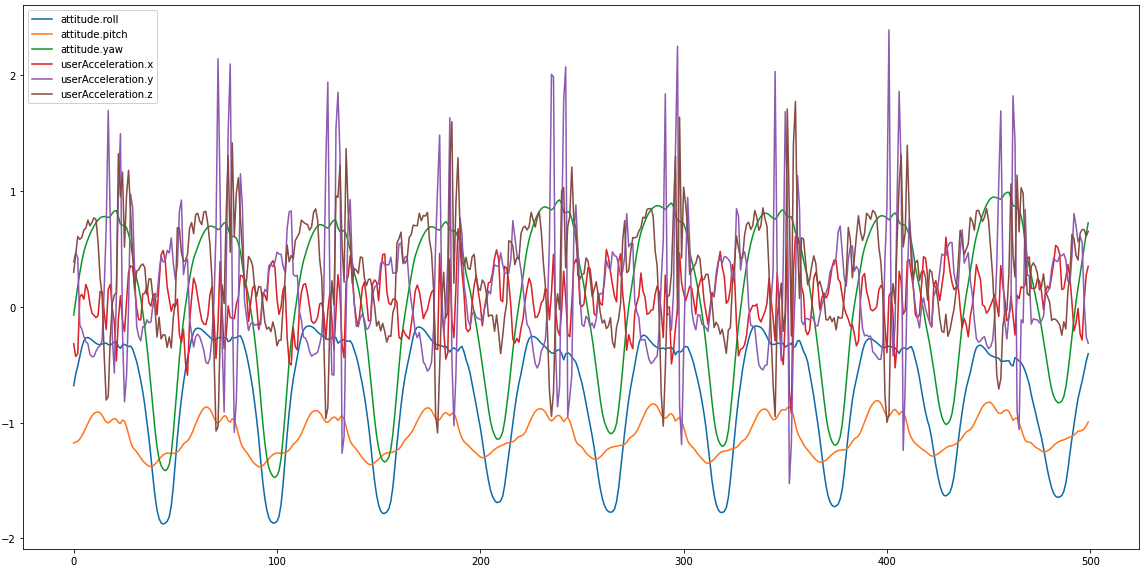
次に立ち止まり時のプロットです。

加速度は[m/s²]、角度は[rad]で簡易に表示していますが、上記を見比べても歩行時と静止時で差がありそうなことがわかります。また、歩行時のデータから特定の周波数で歩行による振動が発生していることがわかります。歩行速度が速い（ジョギング）の際にはこの周波数は高くなりそうです。

分析の方針

当初の予定では、簡易に歩行か否かの分類が行えればよいと考えておりFFT（高速フーリエ変換）で、特定の周波数帯域における振動を歩行状態とみなすことなどを考えていました。しかし取り扱うデータセットでは、ユーザーに対してセンサーの取り付けが厳密に同じでないことから、特定の軸方向に対して必ずしも同じ周波数や振動数であるわけではないことがわかりました。そこで機械学習によって分類を行うことにしました。

Apple Developer Documentation

同様のデータセットを使用した事例[1]があり、そちらを参考にしながら分析をすすめました。データセットでは以下の6つのラベルに紐づくセンサーデータがまとめられています。

0 : 　dws  :  階下へ降りる
1 : 　ups  :  上の階へ昇る
2 : 　wlk  :  歩く
3 : 　jog   : ジョギング
4 : 　std   :  立っている
5 : 　sit    :  座っている

特徴量

加速度センサーデータと角速度センサーデータから特徴量を計算します。モデルに学習させる特徴量として次のものを選定しています。

median: 中央値
std: 標準偏差
amplitude: 振幅
frequency: 周波数
phase: 位相

データ区間長さは先ほど同様500行分とします。先ほどのグラフでも分かる通り、歩行時のデータには振動がみられることからFFTを行い区間ごとの特徴量を算出します。

number_of_frames=500
instances = pd.DataFrame()
instance = 0
data.fillna(method='bfill')

for label in data.label.unique():
    start_position=0
    label_df = data[data['label']==label]

    while len(label_df) > start_position+number_of_frames:
        
        for metric in metrics:
            instance_df = label_df.iloc[start_position:start_position+number_of_frames].reset_index()
            instances.loc[instance, 'label'] = label
            instances.loc[instance, f'median_{metric}'] = instance_df[metric].median()
            instances.loc[instance, f'std_{metric}'] = instance_df[metric].std()
            fourier = np.fft.rfft(instance_df[metric])[1:]
            amplitude = max(np.abs(fourier))
            frequency = np.where(np.abs(fourier)==amplitude)[0][0]
            instances.loc[instance, f'amp_{metric}'] = amplitude
            instances.loc[instance, f'freq_{metric}'] = frequency
            instances.loc[instance, f'phase_{metric}'] = np.angle(fourier)[frequency]
        instance = instance + 1
        start_position = start_position + number_of_frames

行動の周波数に関する特徴量

各種の行動での特徴量を算出するため、まず振動の周波数について考えます。①立ち止まりおよび座り状態での静止、②歩行、③ジョギングで分けた際、③になるほど振動の周波数が大きいなることが考えられます。そこでそれぞれのデータの振動数の移動中央値の特徴量をヒストグラムで表示してみます。加速度センサは瞬間的な振動に対して高い値を検知する場合があるため、ここでは平均値ではなく中央値を使っています。

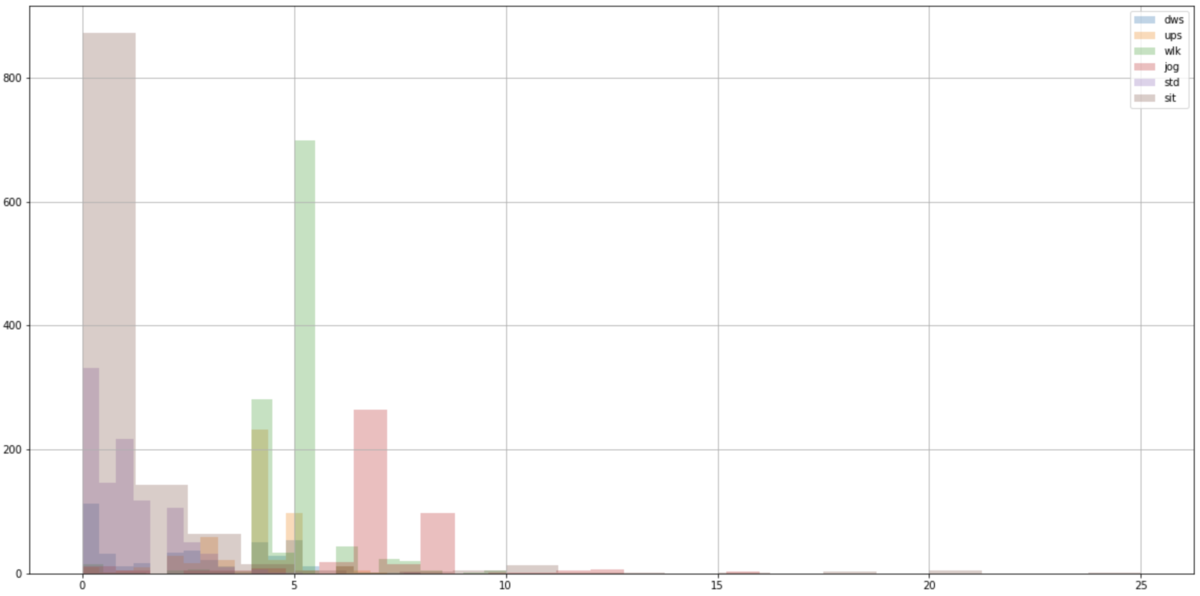
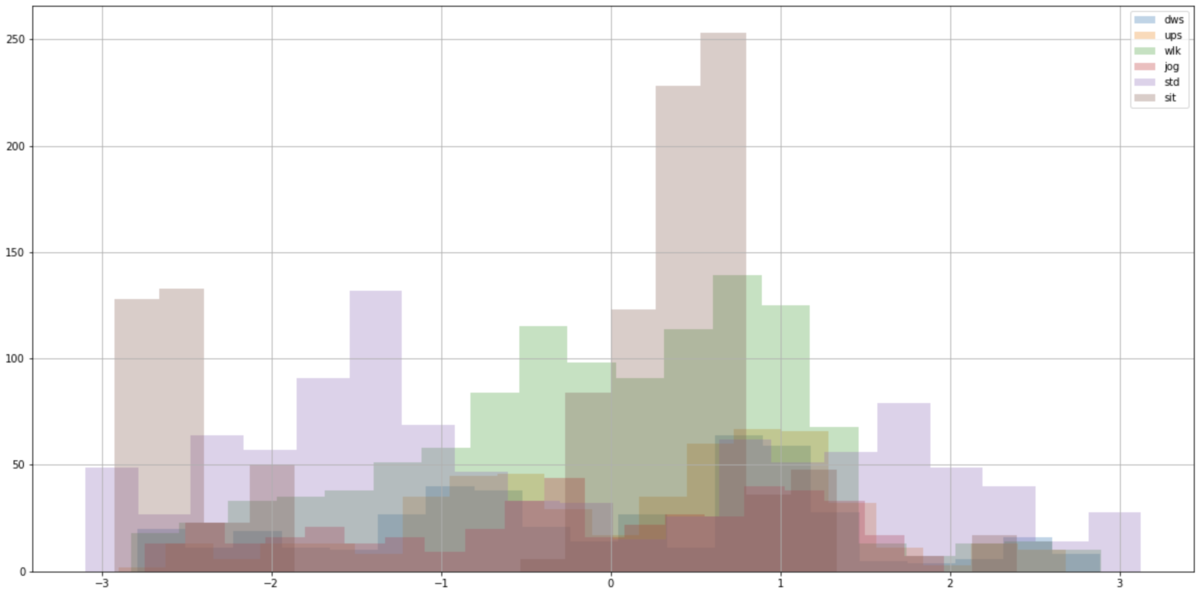
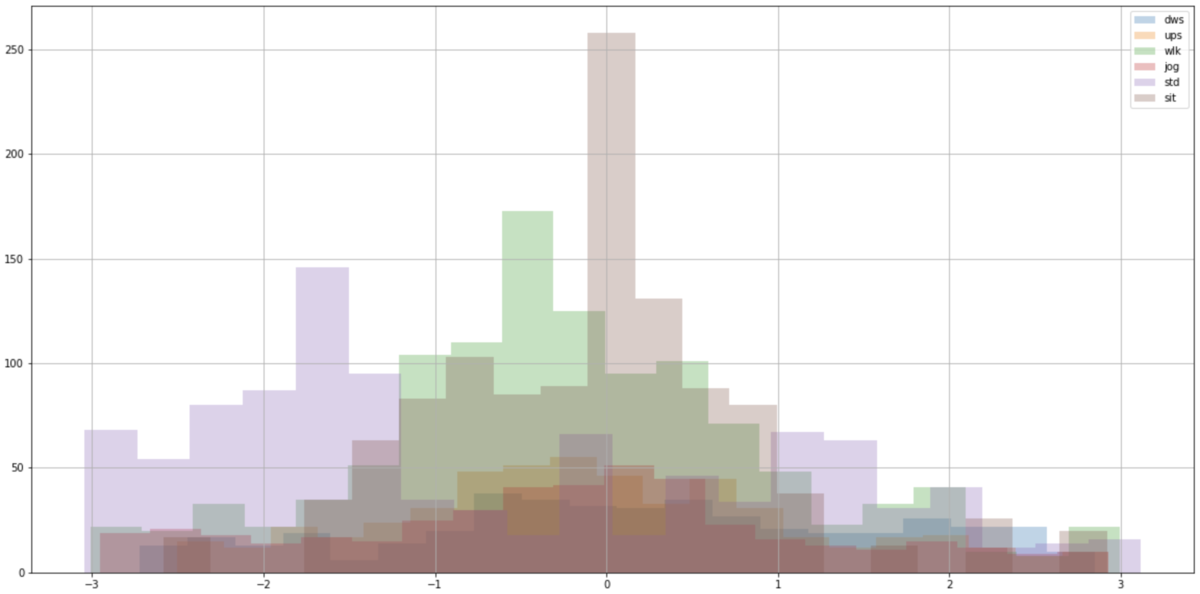
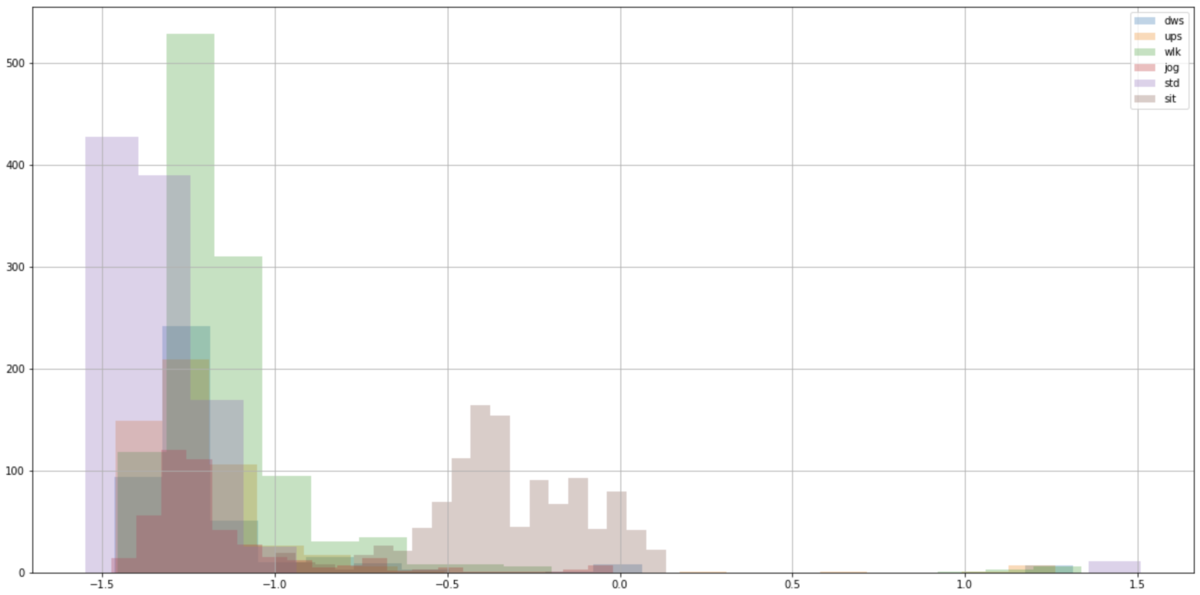
予想の通り、①立ち止まりおよび座り状態での静止（std, sit）、②歩行（wlk）、③ジョギング（jog）の順で振動の周波数が高いことがわかります。この特徴量によって立ち止まっているか歩行しているかの判別は付きそうです。それでは立ち止まり状態と座っている状態の判別はどのように行えるでしょうか。

姿勢角に関する特徴量

立ち止まり状態と座っている状態の判別にはセンサーの姿勢角が参考になるかもしれません。センサーの姿勢角（roll角、pitch角、yaw角）の特徴量をヒストグラムで表示したものが以下になります。roll、yawに関してはどの行動（歩行：wlk、座り:sit）においてもピークの位置が変わっているとは読み取れません。pitchに関してはこれが大きく異なります。理由として、このデータセットではポケットに縦向きにスマートフォンを入れて計測しているため、立っている状態と座っている状態でpitch角が90度ほど変化するからです。

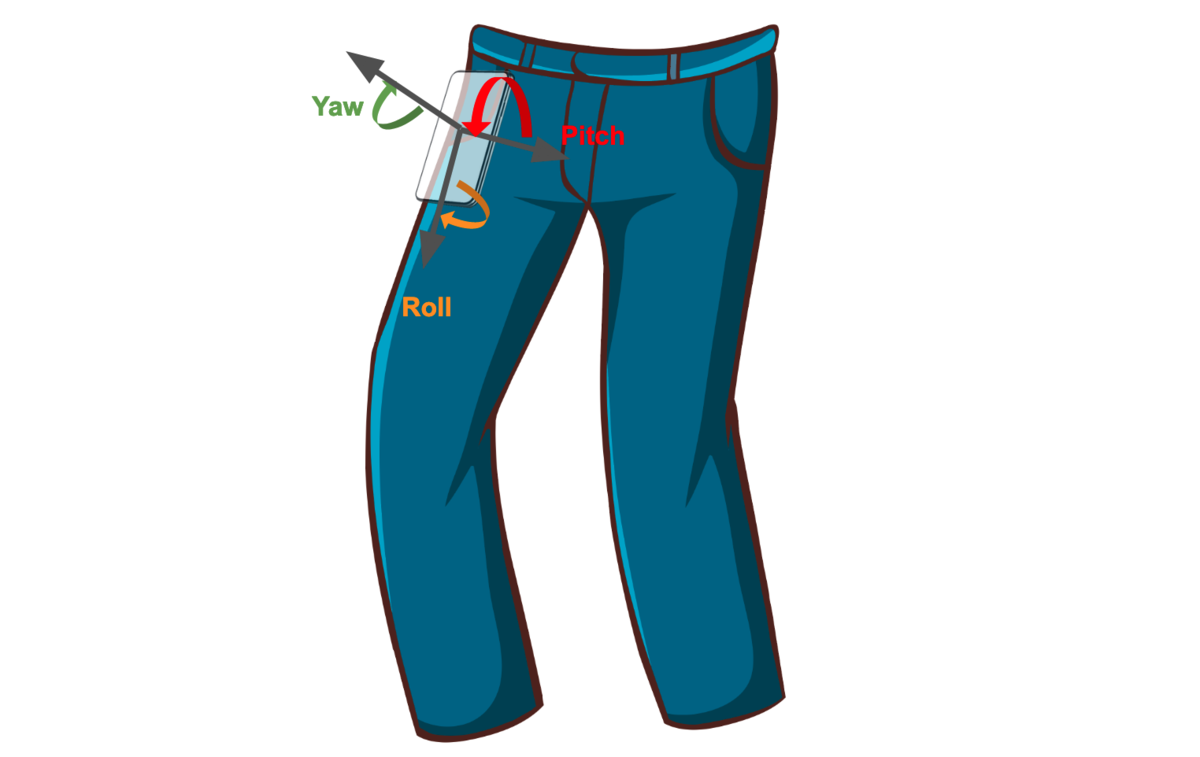
こうした特徴量の確認から、それぞれの行動内容の判別もできそうであることがわかりました。

学習

勾配ブースティングのモデルを使い、行動内容を判別していきます。はじめに決定木系のモデル特徴量の重要度を確認します。

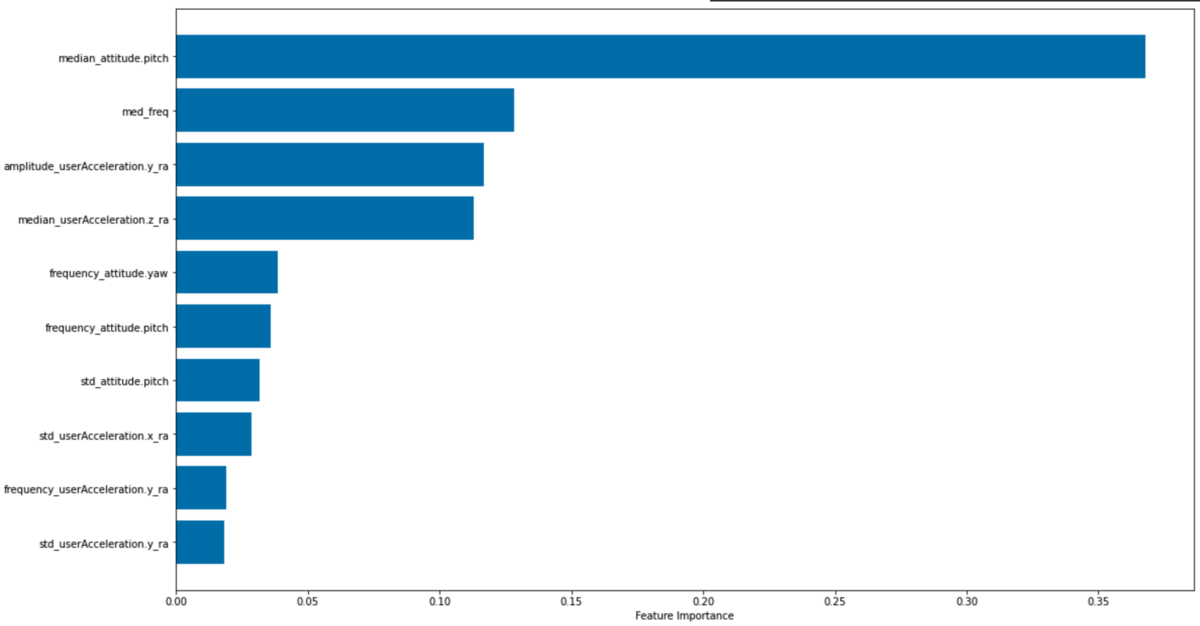
feature_importances = model.feature_importances_
idxSorted = np.argsort(feature_importances)[-10:]
barPos = np.arange(idxSorted.shape[0]) + .5
plt.barh(barPos, feature_importances[idxSorted], align='center')
plt.yticks(barPos, feature_names[idxSorted])
plt.xlabel('Feature Importance')
plt.subplots_adjust(left=0.2, right=0.9, top=0.9, bottom=0.1)
plt.show()

特徴量の重要度は以下のようになります。先ほど確認したpitch角情報がもっとも大きく寄与していることがわかります。次点でmed_freq（各センサの振動周波数）の重要度が高いことを確認できます。

次にデータをtrainとtestに分割した上で学習を行い判別精度の指標を算出します。マシューズ相関係数MCCを判別精度の指標として使用し、K-分割交差検証を行い平均精度を算出します。

y = instances.label
X = instances.drop('label', axis=1)
kf = KFold(n_splits=5, shuffle=True)
gbc_model = gbc()
MCC = []
for train_index, test_index in kf.split(X):
   X_train, X_test = X.loc[train_index], X.loc[test_index]
   y_train, y_test = y.loc[train_index], y.loc[test_index]
   gbc_model.fit(X_train, y_train)
   y_pred = gbc_model.predict(X_test)
   MCC.append(matthews_corrcoef(y_test, y_pred))
print(f"Mean MCC: {np.mean(MCC):.3f}")
print(f"Std of MCCs: {np.std(MCC):.4f}")
plot_confusion_matrix(gbc_model, X=X_test, y_true=y_test, labels=gbc_model.classes_, cmap='Blues')
plt.show()
plot_feature_importance(gbc_model, X_test.columns)

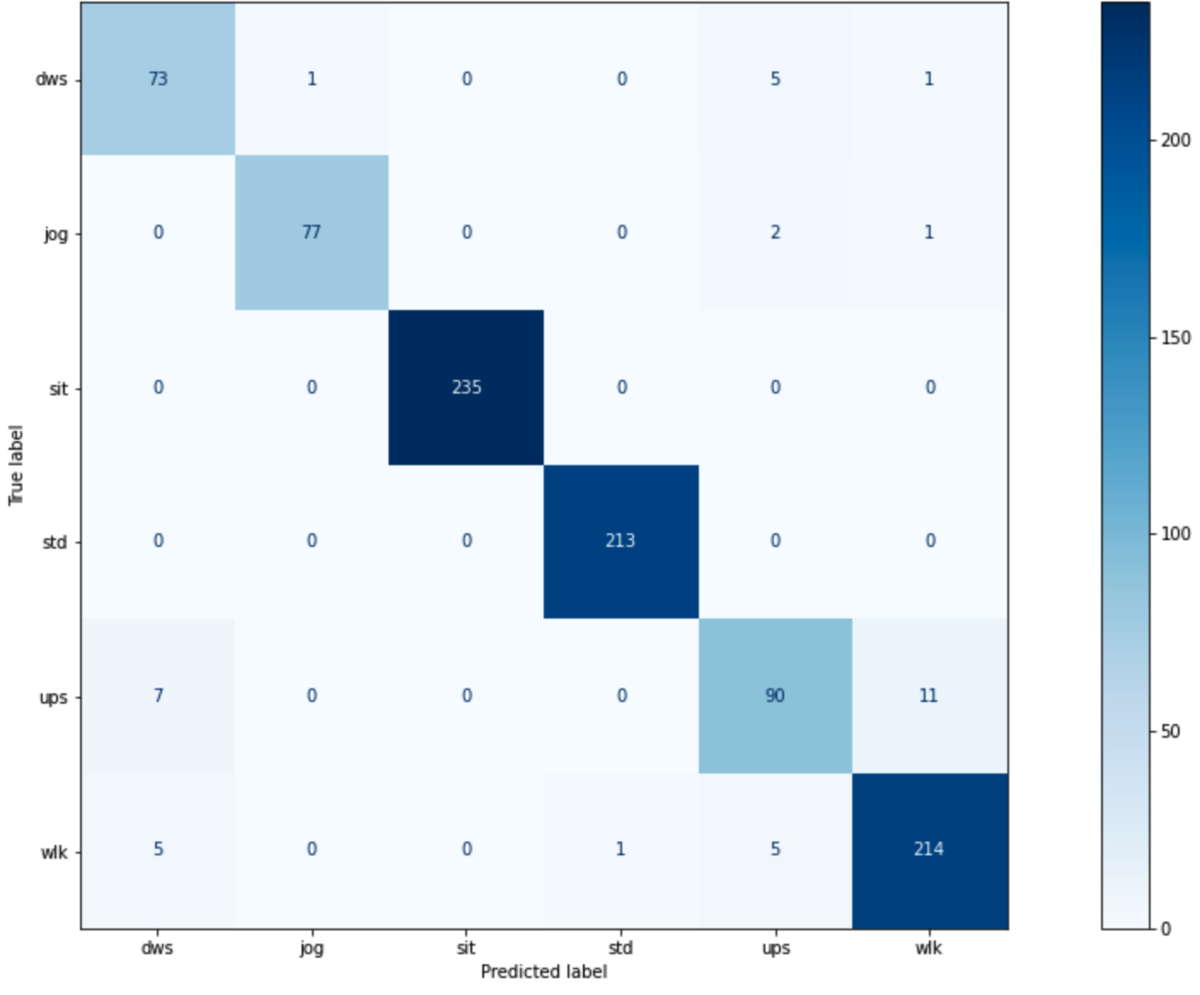
既存のデータセットに対してはMCCの平均は0.953という精度で判別が行えました。

分類

ここまで、iPhoneのセンサーを使用したデータセットで学習を進めてきました。同様の情報を収集できるように設定したM5Stackで、分類が行えるかどうかを確かめます。

下記の、実際に家の周りを歩いて計測したデータを用いて、作成したモデルを適用してみたところMCCの平均は0.920という精度で判別ができました。実際の現場での分類はまだですが近日中に実戦投入が行えればと考えています。

まとめ

加速度・角速度センサーを用いて、歩行や静止状態のどれに当てはまるかを分類しました。今回は簡易に計測と分類を行なってみましたが、実際に現場でどのようにセンサーをとりつけるか（ポケットの中にいれる、腰につける）なども重要だと考えられます。また計測前にキャリブレーションを行い、初期角度や加速度を補正することでセンサーの軸や特性に依存しない、機械学習で扱いやすいデータにできそうです。