はじめに

ABEJAアドベントカレンダー2023の11日目の記事です。この記事では不完全情報ゲームを解くための手法であるDeepNashについて紹介します。DeepNashはMastering the game of Stratego with model-free multiagent reinforcement learning(arXiv: Mastering the Game of Stratego with Model-Free Multiagent Reinforcement Learning)で提案されたモデルフリー強化学習をベースとした手法です。通常、強化学習を用いる場合エージェントが対戦相手に勝つことを目的として学習を行います。一方でDeepNashでは相手に勝つことを直接目指すのではなく、ナッシュ均衡を目指します。ナッシュ均衡を目指すことで相手がどんな手を打ったとしてもなるべく損をしない手を打てるようになる発想に基づいています。
この記事ではまず不完全情報ゲーム、ナッシュ均衡についての簡単な概要を説明した後、ナッシュ均衡を目指す方策更新手法であるRegularized Nash Dyamics(R-NaD)とそれを深層強化学習用に拡張したDeepNashについて解説します。
不完全情報ゲーム
ゲーム理論におけるゲームは、大きく完全情報ゲームと不完全情報ゲームの2つに分類されます。
完全情報ゲーム:すべてのプレイヤーがゲームの全情報を完全に知っているゲームです。具体的に言うと私的情報(手札などのそのプレイヤーしか見ることのできない情報)を持たず、同時手番でないゲームです。つまり、プレイヤーは自分の行動を決定する際に、他のプレイヤーが行動の選択に用いた情報を全て考慮に入れることができます。チェスや囲碁などが完全情報ゲームの例です。
不完全情報ゲーム:一部またはすべてのプレイヤーが意思決定に際してゲームの全情報を知ることができないゲームです。例えば、ポーカーやブリッジなどのカードゲームではプレイヤーは手札に基づいて行動を決定します。一方でそれぞれのプレイヤーは自分の手札ついての情報しか持っておらず、私的情報である他のプレイヤーの手札を知ることはできません。従って、例えば相手がレイズ(掛け金の上乗せ)をしてきた際にそれが実際に手札が強いためかこちらを降りさせるためのブラフなのかはわからないまま自分の行動を選択する必要があります。また、じゃんけんなどの同時手番ゲームにおいては相手の手を見る前に自分の手を決定しなければなりません。これらのゲームにおいては不完全な情報に基づいて行動を決定しなければならないことになります。このようなゲームを不完全情報ゲームと呼びます。
囚人のジレンマ
囚人のジレンマは、不完全情報ゲームの一例で、2人のプレイヤー(囚人)がお互いの選択を知らずに行動を選ぶゲームです。2人の囚人がそれぞれ独立に取り調べをうけており、それぞれの囚人は黙秘するか自白するかを選ぶことができるとします。自分と相手が黙秘/自白した場合に刑期は以下のようになるとします。
- 自分も相手も黙秘:自分も相手も懲役1年
- 自分は自白、相手は黙秘:相手だけ懲役10年
- 自分は黙秘、相手は自白:自分だけ懲役10年
- 自分も相手も自白:自分も相手も懲役6年
この状況では、2人の囚人がそれぞれ自分だけが有利になる選択(自白)をすると、結果的にはお互いが長期刑(懲役6年)になり、お互いが協力する選択(黙秘)をすればお互いが証拠不十分で短期刑(懲役1年)になります。また、一方だけが自白し、他方が黙秘した場合は黙秘した側は懲役10年、自白した側は減刑されて懲役0年となります。このことを表で表すと以下のようになります。表の数字のうち、1番目は自分の利得、2番目は相手の利得であるとします。

このゲームにおいて懲役を最小にするならどうするべきでしょうか? もちろん、相手も黙秘してくれるならば自身も黙秘することで懲役1年+懲役1年で合計懲役2年、これは自分と相手が受ける懲役の総和の中で最小となります。しかし、自身の懲役に着目するのであればこれは賢い選択ではありません。自分の黙秘に期待した相手は裏切って自白することで懲役を受けずに済まそうとするかもしれないからです(自分と相手は事前に黙秘するか自白するかを申し合わせることはできません)。そうなると自分としても自白して最悪の事態である懲役10年を避けた方が良さそうです。2人のプレイヤーが互いに最悪のケースを避けようとすると共に自白することとなります。
Matching Pennies
次にMatching Penniesについて説明します。Matching Penniesは二人用のシンプルなゲームで、それぞれのプレイヤー(プレイヤー1とプレイヤー2)が同時に表か裏を選択します。プレイヤー1の目的は互いの選択を一致させること、逆にプレイヤー2の目的は互いの選択を一致させないことです。
このゲームの利得表は以下のようになります:

このゲームは双方のプレイヤーの利得の和が常に0となるので零和ゲームです。例えば、両者がともに表を選んだ場合(プレイヤー1: 表, プレイヤー2: 表)、プレイヤー1は成功(+1の利得)し、プレイヤー2は失敗(-1の利得)となります。
このゲームも囚人のジレンマゲーム同様、各プレイヤーの最適の選択は相手の選択に依存します。例えば、プレイヤー1の最適手はプレイヤー2の選択が表の場合は表、裏の場合は裏となります。プレイヤー2の最適手はこの逆となります。このゲームはいずれのプレイヤーも自分の選択を逆にすることで勝敗が逆にできるという構造を持っています。そのため負ける側のプレイヤーにとっては常に選択を変えるインセンティブがあり、各プレイヤーが表か裏かの一方だけを必ず選ぶ形式のゲームとしてはこれは最善の戦略を持ちません。
設定を少し変えて各プレイヤーは確率
で表、
で裏を選ぶという設定とし、このゲームを多数回繰り返すこととします。このとき
となるので、プレイヤー1の期待利得は次のようになります。
また、零和ゲームであることからも成り立ちます。
例えばのケースを考えてみると
となります。このときプレイヤー2が利得を最大化する(=プレイヤー1の利得を最小化する)には
の値をなるべく小さくすればよいことになります。
とすれば
となるため、
となります。同様に考えていくと、
の場合プレイヤー2は
を適当に変えることによって
とできます。プレイヤー2についても同様に
のときも同様の議論ができるため、結局
が最善となります。
ナッシュ均衡
囚人のジレンマでは、両プレイヤーが自白する戦略がそれぞれのプレイヤーにとって最善となっていました。自身の選択を自白から黙秘に変えた場合、相手が自白のままである場合に利得が減ってしまうためです。また、matching penniesでは各プレイヤーがコインの表裏を確率でランダム選択する戦略が最善でした。確率を
から動かそうとすると相手の戦略次第では確率
のときより期待利得が減ってしまうためです。このように、他プレイヤーの戦略を固定した上で、自分の戦略を変更するインセンティブがないような戦略の組み合わせをナッシュ均衡と呼びます。
強化学習
DeepNashは強化学習をベースとした手法なので簡単に触れておきます。 強化学習はエージェントと環境という枠組みからなります。
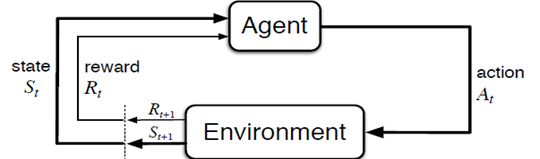
(図はReinforcement Learning: An Introductionから引用)
- エージェントは環境から状態
と報酬
を受け取る
- エージェントは状態に基づいて行動
を決める
- 環境は現在の状態と行動に応じて次の状態に遷移する
- エージェントは環境から状態
と報酬
を受け取る
エージェントと環境が上のようなサイクルを繰り返すとき、得られる報酬の総和が最大になるような方策を求める問題を解くことが強化学習の目的です。そのために強化学習においては報酬に基づいて状態の価値や行動の価値を推定することでより価値の高い行動(=より高い報酬の総和が期待できる行動)を取ることのできる方策を学習していきます。
もう少し詳しい説明は弊社ブログの以下の記事などが参考になると思います。
提案手法
完全情報ゲームである将棋や囲碁、チェスにおいては、強化学習と探索を組み合わせることで人間より強いエージェントを作ることにも成功しています。しかし、以下の理由から同様の手段は不完全情報ゲームにそのまま適用することは難しくなっています。
- 私的情報の存在により、情報状態空間が広い。例えば、ポーカーにおいては公開されている情報が同じであっても相手の手札が見えないために取りうる情報状態の総数は遥かに多くなります。そのため、各情報状態において最適方策を学習したり探索したりすることは計算量的に困難
- 相手の私的情報を推定する必要があるため、方策の評価が困難
- ゲームが大規模なので直接ナッシュ均衡を計算することは困難
この論文では、深層強化学習とゲーム理論を組み合わせてナッシュ均衡を目指して方策を学習することでこれらの問題を回避しています。以下ではまずR-NaDについて説明し、その後それを深層強化学習向けに拡張したDeepNashについて説明します。
Regularized Nash Dynamics (R-NaD)
まずR-NaDについて説明します。まず方策と正則化方策
を用意し、初期化しておきます。ここで、
はプレイヤーを表しており、
は他のプレイヤーを表しています。例えば、2人対戦ゲームでそれぞれのプレイヤーを
とすれば
のとき
です。正則化方策は実際のゲームプレイに用いる方策とは別に方策の更新の基準として用意した方策です。
以下の1から4を繰り返すことで学習を進めます。
- Generate Trajectory
- Reward Transformation
- Dynamics
- Update
Generate Trajectory
方策を用いて、
の系列を収集します。
はプレイヤー
の行動、
はプレイヤー
が得る報酬です。
Reward Transformation
報酬を次のように変形します。
第一項は元々の報酬で、第二項および第三項において方策および正則化方策
に依存する報酬を加えています。この報酬変換は次のDynamicsステップでナッシュ均衡への収束を保証する役割、これがエントロピー正則化として機能することで学習初期に方策が激しく変動することを防ぐ役割の2つの役割を兼ねています。
Dynamics
プレイヤーの行動
を取る確率
を以下の微分方程式に従って更新します。
]
ここで]で、相手の方策
が固定されている時の行動
の価値を表しています。大括弧の中は
が行動価値の期待値
をどれだけ上回っているかを示しています。全体の正負は大括弧の中の正負に一致するので、期待値より高い価値を持つ行動を取りやすく、そうでない行動を取りにくくなるように方策が更新されます。この微分方程式は不動点
を持ち、更新を繰り返すことで不動点に向かって収束します。
Update
Dynamicsにおいての更新を十分な回数繰り返すと不動点
に近づきます。その状態の
を次の正則化方策
とします。
は
が大きくなるにつれてナッシュ均衡に近づきます。
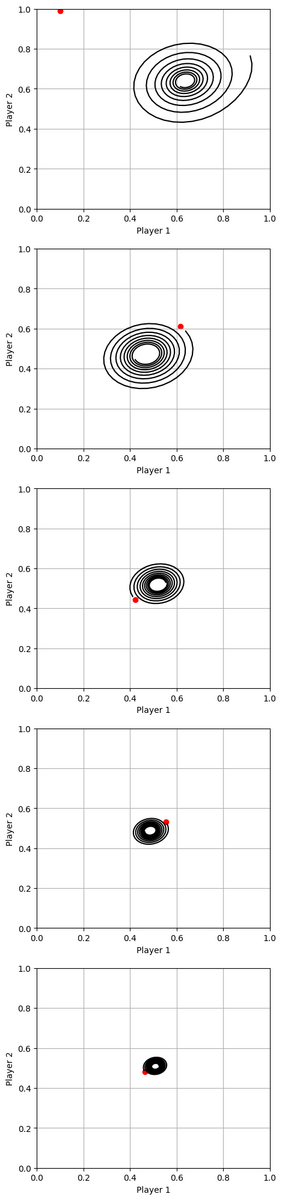
R-NaDをMatching Penniesに適用してみましょう。ただし、今回は表裏を1回選択するだけのゲームであり、報酬および価値の期待値は解析的にわかるのでトラジェクトリの収集部分は省いています。コードは以下の通りです。
# Player 1とPlayer 2がHeadを選ぶ確率をそれぞれp1, p2とする p1 = 0.9 p2 = 0.8 # 正規化用のPolicy。0 < p < 1なら任意の値でいい。 p1_reg = 0.1 p2_reg = 0.99 # 学習率 lr = 0.05 # 正規化項の係数 eta = 0.2 fig, axs = plt.subplots(5, 1, figsize=(5, 25)) for i in range(5): p_list = [] reg_p_list = [[p1_reg, p2_reg]] for _ in range(300): # Reward Transformations r_1_00 = 1 - eta * np.log(p1/p1_reg) + eta * np.log(p2/p2_reg) r_1_01 = -1 - eta * np.log(p1/p1_reg) + eta * np.log((1-p2)/(1-p2_reg)) r_1_10 = -1 - eta * np.log((1-p1)/(1-p1_reg)) + eta * np.log(p2/p2_reg) r_1_11 = 1 - eta * np.log((1-p1)/(1-p1_reg)) + eta * np.log((1-p2)/(1-p2_reg)) r_2_00 = -1 + eta * np.log(p1/p1_reg) - eta * np.log(p2/p2_reg) r_2_01 = 1 + eta * np.log(p1/p1_reg) - eta * np.log((1-p2)/(1-p2_reg)) r_2_10 = 1 + eta * np.log((1-p1)/(1-p1_reg)) - eta * np.log(p2/p2_reg) r_2_11 = -1 + eta * np.log((1-p1)/(1-p1_reg)) - eta * np.log((1-p2)/(1-p2_reg)) # Estimate Q-value q_1_0 = p2 * r_1_00 + (1 - p2) * r_1_01 q_1_1 = p2 * r_1_10 + (1 - p2) * r_1_11 q_2_0 = p1 * r_2_00 + (1 - p1) * r_2_01 q_2_1 = p1 * r_2_10 + (1 - p1) * r_2_11 # Estimate Advantage a_1_0 = q_1_0 - (p1 * q_1_0 + (1 - p1) * q_1_1) a_1_1 = q_1_1 - (p1 * q_1_0 + (1 - p1) * q_1_1) a_2_0 = q_2_0 - (p2 * q_2_0 + (1 - p2) * q_2_1) a_2_1 = q_2_1 - (p2 * q_2_0 + (1 - p2) * q_2_1) # Dynamics p1 = p1 + lr * (a_1_0 - a_1_1) p2 = p2 + lr * (a_2_0 - a_2_1) p_list.append([p1, p2]) axs[i].plot(np.array(p_list)[:, 0], np.array(p_list)[:, 1], c='black') axs[i].scatter(np.array(reg_p_list)[:, 0], np.array(reg_p_list)[:, 1], c='r') axs[i].set_xlim(0, 1) axs[i].set_ylim(0, 1) axs[i].grid(True) axs[i].set_xlabel('Player 1') axs[i].set_ylabel('Player 2') # Update Regularization Policy p1_reg = p1 p2_reg = p2 reg_p_list.append([p1_reg, p2_reg]) plt.show()
上記のコードを実行すると結果は以下のようになります。黒の実線はの軌跡を表しており、赤点は開始時点での
を表しています。
が徐々に
に近づく様子がわかります。
DeepNash
DeepNashはR-NaDに自己対戦と深層強化学習と組み合わせたものです。R-NaDは状態を表形式で扱う前提の手法であるため、そのままでは状態空間が広いゲームに適用することができません。深層強化学習と組み合わせ、方策関数をニューラルネットで近似することで大規模なゲームにも適用できるようになります。この節ではDeepNashのアルゴリズムについて説明を行うものとし、式などは基本的に論文中の記述に合わせていますが、実装上のテクニカルな部分については省いてあります。
深層強化学習の手法を用いるために、次のようなニューラルネットワークを作ります。Pyramid ModuleはObservationから特徴を抽出し、その特徴を用いてPolicy Headは方策を、Value Headは状態の評価値を出力します。
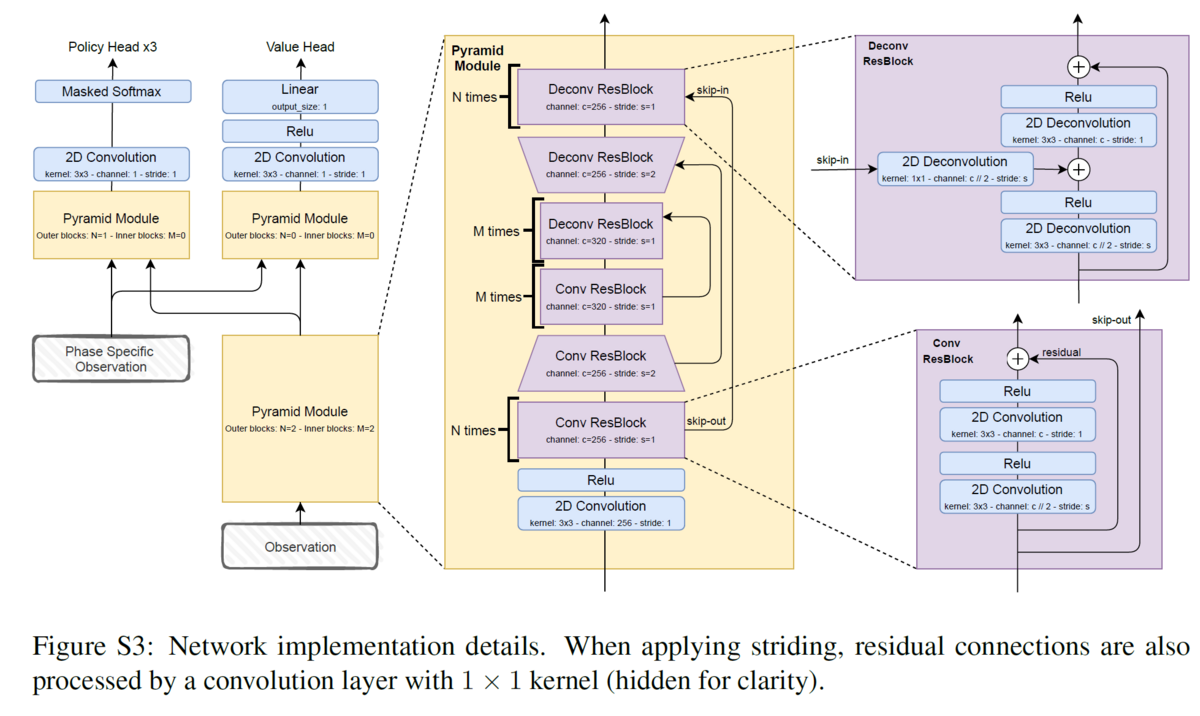
まず方策と正則化方策
を用意し、初期化しておきます。以下の1から5を繰り返すことで学習を進めます。
- Generate Trajectory
- Reward Transformation
- Value Estimation
- Dynamics
- Update
Generate Trajectory
方策を用いて自己対局によりトラジェクトリを収集します。
Reward Transformation
得られたトラジェクトリの各を以下のように補正します。R-NaDの時と同様です。
はゲームの履歴のこととして論文中で扱われていますが、ここでは状態として解釈して問題ないです。
は履歴の中でエージェントが観測可能な情報を意味します。
Value Estimation
Reward Transformationで変換した報酬を用いて状態価値と行動価値
を推定します。エピソード終了時の時刻を
、その状態の推定状態価値を
で初期化します。
で初期化しておきます。また、v-trace用のパラメータである
を
で初期化します(v-traceについてはこの記事内では説明しませんが、トラジェクトリを収集する時に用いた方策と学習中の方策が異なることから生じる差を補正する方法の一種です)。その後、
から始めて
まで以下のように処理していきます。
ターンに行動しているプレイヤーが
でないとき
ターンに行動しているプレイヤーが
のとき
まずv-trace用のパラメータを更新します。
その後、価値の推定を行います。
ここで
です。
Dynamics
状態評価のネットワーク(Value Head)と方策のネットワーク(Policy Head)をそれぞれ以下の損失関数で学習します。
ただし、とし、
はターン
に行動しているプレイヤーを指すものとします。
大雑把に、は状態評価のネットワークの出力がValue Estimationの節で得られた推定価値
に近くなるような学習、
は方策のネットワークが平均より高い
を持つ
を取りやすく、そうでない
を取りにくくなるように学習を促します。これらの工夫を入れて自己対戦を繰り返すことでナッシュ均衡戦略を目指した強化学習を行っています。
Update
R-NaDと同様です。
StrateGoへの適用
著者はこの手法をStrateGoという軍人将棋に似たゲームに適用しています。StrateGoにおけるDeepNashの有効性について説明するために、まずStrateGoのルール概要を説明します。
ゲームは2つのフェーズに分かれています。
フェーズ1:コマの設置 各プレイヤーは相手にわからないように自陣側の4列に計40枚の駒を配置します。

40枚の内訳は以下の表の通りです。StrateGoには12種類の駒があり、それぞれ強さや移動範囲が異なります。ScoutやMinerなどの低位の駒は枚数が多く、MarshalやGeneralなどの高位の駒は枚数が少なくなっています。

フェーズ2:ゲームプレイ 各プレイヤーは交互に駒を動かしていきます。移動範囲も駒の種類ごとに異なっており、基本的には1マスの移動が可能ですがB(Bomb)やF(Flag)は移動できません。また、盤上の水色の領域には進入できません。移動先に相手の駒がある場合、数字が大きい側の駒が勝ちます。ただし、2のSpyと10のMarshalが接触した場合はSpyの側が勝ちます。また、Bに接触した駒は負けてしまいます(ただし、接触したのがMinerの場合は爆弾を解除できるのでMinerが勝ちます)。ゲームの勝利条件は相手のFの駒に接触することです。
戦績
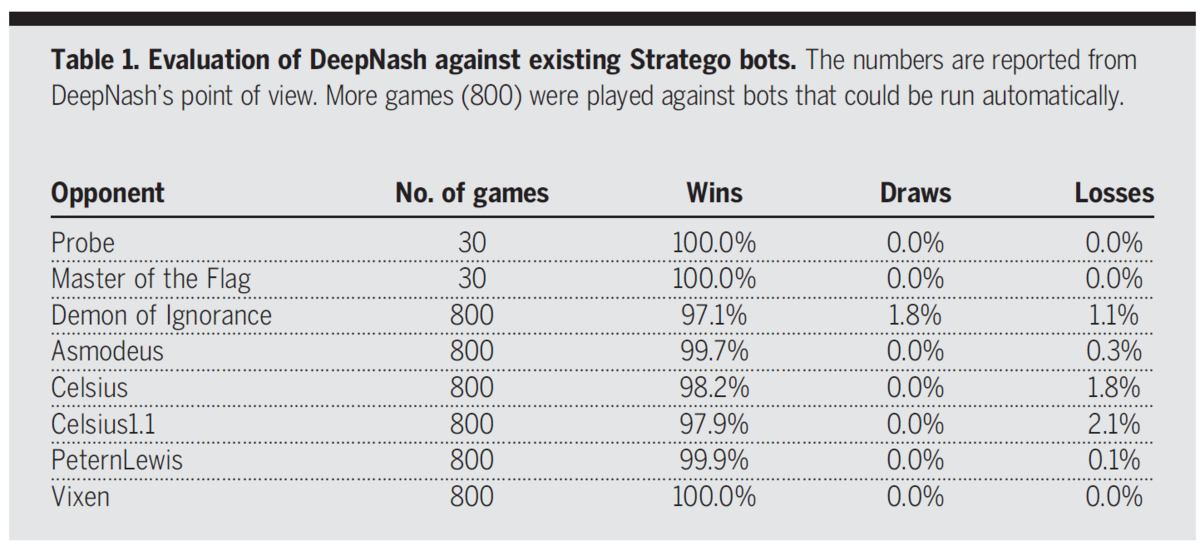 既存のStrateGoのAIに対して少なくとも97%の勝率となっており圧倒的です。また、トップレベルの人間プレイヤーに対しても50戦の対戦を行って42戦の勝利(勝率84%)となっていました。
既存のStrateGoのAIに対して少なくとも97%の勝率となっており圧倒的です。また、トップレベルの人間プレイヤーに対しても50戦の対戦を行って42戦の勝利(勝率84%)となっていました。
DeepNashの特徴
駒と情報のトレードオフの考慮
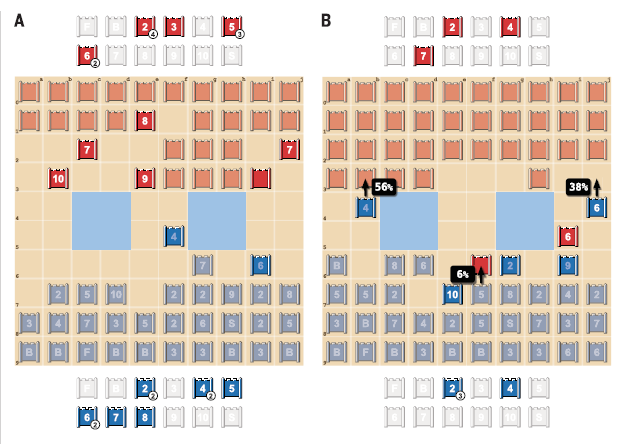
不完全情報ゲームにおいては、盤面そのものでは不利であっても情報の面で優位ということがありえます。上図Aにおいて、青は7や8といった強い駒を失っていますが、その代わりに相手の10、9、8、7×2の位置を明らかにしています。逆に、青の高ランクの駒の位置はほとんど相手にばれていません。DeepNashの価値関数は、駒数の不利にもかかわらずこの盤面を青側有利と判断しており、実際にこの試合は青が勝利したようです。 また上図Bにおいて、青は9で赤の6を取ることが可能であるにもかかわらず実際にはDeepNashはほとんどその手を打たないようです。つまり、駒を1つ取ることよりも9の正体を隠す方が有利であると判断していることになります。 これらの結果から、DeepNashは盤面や駒の数だけでなく情報面の優位性を考慮した決定を下せることがわかります。
DeepNashはブラフを張ることができる
論文中ではDeepNashは相手が知らない情報を利用して盤面の優位に繋げる、つまりブラフを張ることができることを示しています。
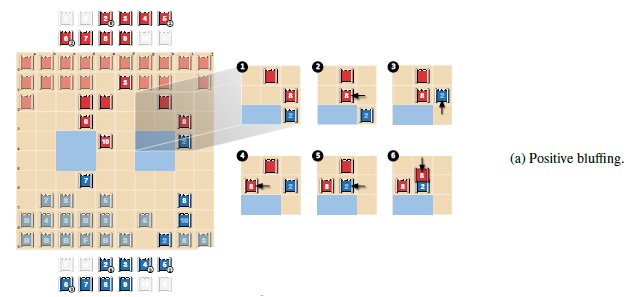
(A)においては、まず赤の8が青の2(赤視点ではまだランクは不明)から逃げ、それを青の2が追いかけています。つまり、実際に当たれば青の2は赤の8に負ける駒であるにもかかわらず、8より強い駒であるかのように振る舞うブラフを行っています。
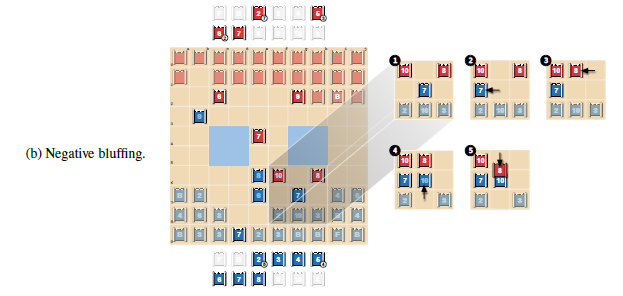
(B)においては、赤の8の前に青の10を進めています。これは赤の視点ではスパイを10に近づけているように見えるため、8でそれを倒そうとして逆に青の10に返り討ちにあう様子を示しています。このように、DeepNashは駒を強く見せかけるブラフだけでなく弱く見せかけるブラフも行うことができるようです。
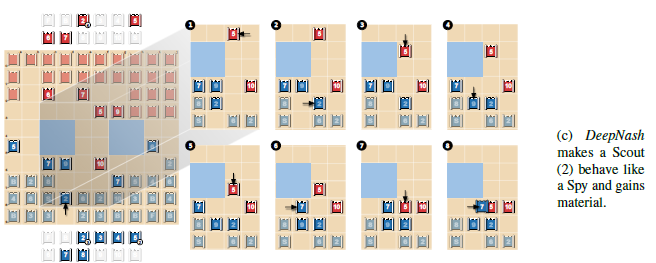
(C)ではより複雑なブラフを行っています。まず青の2を赤の10に近づけることでこれをスパイに見せかけています。赤はスパイかもしれない青の2を倒すために赤の5を進め、結果的に青は7を使って5を取ることに成功しています。
おわりに
強化学習とゲーム理論を組み合わせることで不完全情報ゲームを攻略するDeepNashについて紹介しました。手堅いだけではなく、相手と自分が知っている情報の差を利用してブラフを張ることもできるという点で非常に面白い手法です。また、ゲームの種類に依存しないので、適用範囲も広いと思われます。今後これを実装して実験をしてみたいと思っています。
