ABEJA Tech Blog

中の人の興味のある情報を発信していきます

トップ > 宇宙 > Starlinkに会いに行こう：Go言語で人工衛星の位置計算にチャレンジ

Starlinkに会いに行こう：Go言語で人工衛星の位置計算にチャレンジ

宇宙

はじめに

ABEJA大田黒です。少し真面目な話題の記事が続いたので、閑話ネタになります。昔、このような記事を執筆しました。
tech-blog.abeja.asia


最近、普及が加速しているStarlink。ついに、スマートフォン単体で低軌道のStarlink衛星と直接通信できるサービスも登場し、宇宙を利用した通信ネットワークがぐっと身近になったと感じる今日この頃です。さて、ふと疑問に思いました。今、地球の周りにはどれくらいの数のStarlink衛星が存在しているのでしょうか？また、それらの衛星はどのように死角をカバーしながら地球全体を覆っているのでしょうか？エンジニアとしては、気になって夜も眠れません。

そこで今回のゴールは、数値計算を通じて、以下を明らかにすることです。

  • 今、人工衛星はどこの国の上空にいるのか？
  • インサイト（観測）時、どの方角から現れるのか？
  • どんな速度ベクトルで運動しているのか？

ケプラーの法則とGoを使って、衛星のリアルタイムな動きを追いかけていきます！

必要知識

今回計算例を示すに当たり、色々と専門用語が出てきます。

TLE (Two Line Element)

TLE（Two-Line Element set）は、人工衛星の軌道を表現するためのフォーマットで、NORAD(北アメリカ航空宇宙防衛司令部)などが提供しています。2行のテキストで構成され、衛星の軌道傾斜角、離心率、平均運動、近地点引数、元期などが含まれています。これらの要素を用いることで、指定時刻における衛星の位置や速度を計算できます。軌道予測や地上局追跡に不可欠なデータです。


出典： G-Portal JAXA

ケプラーの方程式 (第二法則：面積速度一定)

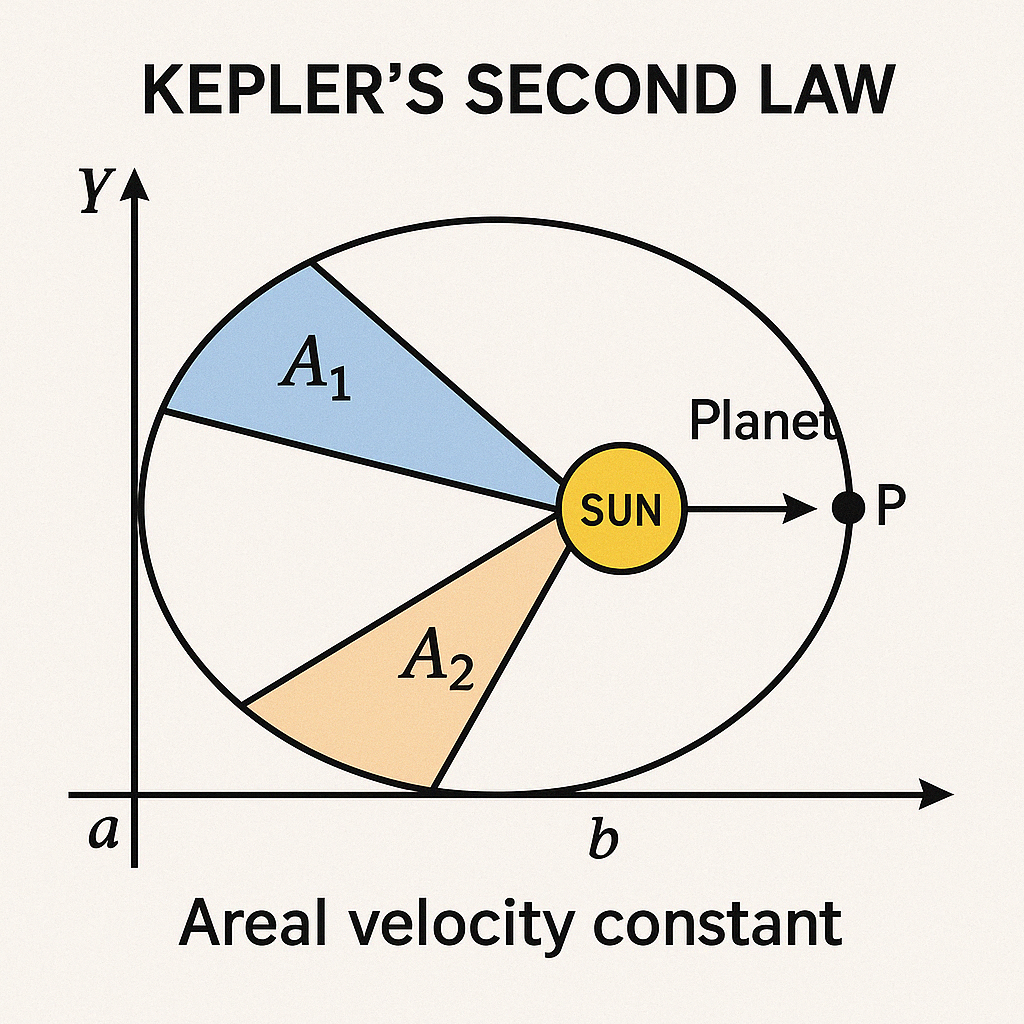
この法則は「惑星は太陽と自分を結ぶ直線が、等時間に等しい面積を掃くように動く」と定義されます。これにより、衛星は常に一定の速度で移動しているわけではなく、太陽（または重力源）に近い時は速く、遠い時は遅く移動します。工学的には、角運動量保存の結果と捉えることができます。中心力（重力）によって衛星は常に中心方向に引かれているため、外力によるトルクが発生せず、軌道面上の角運動量が一定になります。その結果、単位時間あたりに掃かれる面積（面積速度）が一定になります。

使い所：軌道計算では、ケプラー方程式 を数値的に解き、衛星の位置を特定します。その根底にはこの第二法則が流れています。軌道上の速度変化と位置を結びつける強力な法則です。

ケプラーの方程式 (第三法則：公転周期の2乗 ∝ 軌道長半径の3乗)


ケプラーの第三法則は、「惑星の公転周期の2乗は、その軌道長半径の3乗に比例する」という法則です。これは、衛星や惑星がどれだけの時間で公転するかを、軌道の大きさ（長半径）から予測できる強力な関係式を与えてくれます。この法則は太陽系の惑星だけでなく、人工衛星や他の天体にも適用可能で、特に中心天体（太陽や地球）の質量が分かっている場合には、比例定数を含めたより正確な計算式が使われます。
この関係式から、軌道を高くすればするほど衛星の公転速度は遅くなることがわかります。例えば、GPS衛星や静止衛星が高高度にあるのは、この法則によって得られる公転周期の調整が理由です。軌道設計やミッション計画において極めて基本かつ重要な物理法則の一つです。

本初子午線　（Prime Meridian）

本初子午線は、経度0度と定義される基準の子午線で、現在はイギリス・グリニッジ天文台を通る子午線が国際的に採用されています。地球固定座標系（ECEF）では、この本初子午線がX軸方向の基準になります。人工衛星の位置を緯度・経度で表す際にも、この本初子午線との角度差が「経度」として使われます。

春分点　（Vernal Equinox Point）

春分点は、天球上で太陽が春分の日に天の赤道と黄道を交わる点を指し、天文座標系（ECI）におけるX軸の基準となります。地球が自転してもこの方向は変化しないため、慣性系の基準として用いられます。衛星軌道の昇交点赤経なども、この春分点を基準に角度を測定します。

グリニッジ恒星時　（Greenwich Sidereal Time: GST)

地球は自転していますが、私たちが普段使っている「太陽時」は太陽の見かけの動きに基づいています。一方、「恒星時」は遠くの恒星（天球上の固定された星）を基準にした時間です。宇宙に浮かぶ物体（人工衛星など）の軌道は、地球の自転と宇宙座標系の関係を知る必要があります。これを計算するために、「地球が宇宙に対して今どっちを向いているか」を表す時間が必要です。それがグリニッジ恒星時になります。

計算の流れ（全体像）

ゴール達成に必要な計算ステップは下記になります。後ほど詳しく説明します。

  1. TLEを解析
  2. 元期からの経過時間を計算
  3. 軌道長半径を計算
  4. 平均近点角を更新
  5. ケプラー方程式を解き、離心近点角を得る
  6. 軌道面上の(u,v)座標を得る
  7. 摂動補正を適用
  8. 軌道面座標からECI座標系に変換
  9. 地球自転を考慮してECEF座標系へ変換
  10. 緯度・経度・高度を求める


人工衛星の位置を求めるには、まずTLE（Two Line Element）データを解析し、衛星の軌道情報を取得する必要があります。TLEには衛星の軌道傾斜角や離心率、平均近点角などが含まれ、これらをもとに計算を進めます。次に、TLEが示す元期（観測基準時）から現在までの経過時間を計算し、その間に軌道要素がどの程度変化したかを推定します。これに基づき、ケプラーの第三法則を利用して軌道長半径を計算します。軌道長半径は、衛星の平均的な地球からの距離を示します。さらに、時間経過を反映して平均近点角を更新します。平均近点角は衛星が軌道上のどの位置にいるかを示しますが、直接位置は求まらないため、ケプラー方程式をニュートン・ラフソン法で解き、離心近点角を算出します。離心近点角が求まると、衛星の軌道面上での(u,v)座標を得ることができます。続いて、地球の扁平さに起因する摂動（J2効果）を考慮し、昇交点赤経や近地点引数を微修正します。これらを反映し、軌道面座標を地球中心慣性座標系（ECI系）へ変換します。さらに地球自転を考慮して、地球固定座標系（ECEF系）へと座標を回転させます。最後に、ECEF座標から緯度・経度・高度を算出することで、地球上の衛星の現在位置を特定することができます。


各部の計算の流れ

TLEを解析

衛星の位置を推定するためには、まずTLE（Two Line Element）データを読み取る必要があります。TLEには、軌道傾斜角、離心率、平均近点角、平均運動など、軌道を特徴づけるパラメータが含まれています。これらを正確に抽出し数値化することで、後続の軌道計算が可能になります。TLEは固定フォーマットで提供されるため、文字列を決められた桁で区切って読み取る処理が必要です。ここでのパースミスは、以降の計算に大きな誤差を生むため、丁寧な取り扱いが求められます。

// TLEから抽出した軌道要素を格納する構造体
type TleOrbitalElement struct {
	meanAnomaly        float64 // 平均近点角 [Degree]
	meanMotion         float64 // 平均運動 [Rev/Day]
	MeanMotionDot      float64 // 平均運動変化係数 [Rev/Day²]
	eccentricity       float64 // 離心率 [-]
	etYear             int     // 元期 [Year]
	etDay              float64 // 元期 [Day]
	orbitalInclination float64 // 軌道傾斜角 [Degree]
	raan               float64 // 昇交点赤経 [Degree]
	argumentOfPerigee  float64 // 近地点引数 [Degree]
}

// TLE文字列から軌道要素を抽出する関数
func parseTle() *TleOrbitalElement {
	// TLEサンプルデータ（STARLINK-1008）
	str1 := "1 44714U 19074B   25117.42924319 -.00001157  00000+0 -58773-4 0  9990"
	str2 := "2 44714  53.0517 166.3609 0001116  99.1558 260.9557 15.06400606301084"

	// 各行をスペースで区切る
	a := strings.Split(str1, " ")
	b := strings.Split(str2, " ")

	// 元期データのパース
	etYear, _ := strconv.Atoi(fmt.Sprintf("20%s", a[5][0:2]))
	etDay, _ := strconv.ParseFloat(a[5][2:], 64)
	firstTimeDerivativeOfTheMeanMotion, _ := strconv.ParseFloat(fmt.Sprintf("0%s", a[7]), 64)

	// 軌道要素のパース（TLE 2行目は固定幅）
	orbitalInclination, _ := strconv.ParseFloat(strings.TrimSpace(str2[8:16]), 64)
	rightAscensionOfAscendingNode, _ := strconv.ParseFloat(strings.TrimSpace(str2[17:25]), 64)
	eccentricity, _ := strconv.ParseFloat("0."+strings.TrimSpace(str2[26:33]), 64)
	argumentOfPerigee, _ := strconv.ParseFloat(strings.TrimSpace(str2[34:42]), 64)
	meanAnomaly, _ := strconv.ParseFloat(strings.TrimSpace(str2[43:51]), 64)
	meanMotion, _ := strconv.ParseFloat(strings.TrimSpace(str2[52:63]), 64)

	// 構造体に格納して返す
	return &TleOrbitalElement{
		meanAnomaly:        meanAnomaly,
		meanMotion:         meanMotion,
		MeanMotionDot:      firstTimeDerivativeOfTheMeanMotion,
		eccentricity:       eccentricity,
		etYear:             etYear,
		etDay:              etDay,
		orbitalInclination: orbitalInclination,
		raan:               rightAscensionOfAscendingNode,
		argumentOfPerigee:  argumentOfPerigee,
	}
}

元期からの経過時間を計算

TLEが示す情報は「ある時点」の衛星の状態を表しています。そのため、観測したい時間における位置を求めるには、TLEの元期（Epoch）から現在時刻までの経過時間を日単位で計算する必要があります。経過時間は、平均近点角の更新や軌道要素の微調整に直接影響する重要な値です。UTC時間を基準に、元期との差分を正確に求める必要があります。

func calculateTimeDifference(targetTime time.Time, epocTimeYear int, epocTimeDay float64) float64 {
	tmp := time.Date(targetTime.Year(), time.January, 1, 0, 0, 0, 0, time.UTC)
	t_diff1 := float64(targetTime.Unix()-tmp.Unix())/86400.0 + 1.0

	tmp = time.Date(epocTimeYear, time.January, 1, 0, 0, 0, 0, time.UTC)
	tmp = tmp.Add(time.Duration(float64(time.Second) * 86400.0 * epocTimeDay))
	tmp2 := time.Date(epocTimeYear, time.January, 1, 0, 0, 0, 0, time.UTC)
	t_diff2 := float64(tmp.Unix()-tmp2.Unix()) / 86400.0

	t_diff := t_diff1 - t_diff2
	if t_diff < 0.0 {
		panic("TargetTime < ET")
	}
	return t_diff
}

軌道長半径を計算

軌道長半径（a）は、衛星の平均的な地球からの距離を示し、衛星の運動エネルギーとバランスしています。TLEから得られる「平均運動」（1日に何周するか）をもとに、ケプラーの第三法則を用いて軌道長半径を算出します。ここでは地球の重力定数を考慮した計算式を使い、衛星が回る楕円軌道のサイズを正確に求めます。

func calculateOrbitalSemiAxes(meanMotion float64) (float64, float64) {
	a := math.Cbrt((2.975537 * math.Pow(10, 15)) / (4 * math.Pi * math.Pi * meanMotion * meanMotion))
	b := math.Sqrt(a*a - a*a*0.0001679*0.0001679)
	return a, b
}

平均近点角を更新

元期から時間が経過すると、衛星は軌道上を進んでいます。現在時点での衛星の平均近点角を求めるため、元期の平均近点角に経過時間×平均運動を加算し、必要に応じて平均運動の変化率も考慮します。この更新により、衛星が軌道上のどの位置にいるかを大まかに把握できるようになります。ここでは単純な加算と二次項補正を含む計算が必要です。

func calculateMeanAnomaly(m0, m1, m2, t_diff float64) float64 {
	m := (m0 / 360.0) + m1*t_diff + 0.5*m2*t_diff*t_diff
	fracM := m - float64(int64(m))
	fracM_Radian := fracM * (2 * math.Pi)
	return fracM_Radian
}

ケプラー方程式を解き、離心近点角を得る

平均近点角は「平均的な進み具合」を示す指標にすぎず、実際の軌道上の位置はさらに離心近点角を求める必要があります。離心近点角は、ケプラー方程式 M=E−e・sinE を解くことで得られます。ただしこの方程式は代数的に解けないため、ニュートン・ラフソン法を用いて数値的に収束計算を行います。このプロセスによって、衛星の位置を高精度に推定するための鍵となる角度を得ることができます。

func KeplerEquation(e, M float64) func(Ebefore float64) float64 {
	return func(Ebefore float64) float64 {
		FE := Ebefore - e*math.Sin(Ebefore) - M
		Eafter := Ebefore - FE/(1-e*math.Cos(Ebefore))
		return Eafter
	}
}

func NewtonRaphson(e, before, a float64) (float64, float64) {
	equation := KeplerEquation(e, before)
	var after float64
	err := 100.0
	for i := 0; i < 10; i++ {
		after = equation(before)
		err = math.Abs(after - before)
		before = after
	}
	return after, err
}

軌道面上の(u,v)座標を得る

離心近点角が得られると、衛星の軌道平面上での位置(u, v)を計算できます。これは、楕円軌道上における直交座標であり、次式に基づいて算出されます：

ここで得られる座標は、あくまで衛星の軌道面内での位置を示すもので、地球に対する三次元的位置を得るためにはさらに座標変換が必要です。

func calculatePositionInOrbitalPlane(a, ecc, eccentricAnomaly float64) (float64, float64) {
	u := a*math.Cos(eccentricAnomaly) - a*ecc
	v := a * math.Sqrt(1-ecc*ecc) * math.Sin(eccentricAnomaly)
	return u, v
}

摂動補正を適用

地球は完全な球体ではなく赤道方向に膨らんだ楕円形をしているため、衛星の軌道要素（特に昇交点赤経や近地点引数）は時間とともにわずかに変化します。この摂動（主にJ2項による地球の非球対称重力場効果）を簡易モデルで補正します。摂動を無視すると、衛星の位置計算に少しずつ誤差が蓄積してしまうため、長期間精度を保つには必須のステップです。J2って聞くとサッカーを思い出しますね。

func calculatePerturbationCorrection(angleOmegaA0, angleOmegaB0, angleI0, a, t_diff float64) (float64, float64) {
	angleOmegaA_Degree := angleOmegaA0 +
		(180*0.174*(2-2.5*math.Pow(math.Sin(angleI0*math.Pi/180.0), 2)))/(math.Pi*math.Pow(a/EarthRadius, 3.5))*t_diff
	angleOmegaB_Degree := angleOmegaB0 -
		(180*0.174*math.Cos(angleI0*math.Pi/180.0))/(math.Pi*math.Pow(a/EarthRadius, 3.5))*t_diff
	return angleOmegaA_Degree, angleOmegaB_Degree
}

軌道面座標からECI座標系に変換

軌道面上の(u,v)座標は、衛星にとって自然な座標系ですが、地球中心を基準とする座標系（ECI: Earth Centered Inertial）に変換する必要があります。これは、昇交点赤経・軌道傾斜角・近地点引数に基づく3回の座標回転によって実現します。この変換により、地球を中心とした静止基準系での衛星位置を求めることができます。

func transformToEquatorial(u, v float64, angleOmegaA_Rad, angleOmegaB_Rad, angleI0_Rad float64) (float64, float64, float64) {
	elemA := []float64{
		math.Cos(angleOmegaB_Rad), -math.Sin(angleOmegaB_Rad), 0,
		math.Sin(angleOmegaB_Rad), math.Cos(angleOmegaB_Rad), 0,
		0, 0, 1}
	elemB := []float64{
		1, 0, 0,
		0, math.Cos(angleI0_Rad), -math.Sin(angleI0_Rad),
		0, math.Sin(angleI0_Rad), math.Cos(angleI0_Rad)}
	elemC := []float64{
		math.Cos(angleOmegaA_Rad), -math.Sin(angleOmegaA_Rad), 0,
		math.Sin(angleOmegaA_Rad), math.Cos(angleOmegaA_Rad), 0,
		0, 0, 1}
	elemD := []float64{u, v, 0}

	matTempA := mat.NewDense(3, 3, make([]float64, 9))
	matTempC := mat.NewDense(3, 1, make([]float64, 3))
	matA := mat.NewDense(3, 3, elemA)
	matB := mat.NewDense(3, 3, elemB)
	matC := mat.NewDense(3, 3, elemC)
	matD := mat.NewDense(3, 1, elemD)

	matTempA.Mul(matA, matB)
	matTempA.Mul(matTempA, matC)
	matTempC.Mul(matTempA, matD)

	return matTempC.At(0, 0), matTempC.At(1, 0), matTempC.At(2, 0)
}

地球自転を考慮してECEF座標系へ変換

ECI座標系は地球の自転を無視した座標系であり、地上観測には不向きです。実際の地表位置を得るためには、観測時刻に対応する地球自転角（グリニッジ恒星時）を用いて、地球固定座標系（ECEF: Earth Centered Earth Fixed）へ変換する必要があります。これにより、衛星の地球上での位置（例えば緯度・経度上）を正しく把握できるようになります。

func transformToEarthFixed(x, y, z float64, targetTime time.Time) (float64, float64, float64) {
	tmp := time.Date(2006, 1, 1, 0, 0, 0, 0, time.UTC)
	sheta0 := 0.27644444444
	t_diff1 := float64(targetTime.Unix()-tmp.Unix()) / 86400.0
	sheta := sheta0 + 1.002737909*t_diff1

	shetaG_Rad := (sheta - float64(int64(sheta))) * 2.0 * math.Pi

	elemA := []float64{
		math.Cos(-shetaG_Rad), -math.Sin(-shetaG_Rad), 0,
		math.Sin(-shetaG_Rad), math.Cos(-shetaG_Rad), 0,
		0, 0, 1}
	elemB := []float64{x, y, z}

	matA := mat.NewDense(3, 3, elemA)
	matB := mat.NewDense(3, 1, elemB)
	matC := mat.NewDense(3, 1, make([]float64, 3))

	matC.Mul(matA, matB)

	return matC.At(0, 0), matC.At(1, 0), matC.At(2, 0)
}

緯度・経度・高度を求める

ECEF座標が求まれば、最後に衛星の緯度・経度・高度を計算します。これは単純に直交座標を極座標系に変換することで実現します。緯度はZ軸成分から、経度はXY成分から算出し、地心距離から地球半径を引いたものが高度となります。これにより、地球上のどこに衛星が存在するかを直感的に理解できるようになります。
※atanとatan2は似たような関数ですが、引数の与え方が異なるため注意が必要です。実装時にここにハマりました。

func calculateLatLong(x, y, z float64) (float64, float64) {
	fai := math.Asin(z / math.Sqrt(x*x+y*y+z*z))
	lambda := math.Atan2(y, x)
	return rad2deg(fai), rad2deg(lambda)
}

func calculateAltitude(x, y, z float64) float64 {
	return math.Sqrt(x*x+y*y+z*z) - EarthRadius
}

完成コード

今回はGo言語を例にコードと一緒に説明します。コードが長いのでこちらのリポジトリにまとめてあります。

github.com

計算結果

ブログ執筆時点のSTARLINK-1008 (44714 / 2019-074B)の計算をしてみます。緯度・経度・高度・速度ベクトルは下記のように計算されました。
速度は秒速7.3km/sec。とてつもなく早いですね。

hiroyuki@MacBook-Pro starlink % ./starlink
Fetching TLE data for Starlink satellites...!

--- Processing satellite: STARLINK-1008 ---
Found TLE data for STARLINK-1008

Results for STARLINK-1008 at 2025-04-28T17:46:51+09:00:
  Latitude:  32.526199°
  Longitude: -156.440990°
  Altitude:  568.205 km
  Velocity:  7.290 km/s

Processed 1 satellites successfully.


いろいろな衛星の位置計算を行っているサイトの計算結果と比較してみます。誤差はありますが概ね一致することがわかりました。


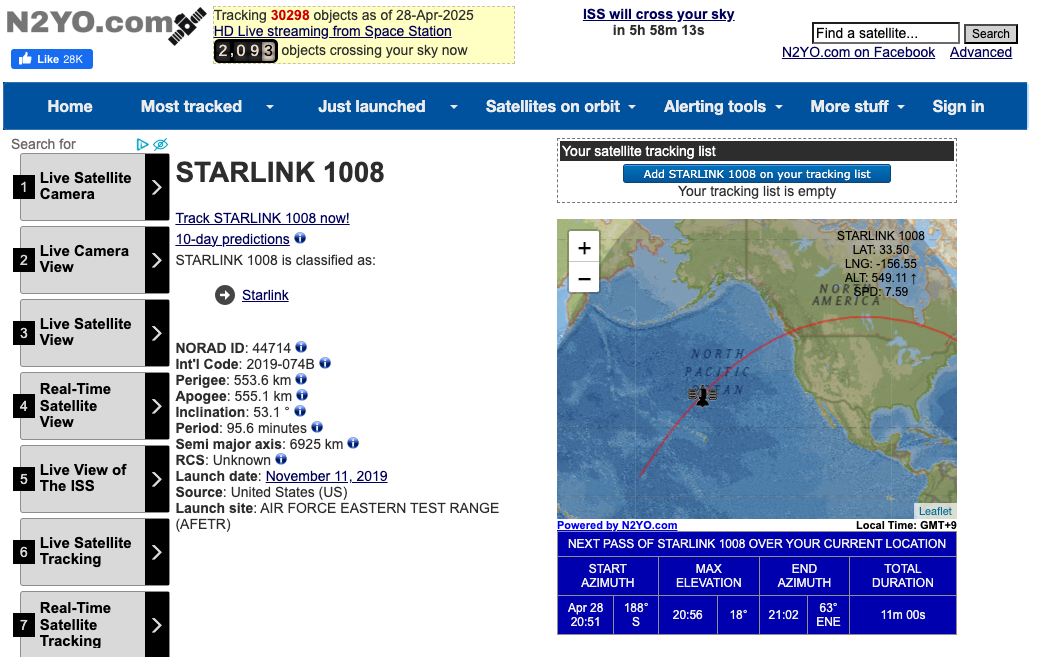
TLEデータとして供給されているStarlink衛星 (7205基)を計算してみます。KMLファイルを出力し、Google Earthに読み込ませてみました。


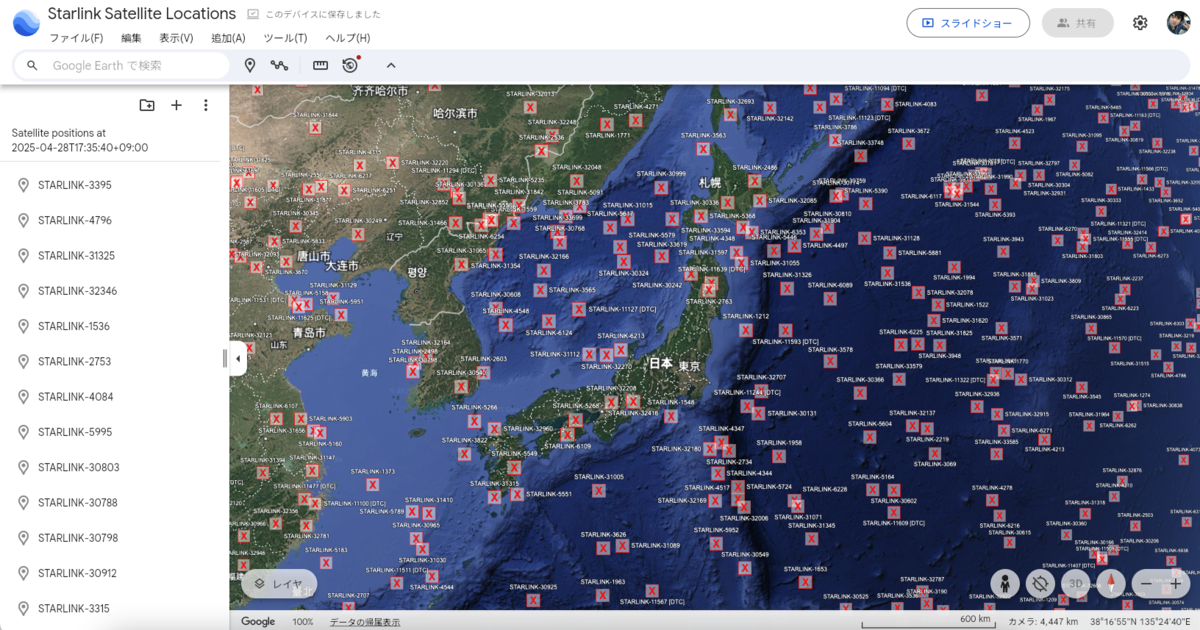
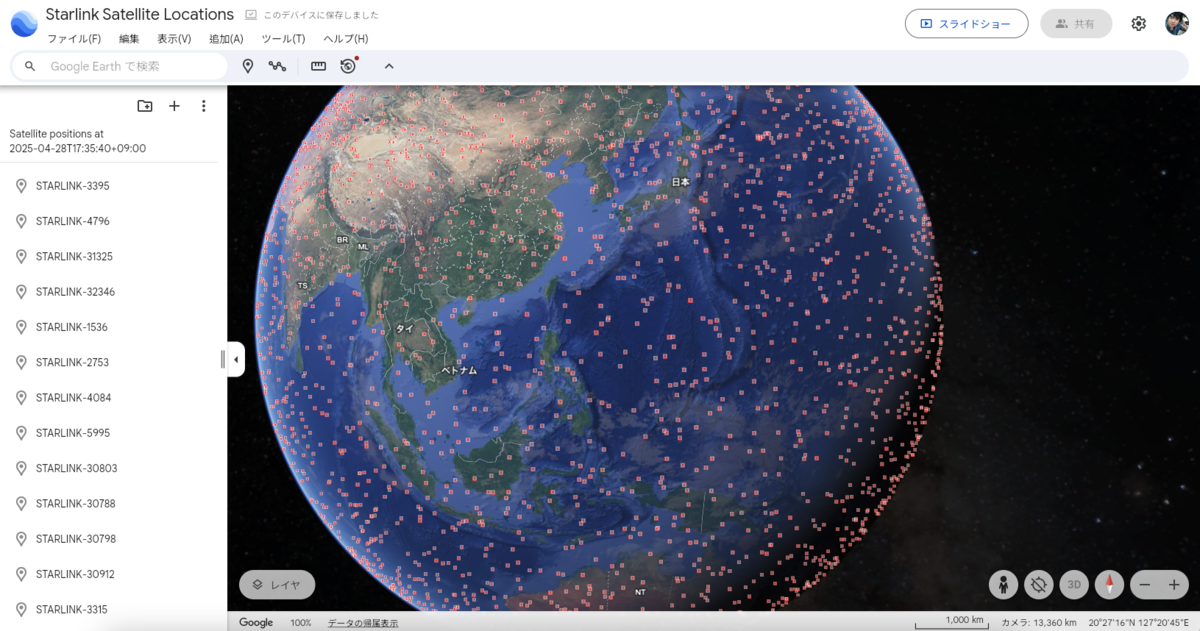
最後に

今回は、Starlinkを例に人工衛星の軌道計算を紹介しました。簡易的な手法で計算しているため、緯度・経度・高度に若干の誤差が生じていることが確認できました。なお、今後の精度向上に向けて、Claude Codeからいくつかアドバイスももらっています。現在は地球を完全な球体と仮定しているなど、まだ改善の余地が多くありそうです。これからも試行錯誤を重ねながら、より精度の高い計算を目指して取り組んでいきたいと思います。

  • 1. 楕円体地球モデルの実装：
    • 現在は球体地球モデル（半径6356.752km）を使用
    • WGS84楕円体モデルを実装（半長軸6378.137km、半短軸6356.752km）
    • 緯度・経度・高度計算を楕円体に対応させる
  • 2. 摂動モデルの強化：
    • 現在はJ2摂動のみ考慮
    • より高次の地球重力場係数（J3、J4など）の導入
    • 第三体摂動（太陽・月）の計算
    • 大気抵抗の考慮（低軌道衛星に重要）
    • 太陽輻射圧の考慮
  • 3. 数値計算の精度向上：
    • ケプラー方程式ソルバーの改善（現在は固定10回反復）
    • 収束判定基準の導入
    • より高精度なニュートン法の初期値設定
  • 4. 座標変換の精度向上：
    • より正確な恒星時計算
    • 極運動の考慮
    • ICRF→ITRFフレーム変換の実装
  • 5. 時間システムの改善：
    • うるう秒の考慮
    • Julian日付計算の実装
    • 地球回転の不規則性を考慮
  • 6. SGP4/SDP4の完全実装：
    • 現在は簡易的なSGP4モデル
    • 完全なSGP4/SDP4アルゴリズムの実装
    • 高精度軌道伝播器（HPOP）の検討

We Are Hiring!

ABEJAは、テクノロジーの社会実装に取り組んでいます。 技術はもちろん、技術をどのようにして社会やビジネスに組み込んでいくかを考えるのが好きな方は、下記採用ページからエントリーください！新卒の方やインターンシップのエントリーもお待ちしております！

※こういうマニアックな技術ネタが好きな人、大歓迎です！

careers.abejainc.com

Page Top
  • Copyright © ABEJA, Inc. All rights reserved.